Corresponding author: ZHANG Yi-min, E-mail: hjneu2007@qq.com
气腿式凿岩机具有高效、低耗的特点,特别适合于铁路、公路、水电等建设施工中使用,也是冶金、煤炭等矿山巷道掘进及各种凿岩作业的常用机械.Tezcan[1]对气动凿岩机活塞断裂表面的微观结构进行了研究,从活塞的硬度、化学成分、金相检验等角度探讨了活塞失效的原因.Lundberg等[2]提出了冲击凿岩系统撞击、凿入和撞击凿入全过程的数值模拟方法,并对世界著名的凿岩机生产商Atlas-Copco公司制造的Cop1038液压凿岩机进行了数值模拟分析与评估.Ajibose等[3]和Franca[4]通过实验和仿真对冲击过程中岩石与冲锤的交互作用和界面力进行了探讨. Ritto等[5]则采用了非参数概率法来考虑岩石的不确定因素对于冲锤所受冲击力的影响.Luciano等[6]建立了冲锤、钎杆和岩石的三自由度有限单元模型.Khulief等[7, 8]通过有限元法分析了钻具钻进的振动特性和动力学特性.Timo等[9]采用有限元方法模拟了钻头与岩石凿入过程.Berzi等[10]从应力波加载后能量耗散的角度对冲击凿岩系统的非线性动力学进行了分析.詹军等[11]利用ANSYS软件对气动冲击器的活塞进行了非线性有限元分析.而鉴于实际工程中活塞和钎杆的结构形状复杂,上述文献采用的有限元模型和数值方法多针对简化后的规则形状杆件碰撞,很难反映出冲击系统的真实碰撞情况.近几年,由于先进有限元方法已经发展成熟,本文应用通用有限元分析软件ANSYS/LS-DYNA,分析了气腿式凿岩机活塞的应力、应变,完全模拟出活塞反复撞击钎杆全过程的应力、应变变化状况,并通过实验验证了结果的正确性.该分析结果为今后结构的改进、材料和加工工艺的选择提供理论依据.
1 冲击系统力学模型该冲击系统主要由活塞和钎杆组成,工作原理为活塞以较高的速度和频率撞击钎杆,在这个过程中能量以应力波的形式传递给钎杆,通过钎杆使工作介质发生变形或破坏,应力波的形状和大小取决于活塞的结构和冲击末速度.一般在进行钻凿极坚硬岩石数值模拟研究时,假设钎杆一端为固定端,其力学模型如图 1所示.
 | 图 1 冲击系统动力学模型Fig. 1 Dynamical model of impact system |
活塞冲击末速度指活塞冲程终了,其冲击钎尾时的瞬时速度,其与凿岩机结构参数和压气压力关系的计算公式[12]为

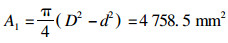 ;s为活塞结构行程,文中取值60 mm;m为活塞质量,文中取值1.863 kg.
3 活塞的有限元分析
3.1 建立有限元模型
;s为活塞结构行程,文中取值60 mm;m为活塞质量,文中取值1.863 kg.
3 活塞的有限元分析
3.1 建立有限元模型
气腿式凿岩机活塞的结构如图 2所示,钎杆选用GB/T6481—2002中22*108钎杆.冲击系统的基本参数如表 1所示.
 | 图 2 活塞结构示意图Fig. 2 Structure diagram of piston |
| 表 1 冲击系统基本参数Table 1 Basic parameters of impact system |
根据整个冲击系统的结构和受力状况,活塞和钎杆均为轴对称结构,取系统的一半进行分析.将几何模型适当简化倒角后,导入ANSYS有限元软件中并采用实体单元SOLID164进行单元网格划分.由于LS-DYNA求解器对于有限元模型的网格质量要求较高,网格划分过程中尽量采用六面体划分.系统被划分成79 453个单元、49 924个节点,有限元模型如图 3所示.
 | 图 3 有限元模型Fig. 3 Finite element model(a)—活塞; (b)—冲击系统. |
活塞在冲程和回程的大部分工作时间内受压气作用,但在与钎杆发生碰撞时受到的冲击力远大于压气对活塞的作用力.因此,活塞与钎杆在极短时间内碰撞的动力学特性是本文研究的主要内容.
为了模拟活塞的实际工况,在钎杆顶端施加约束,限制钎杆所有的自由度运动,此外,在钎杆和活塞对称面内施加对称约束(即约束沿y轴的移动方向自由度及绕x,z轴的转动方向自由度).分析时设定活塞离钎杆5 mm,给活塞施加一个初速度8.754 m/s(即上文中提到的活塞冲击末速度),不考虑摩擦力,采用LS-DYNA求解器对系统进行动力学特性求解.整个分析时间取 4 ms.在钎杆内,钢中的声速c=5 080 m/s,应力波在钎杆内的传播时间t=2 308×1 000/5 080 000=0.45 ms,所以计算中的时间步长必须小于该时间的1/20,取0.01 ms.
3.3 计算结果及分析图 4为活塞速度随时间的变化曲线,由此可知活塞与钎杆在0.57 ms时开始碰撞,1.64 ms时活塞开始回弹,结束碰撞.图 5为碰撞过程中活塞和钎杆的受力云图,在整个冲击过程中,0.63 ms时活塞承受最大应力为827 MPa,最大应力位于碰撞面上内孔倒角处;而钎杆的最大应力则发生在1.08 ms时的钎尾处(1 450 MPa).
 | 图 4 活塞速度曲线Fig. 4 Velocity curve of piston |
 | 图 5 应力云图Fig. 5 Stress nephogram(a)—0.63 ms,活塞; (b)—1.08 ms,冲击系统. |
由上述分析可知,对于活塞,撞击端面的应力最大,花键根部受力也不可忽视.图 6为活塞撞击端面和花键根部的应力随时间的变化曲线.活塞承受的最大应力小于活塞的屈服极限,而大于材料的疲劳极限,因此,活塞不会因为一次碰撞冲击导致端面塑性变形或者杆身断裂.活塞的失效形式很可能为花键根部疲劳断裂破坏或撞击面凹陷疲劳破坏(一般认为凿岩机的活塞撞击端面下凹2 mm即废弃),计算结果与工程实际情况吻合.
 | 图 6 活塞的应力曲线Fig. 6 Stress curves of piston(a)—活塞撞击端面; (b)—活塞花键根部. |
为验证分析结果的正确性,将分析结果与Atlas-Copco沈阳建筑矿山设备有限公司提供的实验结果进行对比.在实验中,根据GB5621/T—2008,采用应力波法测量YT29A气腿式凿岩机冲击能,结果为73.562 J.在有效应力波(无反射波影响的入射波视为有效应力波)0.25 ms内距离钎尾40 mm处钎杆应力随时间变化曲线如图 7所示.由该应力曲线计算活塞的冲击能:

 | 图 7 钎杆测试处的应力曲线Fig. 7 Stress curve at drill rod test position |
由上述分析可知,实验结果与仿真结果的误差为3.59%,在一定程度上证明了仿真结果的正确性.
4 结论本文以气腿式凿岩机活塞为研究对象,根据实际工况建立了活塞和钎杆冲击系统的有限元模型.利用ANSYS/LS-DYNA软件对其进行了非线性有限元分析,比较了活塞冲击能的计算结果与实验结果,验证了计算结果的准确性.通过分析活塞与钎杆碰撞过程中的应力应变情况,可知活塞的失效形式可能为花键根部疲劳断裂破坏或撞击面凹陷疲劳破坏,与实际情况十分吻合.针对这种失效形式,可从活塞的材料学、热处理工艺等方面进行改进,提高活塞的使用寿命.
| [1] | Tezcan S.Failure study of pneumatic rock drill piston[J].Engineering Failure Analysis,2006,13(7):1108-1115.( 1) 1) |
| [2] | Lunberg B,Carlsson J.Analysis of elastic wave in non-uniform rods from two-point strain measurement[J].Journal of Sound and Vibration,1990,137(3):483-493.( 1) 1) |
| [3] | Ajibose O K,Wiercigroch M,Akisanya A R.Experimental studies of the resultant contact forces in drill bit-rock interaction[J].International Journal of Mechanical Sciences,2015,91:3-11.( 1) 1) |
| [4] | Franca L F P.A bit-rock interaction model for rotary percussive drilling[J].International Journal of Rock Mechanics & Mining Sciences,2011,48(5):827-835.( 1) 1) |
| [5] | Ritto T G,Soize C,Sampaio R.Non-linear dynamics of a drill-string with uncertain model of the bit-rock interaction[J].International Journal of Non-linear Mechanics,2009,44(8):865-876.( 1) 1) |
| [6] | Luciano E C,Dante A E.A 3D FEM methodology for simulating the impact in rock-drilling hammers[J].International Journal of Rock Mechanics & Mining Sciences,2008,45(5):701-711.( 1) 1) |
| [7] | Khulief Y A,Al-Naser H.Finite element dynamic analysis of drill-strings[J].Finite Elements in Analysis and Design,2005,41:1270-1288.( 1) 1) |
| [8] | Khulief Y A,Al-Sulaiman F A,Bashmal S.Vibration analysis of drill-strings with self excited stick-slip oscillations[J].Journal of Sound and Vibration,2007,299(3):540-558.( 1) 1) |
| [9] | Timo S,Dmitri G,Mikko H,et al.Numerical and experimental study of percussive drilling with a triple-button bit on Kuru granite[J].International Journal of Impact Engineering, 2014,72:56-66.( 1) 1) |
| [10] | Berzi P,Beccu R,Lundberg B.Identification of a percussive drill rod joint from its response to stress wave loading[J].International Journal of Impact Engineering,2014,18(3):281-290.( 1) 1) |
| [11] | 詹军,殷琨,于清杨,等.气动冲击器活塞的非线性有限元分析[J],矿山机械,2003,31(321):7-9,(Zhan Jun,Yin Kun,Yu Qing-yang,et al.Nonlinear finite element analysis of piston of pneumatic DTH hammer[J].Mining & Processing,2003,31(321):7-9.)( 1) 1) |
| [12] | 张玉成.凿岩机械讲座介绍和气动凿岩机参数计算[J].凿岩机械气动工具,2000(2):6-14.(Zhang Yu-cheng.Drilling machine introduction and pneumatic rock drill parameters computation[J].Mechanical Pneumatic Rock Drill Tools,2000(2):6-14.)( 1) 1) |




