Corresponding author: LIU Xin-rui,E-mail: liuxinrui@ise.neu.edu.cn
多机电力系统的气门开度控制对提高电力系统稳定性具有至关重要的作用,多机电力系统是由一系列带有互联项的子系统组合的非线性系统[1, 2, 3].Takagi-Sugeno (T-S)模糊模型用于逼近复杂非线性系统并进行控制具有很好的效果,国内外许多学者基于T-S模糊模型对互联系统的分散控制综合和分析方法进行了深入研究[4, 5, 6].文献[7]针对一类带有参数不确定性的多机电力系统设计了分散鲁棒控制器,给出了系统稳定的条件.而当系统状态不完全可测时,需要设计基于观测器的状态反馈控制器,但已有文献不可避免地都会出现非线性矩阵不等式(non-LMIs)的结果.为求解non-LMIs,文献[8]给出了基于观测状态的两步走的控制器设计方法,文献[9]采用基于遗传算法的寻优设计,但都不可避免地带来结果的保守性.文献[10]在H∞性能指标下研究不确定性系统的控制器设计问题,得到使闭环系统稳定且满足一定的动态性能的充分条件.
本文研究了汽轮发电机组成的多机电力系统气门开度的模糊观测分散控制器的设计问题,提出了仅需一步就能求解的LMIs条件,减小了采用传统两步法求解所带来的保守性.
1 问题描述考虑通过输电线连接的N台非中间再热式汽轮发电机组成的多机电力系统的气门开度控制问题,定义第i台发电机的状态向量为xi(t)=[Δδi(t)Δwi(t)ΔPMi(t)ΔXEi(t)]T,其中,转子角增量Δδi(t)=δi(t)-δi0,相对角速度Δwi(t)=wi(t)-w0,机械功率增量ΔPMi(t)=PMi(t)-PMi0,气门开度增量ΔXEi(t)=XEi(t)-XEi0,则每台发电机的状态方程描述为

根据式(1),建立其T-S模糊模型为

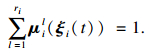
根据并行分布补偿策略,采用模糊控制器:

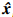 i(t)为观测状态.
i(t)为观测状态.
考虑如下模糊观测器估计多机系统的状态:

其中Lil是第l条观测规则的观测增益,且 i(t)=
i(t)=
定义系统的误差为

由式(2),(4)和(5)可以得到:


其中: ,
, .
.
定理1 对于给定干扰γi>0,i=1,…,N,如果存在矩阵Kil,Lil,对称正定矩阵Xi,Yi,对称矩阵Xilm,m>l,l,m=1,…,ri,满足矩阵不等式(8)~(10),则式(3)和(4)使模糊互联系统(2)稳定且满足H∞性能指标γi.



其中:

证明:选择Lyapunov函数
 ,对其求导得
,对其求导得
 ,当wi≡0时,
,当wi≡0时,
 ,即闭环系统渐近稳定.当wi≠0时,
,即闭环系统渐近稳定.当wi≠0时,  ,当x(0)=0时,
V(x(0))=0,得
,当x(0)=0时,
V(x(0))=0,得  ,定理1得证.
,定理1得证.
注1:定理1不是基于线性矩阵不等式(LMIs)的,只能由常规的两步法求解,且两步法的LMIs条件仅是定理1的充分条件.定理2给出了一种单步求解LMIs的条件,且该条件是定理1的充分必要条件.这克服了定理1中两步法求解带来的保守性.
定理2 对于给定干扰γi>0,i=1,…,N,如果存在对称正定矩阵  ,对称矩阵
,对称矩阵  ,Pilm,Qilm,Pill,Qill,m>l,l,m=1,…,ri满足LMIs(11)~(16),则式(3)和(4)使模糊互联系统(2)稳定且满足H∞性能指标γi.
,Pilm,Qilm,Pill,Qill,m>l,l,m=1,…,ri满足LMIs(11)~(16),则式(3)和(4)使模糊互联系统(2)稳定且满足H∞性能指标γi.






其中:

证明略.
注2:考虑系统建模误差、工况变化、故障及干扰等情况引起的系统参数不确定性情况,利用定理1和定理2的推导方法也可得到类似的结论.
3 仿真选取文献[11]中的两机无穷大母线电力系统及其系统参数,系统包含3台发电机,1#发电机和2#发电机分别通过变压器T1和T2接入无穷大母线,以3#发电机作为参考.
采用局部线性化方法对多机气门开度控制系统建立T-S模糊模型,系统矩阵为


利用Matlab的Lmiedit工具箱,求解得

给定初值x1(t)=x2(t)=[1 1 1 1]T及扰动w1(t)=sin(2πt),w2(t)=cos(2πt),系统输出见图 1,观测误差曲线见图 2~3.
 | 图 1 1#和2#发电机的输出曲线 Fig. 1 Outputs of 1# and 2# generator |
 | 图 2 1#发电机的观测误差曲线 Fig. 2 Observer errors of 1# generator |
 | 图 3 v Fig. 3 Observer errors of 2# generator |
本文研究了汽轮发电机组成的多机电力系统气门开度的基于观测状态的分散控制器的设计问题.基于T-S模糊模型给出了多机电力系统具有H∞性能指标的条件,该基于LMIs的条件仅需一步就能求解,减小了采用传统两步法求解的保守性.仿真结果验证了其有效性.
| [1] | Siljak D D.Large scale dynamical systems:stability and structure[M].New York:North-Holland,1978:35-40.( 1) 1) |
| [2] | He C,Li J,Zhang L.Decentralized adaptive control of nonlinear large-scale pure-feedback interconnected systems with time-varying delays[J]. International Journal of Adaptive Control and Signal Processing, 2013,2(10):103-109.( 1) 1) |
| [3] | Koo G B,Park J B,Joo Y H.Robust decentralized control for fuzzy large-scale systems using dynamic output-feedback[C]//2013 American Control Conference.Washington,DC,2013:6412-6417.( 1) 1) |
| [4] | Hsiao F H,Chen C W,Liang Y W,et al.T-S fuzzy controllers for nonlinear interconnected systems with multiple time delays[J].IEEE Transactions on Circuits and Systems,2005,52(9):1883-1893.( 1) 1) |
| [5] | Wang W J,Lin W W.Decentralized PDC for large-scale T-S fuzzy system [J].IEEE Transactions on Fuzzy Systems,2005,13(6):779-786.( 1) 1) |
| [6] | Liu X D,Zhang Q L.New approaches to H∞ controller designs based on fuzzy observers for T-S fuzzy systems via LMI[J].Automatica,2003,39:1571-1582.( 1) 1) |
| [7] | Wang Y Y,David J,Guo G X.Robust decentralized control for multimachine power systems[J].IEEE Transactions on Circuits and System,1998,45(3):271-279.( 1) 1) |
| [8] | Lo J C,Lin M L.Observer-based robust H∞ control for fuzzy systems using two-step procedure[J].IEEE Transactions on Fuzzy Systems,2004,12(3):350-359.( 1) 1) |
| [9] | Tseng C S.A novel approach to H∞ decentralized fuzzy-observer-based fuzzy control design for nonlinear interconnected systems[J].IEEE Transactions on Fuzzy Systems, 2008,16(5):1337-1350.( 1) 1) |
| [10] | Wu J L.Robust H∞ control for polytopic nonlinear control systems [J].IEEE Transactions on Automatic Control, 2013,58(11):2957-2962.( 1) 1) |
| [11] | 孙妙平,年晓红,潘欢.基于观测器的汽轮发电机气门开度的时滞无关控制[J].控制理论与应用,2012,29(5):593-598.(Sun Miao-ping,Nian Xiao-hong,Pan Huan.Observer-based delay-independent control for steam valves of steam turbo-generator[J].Control Theory & Applications, 2012,29(5):593-598.)( 1) 1) |




