可靠性分配是根据一定的原则和方法，将系统可靠性指标自上而下逐级分配到下属各级产品的过程^[1].国外的可靠性分配理论^[2]在20世纪就开始被大范围地研究，现已应用到各个领域，文献^{[3, 4]}介绍了可靠性分配在汽车、软件领域内的相关应用.在机械系统可靠性分配工程中，各种分配方法被引入其中.文献^{[5, 6, 7]}分别将 模糊评分法、模糊层次分析法和遗传算法引入可靠性分配中以考虑多种影响因素，但其中的专家评分必然会存在一定的主观性；文献^[8]提出了一种基于神经网络的分配法，但需要大量实验数据进行训练.

为提出一种容易操作、施行效果较好、能较好解决机械系统可靠性再分配问题的方法，本文提出了一种基于机床故障信息的可靠性模糊分配方法.鉴于影响机床可靠度的因素较多且关系复杂，难以用经典数学加以描述，故引入模糊理论，建立模糊分配模型，经熵权法加权得到整机故障率分配系数以指导机床可靠性指标的再分配.

经现场调研并查阅此系列机床的售后维修记录，对机床整机故障间隔时间进行预处理，去除磨合期内的故障数据和人为操作不当引起的故障数据后，共计550条故障信息，其分布直方图见图 1.可以看出，该系列机床故障间隔时间大约有一半数据分布在1000h以下，查阅国外机床资料可知其平均故障间隔时间MTBF(mean time between failures)值一般在1500h左右，可见国产机床与国外机床还有很大差距.按国外机床标准，初定该机床整机MTBF目标值为1500h，整机可靠度达到0.99.

图 1(Figure 1)

Fig. 1

图1 故障数据分布直方图 Fig. 1 Histogram of failure data

选取两参数Weibull分布、对数正态分布、最小极值分布和正态分布四种分布对整机故障数据进行拟合得到模型分布图，见图 2.各分布图相关系数分别为0.994，0.963，0.943，0.979.由于Weibull分布的相关系数最大，故认为机床整机故障间隔时间数据符合两参数的Weibull分布.

图 2(Figure 2)

Fig. 2

图2 模型概率分布图 Fig. 2 Probability distribution of model (a)—Weibull分布； (b)—对数正态分布； (c)—最小极值分布； (d)—正态分布.

采用极大似然估计法进行分布模型的参数估计.设Weibull分布的概率密度函数为f(t_i;α,β)，对故障数据t_i的似然函数L求对数后，得到函数ln L，再对α，β分别求偏导数后令其为零，可得

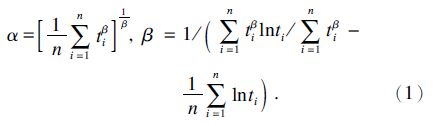
求出分布函数的参数估计值后，应进行假设检验.本文采用皮尔逊χ²检验法^[9]进行拟合检验.首先，将故障数据分成17组，计算频数v_i、理论频数np_i(p_i为理论频率)等参数，得，其中数据总量n=550.然后，取显著性水平为0.005，查χ²分布表得对应自由度17-1-2=14的临界值为χ_0.995²(14)=31.319，由于4.654＜χ_0.995²(14)，故接受原假设，即认为故障间隔时间数据服从两参数为α=1395.7,β=1.1646的Weibull分布.

Weibull分布函数W(t)就是失效概率函数，所以到此建立了整机故障间隔时间的可靠度函数：

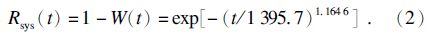
本文中的数控机床是基于模块化生产的，在考虑故障类别和功能模块的基础上，对整机故障数据进行分类，得到10个子系统，见表 1.对各子系统的故障数据进行类似整机可靠度函数的参数计算后，可得各子系统故障间隔时间的可靠度函数.对子系统可靠度函数采用检验法进行假设检验，检验结果均可接受，得到具体的子系统可靠度函数见表 1.

表1

Table 1

表1(Table 1)

表1 子系统故障间隔时间可靠度函数 Table 1 Subsystem’s reliability functions 序号 系统 故障间隔时间可靠度函数表达式 相关系数 1 基础 RB(t)=exp[-(t/2212.4)1.6993] 0.987 2 传动 RT(t)=exp[-(t/2157.8)1.3739] 0.985 3 进给 RF(t)=exp[－(t/3184.8)1.7069] 0.956 4 刀架 RK(t)=exp[－(t/1971.0)1.2691] 0.982 5 装夹 RG(t)=exp[－(t/2415.7)1.5017] 0.949 6 数控 RN(t)=exp[－(t/2410.2)2.2501] 0.984 7 液压 RH(t)=exp[－(t/2279.9)1.2946] 0.987 8 排屑 RR(t)=exp[－(t/1827.4)1.2152] 0.999 9 冷却 RC(t)=exp[－(t/2066.2)1.3727] 0.993 10 润滑 RF(t)=exp[－(t/2435.2)2.1227] 0.985

表1 子系统故障间隔时间可靠度函数 Table 1 Subsystem’s reliability functions

鉴于篇幅问题，本文只给出相关系数最小的装夹系统的故障数据分布拟合性检验过程.装夹系统故障数据总量n₅= 57，分成7组，得$\sum\limits_{i = 1}^7 {\left( {\frac{{v_i^2}}{{{n_5}{p_i}}}} \right) - {n_5} = 10.926}$，i∈[1, 7].取显著性水平为0.005，查χ²分布表得对应自由度7-1-2= 4的临界值为χ_0.995²(4)=14.860，由于10.926＜χ_0.995²(14)，故接受原假设，认为装夹系统故障间隔时间数据服从两参数为α=2415.7,β=1.5017 的Weibull分布.

图 3为机床整机和子系统随工作时间的可靠度函数曲线.由图可知，整机的可靠度总是低于各子系统可靠度，排屑系统的可靠度最低，可见由故障信息统计得到的可靠度曲线符合该机床的工程实际.

图 3(Figure 3)

Fig. 3

图3 整机/子系统的可靠度曲线 Fig. 3 Curves of systems’/subsystems’ reliability

故障次数比重比f_i定义为子系统i故障次数占整机故障次数总和的比重.某子系统f_i值越小，说明该系统越不容易出现故障，应分配给较低的故障率.

整机故障次数共550次，各子系统故障次数分别为54，38，42，60，57，11，61，128，84，15，由此可得各子系统(按表 1所示序号)的故障次数比重比{f_i|i=1,…,10 }={ 0.0982，0.0691，0.0764，0.1091，0.1036，0.0200，0.1109，0.2327，0.1527，0.0273}. 很明显，排屑系统的故障比重比较大，是整机的薄弱环节，应分配给较高的故障率.

故障维修停时比重比r_i定义为子系统i每次故障的平均维修停时占整机故障平均维修停时的比例.经计算， {r_i|i=1,…,10}={0.0452，0.0412，0.0762，0.2507，0.0415，0.0567，0.0494，0.3603，0.0378，0.0410}.

故障维修停时比重比值越大说明该子系统发生故障时平均维修停时越长，则该故障对生产造成的停时影响越大，故应尽量分配给相对较低的故障率，以减少机床工作期间因故障产生过长的维修停时.由r_i可知，排屑系统的故障维修停时比重比较大，说明维修性较差，故应分配给较低的故障率.

机械系统可看作串联系统，可靠度数学模型为

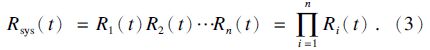
定义可靠度影响度为

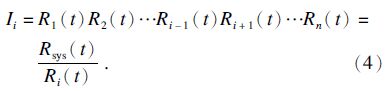
可靠度影响度表征了子系统可靠度对整机可靠度的影响程度，若某子系统I_i值较大，说明其可靠度对整机可靠度的影响较大，应着力提高该子系统的可靠度，降低故障率.

将整机和各子系统的可靠度函数代入式(4)便可求得t=1500h时的子系统可靠度影响度 {I_i|i=1,…,10}=[0.5650，0.6183，0.4444，0.6836，0.5496，0.4754，0.6029，0.7402，0.6419，0.4819]. 易知，刀架系统可靠度影响度较大，则该子系统对整机故障率影响度较大，故应分配给较低的故障率.

定义子系统结构复杂度为每个子系统的组件数占整机组件数的比例，即

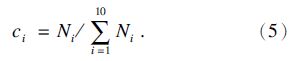
分配可靠性指标时应考虑子系统的复杂度，机构复杂的子系统应分配给较低的MTBF.

在实际机床可靠性分配过程中，本文考虑了以上4种故障影响因素，鉴于很难用确定的函数式或概率统计方法表达出具体的分配模型，本文引入模糊数学理论来建立可靠性指标的分配模型^{[9, 10]}.

设影响因素集 K ={k₁,k₂,k₃,k₄}={故障次数比重比，维修停时比重比，可靠度影响度，结构复杂度}.

首先建立针对影响因素k₁的对比矩阵 S:

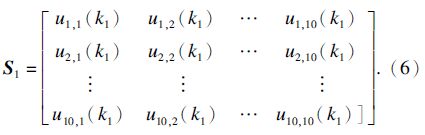
同理，由式(6)可得到各子系统针对其他三个影响因素的对比矩阵 S₂，S₃，S₄ .

定义子系统i对影响因素k₁的隶属度为，代入数据得到各子系统对影响因素k₁的隶属度向量：

M₁=(u_i(k₁))=[ 0.4619，0.5407，0.5183 0.4384，0.4499，0.7812，0.4347，0.2803，0.3649，0.7296].

同理可求得其他三个因素的隶属度向量分别为:

M₂=(u_i(k₂))=[0.5829，0.6032，0.4670，0.2379，0.6016，0.5325，0.5632，0.1856，0.6219，0.6043]；

M₃=(u_i(k₃))=[0.5036，0.4812，0.5629，0.4564，0.5104，0.5463，0.4874，0.4368，0.4719，0.5430]；

M₄=(u_i(k₄))=[0.6158，0.4590，0.3214，0.2324，0.3846，0.5403，0.5753，0.5948，0.6382，0.6382].

熵权法是一种较客观的、能保留较多原始信息的求权法，本文用其求解子系统对各影响因素的相对隶属度向量的权重，经加权得可靠度综合影响度.

首先形成决策矩阵 M₀=[M₁,M₂,M₃,M₄] ^T，对矩阵元素进行标准化处理m_li=, 得到标准化矩阵 M_s=[M_s,1,M_s,2, M_s,3,M_s,4]^T，计算熵值 E_l=，计算各因素权重,得到如下权重: w₁=0.2482,w₂=0.2445,w₃=0.2590,w₄=0.2483，则可靠度综合影响度加权公式为

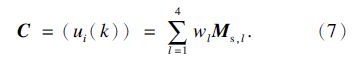
将权重和隶属度向量代入式(7)得子系统对整机可靠度的综合影响度 C =[0.5405，0.5203， 0.4684，0.3429，0.4865，0.5998，0.5147，0.3758，0.5233，0.6279].

按文献^[10]可得机床故障率分配模型为λ₁∶ λ₂∶ … ∶ λ₁₀=u₁(k)∶ u₂(k)∶ … ∶ u₁₀(k).若机床可靠性分配指标(即MTBF值)为 1500h，则整机故障率λ_s=1/1500，各子系统故障率λ_i的分配公式为

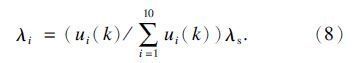
将向量 C 代入式(8)得各子系统故障率分配值：{λ_i}={0.7207，0.6937，0.6246，0.4572，0.6486，0.7997，0.6862，0.5010，0.6977，0.8372}×10^-4 h^-1.

由公式MTBF_i=1/λ_i得

MTBF_i=[13876，14415，16011，21871，15418，12505，14572，19960，14332，11944] h

分配后，由R_i=1－λ_i求各子系统的可靠度，分配前后MBTF值和可靠度对比如表 2所示.从中可明显看出，若要提高整机系统的可靠性，必须着力提高可靠性较差的刀架系统和排屑系统的可靠度，这与进一步提高可靠度较高的子系统相比是相对容易的.

表2

Table 2

表2(Table 2)

表2 平均故障间隔时间和可靠度 Table 2 MTBF and reliability 子 系 统 分配前 分配后 MTBF/h R MTBF/h R 基础系统 1974 0.5965 13876 0.99992 传动系统 1973 0.5451 14415 0.99993 进给系统 2841 0.7584 16011 0.99994 刀架系统 1830 0.4931 21871 0.99995 装夹系统 2181 0.6133 15418 0.99994 数控系统 2135 0.7090 12505 0.99992 液压系统 2107 0.5590 14572 0.99993 排屑系统 1714 0.4553 19960 0.99995 冷却系统 1889 0.5250 14332 0.99993 润滑系统 2156 0.6994 11944 0.99992

表2 平均故障间隔时间和可靠度 Table 2 MTBF and reliability

假设各子系统均为独立串联系统，当整机MTBF=1500h时，其可靠度为0.9993.但事实上，机床系统内部关系较复杂，子系统间并非完全独立串联关系，实际为相关系统，即各子系统失效为相容事件.由独立事件和相容事件的概率加法公式知，在各子系统失效率不变的情况下，子系统为独立串联关系的整机失效率比子系统为相关关系的整机失效率要大，故子系统独立串联的整机系统可靠度比子系统为相关关系的整机系统可靠度要小.所以，若按本文方法分配故障率，分配后的机床整机可靠度应大于0.9993，满足设计目标R_s=0.99.

本文基于数控机床的实际工作故障信息，建立了系统可靠度模型，充分考虑了多种可靠度分配影响因素，引入模糊数学知识和熵权法建立了机电液复杂系统可靠度的模糊分配模型.基于实际的产品工作故障数据，本方法较其他评分分配法包含了更多的产品故障信息，更具实用性，对复杂机电液系统的可靠性再分配和产品可靠性的改善有较大指导意义.