Corresponding author: HUANG Xian-zhen, associate professor, E-mail: xzhhuang@mail.neu.edu.cn
近年来,国内外学者对金属切削的基本理论与方法进行了深入研究和广泛探讨,建立了多种金属切削物理力学模型,试图提出一种有效的金属切削过程热力耦合模拟分析方法,用以准确描述金属切削过程中材料的去除机理.根据金属切削变形区性质的不同,金属切削物理力学模型大体上可以分成两类:单一平面剪切区模型[1]和平行平面剪切区模型[2, 3].总体来说,平行面剪切模型的构建与求解过程要比单一面剪切模型复杂得多,但平行面剪切区模型在推导过程中考虑了材料的加工硬化和热软化效应,与金属切削实验的结果吻合得更好.因此,平行平面剪切区模型得到了更加广泛的关注和系统深入的研究,其理论体系也相对较为完善;不足之处是,在金属切削力预测过程中,设计人员通常将切削参数信息视为精确、无误差的,而在实际工程问题中,可以完全、精确描述的信息因素却是极少的,大部分因素都是非完全、非精确的[4].这种信息的不完全和不精确性可以称为不确定性.比如,在机床制造过程中,加工和装配误差会造成几何尺寸的不确定性;在金属切削过程中,工作环境中的偶然因素会使荷载及工程材料的力学性能具有不确定性.显而易见,上述不确定因素是工程实际中所固有的,对金属切削有着不可忽视的影响.确定性模型忽略了不确定因素对金属切削过程的影响,势必会造成一定的分析误差.因此按照确定性设计方法设计出来的切削方案,在工程应用中很可能会出现性能偏差,往往难以实现预期的效果(如刀具磨损严重、加工误差过大、加工面划伤等).本文综合考虑随机因素对金属切削过程的影响,采用蒙特卡罗数值模拟方法,研究金属切削过程中切削力的统计分布规律.
1 剪切区模型如图 1所示,采用非等分平行面剪切区模型建立直角切削剪应变、剪应变率以及剪切方向速度预测理论.直角切削可以看作是二维切削.在稳态切削过程中,切屑速度是坐标y的函数,所以剪切区的材料速度分量为
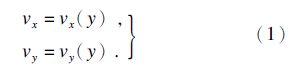

|
图1 不等分剪切区模型 Fig. 1 Model of unequally divided shear-zones v:切削速度; vc:切屑速度; vs:切屑的剪切速度;a:切削厚度; γ0:前角; h: 剪切区厚度; k: 不等分系数 |
根据运动关系,在两个边界处(始剪切线CD和终剪切线EF)的法向速度分量为
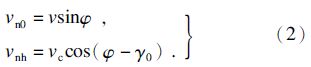
根据塑性不可压缩条件,可知通过剪切区的法向速度是常数(vn0=vnh),所以由式(2)可得切屑速度为
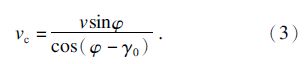
由相容条件可得剪应变率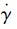 和速度的关系为
和速度的关系为
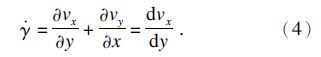
根据剪应变率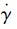 是剪应变γ的随体导数,可得
是剪应变γ的随体导数,可得
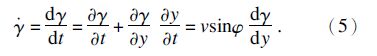
目前,通过理论推导获取剪应变率函数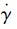 还比较困难,主要根据实验结果假设适当的函数表达式用以表征剪应变率.实验表明
还比较困难,主要根据实验结果假设适当的函数表达式用以表征剪应变率.实验表明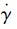 在始剪切和终剪切处的值趋近于零,而在主剪切面处达到最大值[5, 6].针对这一实验现象,国内外研究人员提出多种剪应变率分布假设模型.其中,文献[7]提出的剪应变率的分段幂律分布假设与实验结果吻合较好.本文采用该模型确定剪应变率.
在始剪切和终剪切处的值趋近于零,而在主剪切面处达到最大值[5, 6].针对这一实验现象,国内外研究人员提出多种剪应变率分布假设模型.其中,文献[7]提出的剪应变率的分段幂律分布假设与实验结果吻合较好.本文采用该模型确定剪应变率.
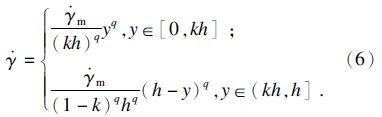
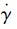 m为最大剪应变率;h为剪切区厚度;k为不等分系数;q用以描述切向速度的非一致分布特性,低速时取q=3,高速时取q=7.
m为最大剪应变率;h为剪切区厚度;k为不等分系数;q用以描述切向速度的非一致分布特性,低速时取q=3,高速时取q=7.
联立方程(5)和(6)对y积分,并考虑到在始剪切线处的应变等于零的边界条件,可得到速度与应变的关系:
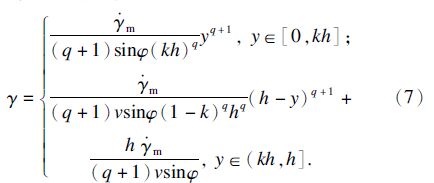
联立方程(5)和(7),并考虑切向速度分量在始剪切线和终剪切线处的边界条件,对y积分得
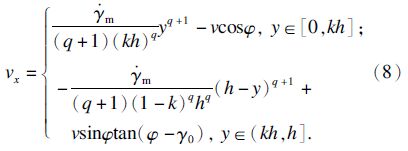
主剪切平面的切向速度分量等于零[6],所以

求解方程(9),可得不等分系数k和最大剪切应变率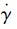 m分别为
m分别为
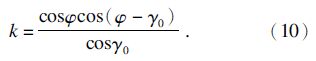
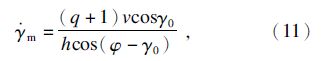
把式(10)和(11)代入式(6)~(8)中,就可得到剪应变率、剪应变和剪切速度关于坐标y的函数.
2 剪切区控制方程 2.1 材料控制方程为了从金属切削过程的仿真分析中得到有效的 分析结果,首先要确定工件材料的属性.在切削条件下,材料屈服流动行为的描述较常采用Johnson-Cook(JC)本构关系模型.工件切削的剪应力τ的表达式为
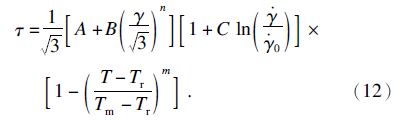
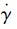 为剪应变率;
为剪应变率;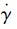 0为参考剪切应变率;Tr为待加工零件的初始温度(通常为加工车间的环境温度);Tm为工件材料的融点;C为应变率敏感系数(黏性);n为硬化指数;m为热软化指数;T为切削加工过程中工件的表面温度.
2.2 温度控制方程
0为参考剪切应变率;Tr为待加工零件的初始温度(通常为加工车间的环境温度);Tm为工件材料的融点;C为应变率敏感系数(黏性);n为硬化指数;m为热软化指数;T为切削加工过程中工件的表面温度.
2.2 温度控制方程把工件作为一个半无限大二维问题物体进行处理[5].假设塑性变形的功转化成热量的比例为μ,热传导方程为
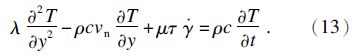
通常情况下若切削速度较高,热传导往往可以忽略,即λ=0.此外,稳态切削时,切削温度对时间的偏导数为零.所以可将式(13)进一步简化为
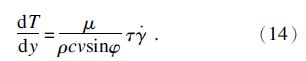

式(14)为工件材料在剪切区的热力控制方程.由式(6)和(12)可知,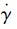 是关于y的函数,而τ是关于y和T的函数.所以可知,式(14)是T关于y的一阶常微分方程.在满足边界条件式(15)的前提下,求解微分方程(14),就可得到剪切区的温度关于切削深度的分布,然后再代入式(12)中,即可得到切削过程中剪切区内剪应力的分布情况.
是关于y的函数,而τ是关于y和T的函数.所以可知,式(14)是T关于y的一阶常微分方程.在满足边界条件式(15)的前提下,求解微分方程(14),就可得到剪切区的温度关于切削深度的分布,然后再代入式(12)中,即可得到切削过程中剪切区内剪应力的分布情况.
剪切力Fs可由主剪切面上的流动应力得到[8]:

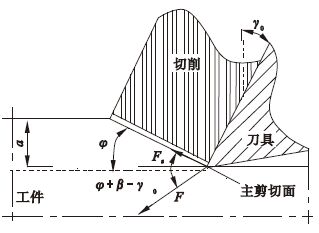
根据图 2所示直角切削的力模型,刀具对工件的切削力为
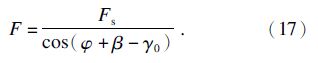
|
图2 直角切削的切削力示意图 Fig. 2 Schematic of orthogonal cutting force |
计算切削力时,涉及到剪切角φ和摩擦角β.本文用Merchant公式计算剪切角:
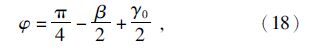


蒙特卡罗模拟(Monte-Carlo simulation)又称统计试验法,是一种利用统计抽样理论近似求解数学问题或物理问题的方法[10].它的主要理论基础是概率论与数理统计中的大数定律与中心极限定理,主要研究手段是通过对每一个随机变量进行大量抽样,并将样本数据代入到分析模型中进行计算,从而获取随机响应的样本值.采用蒙特卡罗模拟方法预测直角切削切削力概率统计特性的具体步骤如图 3所示.首先根据随机参数的概率分布信息独立抽取足够数量的样本,然后将随机参数样本代入到切削力计算模型中,得到切削力样本数据.由此确定直角切削切削力的概率分布特征(如概率分布情况、均值、方差等).

|
图3 基于蒙特卡罗模拟的切削力预测流程图 Fig. 3 Flow chart of the cutting force prediction based on Monte-Carlo simulation |
通过实验可得42CrMo4钢的切削参数为:f0=0.704,p=-0.248,γ0=3°,h=0.025mm,A=612MPa,B=436MPa,C=0.008,n=0.15,m=1.46,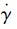 = 0.001s-1, Tm=1800K,Tr= 300K,μ=0.85,ρ= 7800kg/m3,c=500J/(kg · K), Tw=300K,a=0.015mm,b=3mm[7].估算切削速度为v=120m/min时切削力的概率分布特性.
= 0.001s-1, Tm=1800K,Tr= 300K,μ=0.85,ρ= 7800kg/m3,c=500J/(kg · K), Tw=300K,a=0.015mm,b=3mm[7].估算切削速度为v=120m/min时切削力的概率分布特性.
随机参数的方差的取值应通过测试或者实验数据的统计分析获得,如果没有相关数据可以通过以下原则估算.金 属材料的机械性能参数的标准差,可以根据变差系数来确定,一般取0.05[11].随 机变量如果受到大量的独立因素的影响(无主导因素),则它一般服从正态分布[12].
采用确定性方法计算切削力为F=1240N.按照图 3所示步骤,采用105次蒙特卡罗抽样模拟直角切削过程,获取切削力F的样本.采用统计频数直方图的方法获取切削力的概率密度和概率分布图(如图 4和图 5所示).切削力的均值和方差分别为μF=1242N,σF=116.8N.由切削力的均值和标准差可计算获得其变差系数0.094.

|
图4 切削力概率密度函数 Fig. 4 Probability density function of cutting force |

|
图5 切削力概率分布函数 Fig. 5 Probability distribution function of cutting force |
计算结果表明,蒙特卡罗模拟所得切削力的均值与确定性计算的结果基本一致,即模拟所得均值为切削力的无偏估计.切削力具有较强的分散性,切削力的变差系数远大于随机参数的变差系数.切削力正态分布检验图如图 6所示.从图 6可以看出,散点并不聚集在直线上,因此虽然切削参数服从正态分布,计算出来的切削力并不服从正态分布.

|
图6 正态分布检验 Fig. 6 Normal distribution test |
基于蒙特卡罗模拟,提出了一种直角切削切削力的预测与概率统计分析方法.与传统切削力预测方法相比,本文方法 考虑了刀具参数、材料参数、加工工况等随机参数对金属切削过程的影响,更加符合工程实际状况.采用本文方法可以迅速获取金属切削过程中切削力的概率分布特性(均值、方差、概率密度和概率分布等).上述信息对提高工件的加工精度、保证刀具的使用寿命,以及控制切屑的形成等均具有重要指导意义和参考价值.
| [1] | Molinari A,Moufki A.The Merchant’s model of orthogonal cutting revisited:a new insight into the modeling of chip formation[J].International Journal of Mechanical Sciences,2008,50(2):124-131.( 1) 1) |
| [2] | Adibi-Sedeh A H,Madhavan V,Bahr B.Extension of Oxley’s analysis of machining to use different material models[J].Journal of Manufacturing Science and Engineering,2003,125(4):656-666.( 1) 1) |
| [3] | Lalwani D I,Mehta N K,Jain P K.Extension of Oxley’s predictive machining theory for Johnson and Cook flow stress model[J].Journal of Materials Processing Technology,2009,209(12/13):5305-5312.( 1) 1) |
| [4] | 张义民.机械可靠性设计的内涵与递进[J].机械工程学报,2010,46(14):167-188. (Zhang Yi-min.Connotation and development of mechanical reliability-based design[J].Journal of Mechanical Engineering,2010,46(14):167-188.)( 1) 1) |
| [5] | Astakhov V P,Osman M O M,Hayajneh M T.Re-evaluation of the basic mechanics of orthogonal metal cutting:velocity diagram,virtual work equation,and upper bound theorem[J].International Journal of Machine Tools and Manufacturing, 2001,41(3):393-418.( 2) 2) |
| [6] | Tounsi N,Vincenti J,Otho A,et al.From the basics of orthogonal metal cutting toward the identification of the constitutive equation[J].International Journal of Machine Tools and Manufacturing,2002,42(12):1373-1383.( 2) 2) |
| [7] | Li B L,Wang X L,Hu Y J,et al.Analytical prediction of cutting forces in orthogonal cutting using unequal division shear-zone model[J].International Journal of Advanced Manufacturing Technology,2011,54(5/6/7/8):431-443.( 2) 2) |
| [8] | Dudzinski D,Molinari A.A modelling of cutting for viscoplastic materials[J].International Journal of Mechanical Sciences, 1997,39(4):369-389.( 1) 1) |
| [9] | 陈日曜.金属切削原理[M].北京:机械工业出版社,1993. (Chen Ri-yao.Theory of metal cutting[M].Beijing:China Machine Press,1993.)( 1) 1) |
| [10] | Zio E.The Monte Carlo simulation method for system reliability and risk analysis[M].London:Springer,2013.( 1) 1) |
| [11] | Zhang Y M,He X D,Liu Q L,et al.Robust reliability design of banjo flange with arbitrary distribution parameters[J].Journal of Pressure Vessel Technology:Transactions of the ASME,2005,127(4):408-413.( 1) 1) |
| [12] | O’Connor P D T,Kleyner A.Practical reliability engineering[M].5th ed.Chichester:Weily,2012.( 1) 1) |




