实时准确检测磨机负荷是实现磨矿过程优化运行的关键因素之一^[1].基于磨机筒体振动信号开发磨机负荷在线检测仪表已经成为应用干式球磨机、湿式球磨机、半自磨机等不同工艺流程磨矿过程的关注焦点^{[2, 3]}.磨机内部的料球比(MBVR)、磨矿浓度(PD)和充填率(CVR)等磨机负荷参数与磨机负荷直接相关.文献^[4]对不同研磨工况下的实验球磨机筒体振动信号采用传统快速傅里叶变换至频谱获得的单尺度频谱信号进行了对比分析，并建立了基于主元分析( PCA)和最小二乘支持向量机( LS-SVM)的磨机负荷参数软测量模型.针对单尺度频谱存在的高维共线性的特点，文献^[5]通过提取和选择筒体振动信号的多种频谱特征建立了基于组合优化算法的磨机负荷参数软测量模型，但这种基于单尺度筒体振动频谱建立的软测量模型泛化性差、精度低.

筒体振动信号由大量不同强度、不同频率的合力冲击而产生，具有较强的非平稳性.经验模态分解(EMD)可将原始时域信号分解为具有时频特性的内禀模态函数(IMFs)^[6],在故障诊断领域得到了广泛应用^{[7, 8]}.针对这一特点，文献^[9]将筒体振动信号采用经验模态分解(EMD) 自适应分解为具有时频特性的内禀模态函数(IMFs)，结合功率谱密度(PSD)和偏最小二乘(PLS)算法进行了分析；文献^[10]基于PLS模型潜变量方差贡献率选择子模型建立了基于EMD和PLS的选择性集成建模方法；文献^[11]基于互信息(MI)方法分析和选择IMF频谱特征，建立了选择性融合筒体振动和振声频谱特征的软测量模型，对采用IMF频谱特征建模进行了有益尝试，但上述方法的建模精度均不理想.上述基于EMD的文献，只对磨机旋转4个周期的数据进行处理建模，未考虑磨机研磨过程中物料粒度逐渐变小对筒体振动及振声频谱的影响；而且测量模型建模时只是注重于单个尺度IMF频谱的建模精度，未考虑直接融合多尺度IMF频谱，未充分利用PLS算法所固有的能够消除高维输入变量共线性的特性.综上，本文对不同旋转周 期的筒体振动信号进行了EMD分解和分析，并结合工业过程确定筒体振动信号的处理周期，基于已有研究基础，提出基于偏最小二乘的多尺度球磨机筒体振动频谱分析与建模方法，采用实验球磨机的实验数据验证了所提方法的有效性.

1 筒体振动信号自适应分解

采用与文献^[4]相同的实验数据对空转筒体振动信号进行多尺度分析.磨机旋转4周期信号的时域和频域曲线如图 1所示.

图 1(Figure 1)

Fig. 1

图1 磨机空转时筒体振动信号的多尺度曲线 Fig. 1 Multi-scale curves of zero load for shell vibration

图 1分别给出了实验球磨机筒体振动时域和频域的原始和1~13IMF曲线，其中原始频谱的频段的范围是从100~12000Hz，主要原因是前100Hz的频谱是由球磨机简体的自身旋转传动引起的，其幅值远大于后面频谱.图 1表明，EMD可以将磨机空转振动信号按时间尺度从高到低进行自适应分解，尤其是第13个IMF信号，明显为4个周期，与磨机旋转周期相符合；频谱信号的幅值范围为0~0.02Hz，是其他IMF频谱范围的100~1000倍，表明引起磨机筒体振动信号的力主要是由磨机旋转引起的.这是由于实验磨机自身存在的偏心、质心不平衡等因素引起的.可见，不同磨机设备状态不同，其信号分解结果也将存在差异.

从工业实际的角度(如果监测不及时，磨机可在1min内堵磨)和空转信号的稳定程度上(不同旋转周期EMD分析的IMF数量不同)，选择4个分析周期较为适合.本文考虑到磨机研磨过程中物料粒度逐渐变小对筒体振动及振声频谱的影响，对磨机研磨1min内的筒体数据按每段4个旋转周期求取多尺度频谱后，再对全部数据进行平均处理.

借鉴已有文献^[6]中判断IMF频谱贡献的方法，本文定义了IMF频谱相对系数；其定义综合考虑了磨机负荷参数和IMF频谱潜变量贡献率，固定潜在主元数量的IMF频谱模型测误差相对于原始信号频谱模型的建模精度，如式(1)所示:

其中:c_Y^IMFj和c_X^IMFj表示IMF频谱相对于原始信号频谱采用PLS算法提取的第1个潜在变量在Y-Block和X-Block提取的方差贡献率；c_RMSSE^IMF表示IMF信号频谱模型相对于原始信号频谱模型的建模精度；γ₁，γ₂，γ₃表示加权系数，且γ₁+γ₂+γ₃=1.

采用式(1)计算得到不同尺度IMF频谱的相对系数，可以分析不同尺度频谱所蕴含的磨机负荷参数信息的多少，为选择哪些IMF频谱作为磨机负荷参数软测量模型的输入提供量化依据.采用如下公式选择有价值的IMF频谱：

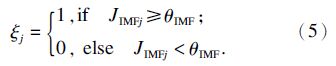
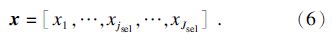
以选择后的频谱 x 为输入，充分利用PLS算法固有消除高维输入变量共线性的特性，建立基于PLS算法的磨机负荷参数软测量模型.

实验在XMQL 420mm×450mm球磨机上进行，该磨机的最大钢球装载量为80kg，设计磨粉能力为10kg/h，转速为57r/min，实验方案和实施方法详见文献^[3].采用与处理球磨机空转数据相同的方法获得建模数据，采用第1节的方法处理IMF频谱，其中PLS模型的潜变量个数统一设为4，γ₁，γ₂和γ₃的取值为0.2，0.2和0.6.对于不同的磨机负荷参数，IMF频谱相对原始频谱的相对系数如表 1所示.

表1

Table 1

表1(Table 1)

表1 IMF频谱相对原始频谱的相对系数 Table 1 The relative coefficient of the IMF spectrum relative to the original spectrum IMF MBVR PD CVR IMF1 0.513 30 -0.140 3 0.469 7 IMF2 0.642 80 -1.764 1 0.283 7 IMF3 0.446 00 -0.481 0 0.234 7 IMF4 0.605 70 -1.309 9 -0.166 8 IMF5 0.088 15 -0.183 6 -0.183 3 IMF6 -0.024 85 -1.298 9 -0.117 8 IMF7 -0.102 90 -1.003 2 -0.672 9 IMF8 0.491 30 -1.538 8 0.097 2 IMF9 0.974 30 -0.759 1 0.445 0 IMF10 0.353 00 -3.960 8 -0.133 4

表1 IMF频谱相对原始频谱的相对系数 Table 1 The relative coefficient of the IMF spectrum relative to the original spectrum

由表 1可知，采用本文准则，不同的IMF频谱相对于原始信号的重要程度不同，并且对于不同的磨机负荷参数各IMF频谱相关系数差别也较大，表明不同尺度频谱蕴含信息不同.针对不同磨机参数，设定不同阈值进行多尺度频谱的选择，根据频谱选择的结果建立PLS模型.本文方法(PSD-IMF-Sel)同时与之前文献中采用的单尺度频谱(PSD-Old)、本文方法处理的单尺度频谱(PSD-Ori)、串行组合全部多尺度频谱(PSD-IMF-All)进行了对比.本文以充填率(CVR)的软测量为例，预测精度和相应建模参数如表 2所示，对比曲线见图 2.

表2

Table 2

表2(Table 2)

表2 磨机负荷参数软测量模型的建模统计结果 Table 2 Soft sensing models’statistical results of the mill load parameters 建模方法 IMF选择阈值 预测误差 选择的IMF频谱 PSD-Old - 0.2306 - PSD-Ori - 0.2340 - PSD-IMF-All - 0.1737 {1~10} PSD-IMF-Sel Thresh_value=0 0.2109 {1,2,3,4,5,6,7,8,9} Thresh_value=0.35 0.2385 {1,2,3,6,8 ,9} Thresh_value=0.4 0.1695 {1,9} Thresh_value=0.45 0.2233 {1}

表2 磨机负荷参数软测量模型的建模统计结果 Table 2 Soft sensing models’statistical results of the mill load parameters

图 2(Figure 2)

Fig. 2

图2 充填率(CVR)软测量模型测试曲线 Fig. 2 Test curves of CVR soft sensing model

表 2和图 2表明，CVR模型选择的IMF频谱为第1个和第9个；建模精度表明本文所提方法是有效的.不同IMF的物理含义需要结合球磨机的有限元仿真和研磨实验深入进行.

本文提出了基于偏最小二乘算法的多尺度球磨机筒体振动频谱分析与建模方法.该方法基于经验模态分解和傅里叶变换获得多尺度频谱，采用基于偏最小二乘算法进行了较为深入分析；定义了不同尺度频谱相对原始频谱的相对系数，基于该系数选择蕴含信息较丰富的多尺度频谱建立磨机负荷参数软测量模型；并采用实验球磨机的实验数据仿真验证了所提方法的有效性.下一步将研究更为有效的多尺度频谱特征的选择和提取方法，并建立更加有效的非线性模型.