2. 沈阳工程学院 自动化学院, 辽宁 沈阳 110136
2.School of Automation, Shenyang Institute of Engineering, Shenyang 110136, China.
Corresponding author: YU Zi-song, E-mail: yzsong1983@163.com
PMSM在低速轻载运行时所需电压较小,因此SVPWM-VSI的非线性增益将使电机电流产生畸变、发热量增大等.造成这种非线性增益的原因主要有[1, 2]:1)开关管的寄生电容效应;2)为了防止上下桥臂开关管与直流母线电压直通所嵌入的死区时间(2~4μs).因此,对VSI非线性增益进行补偿,使其输出平均电压与参考电压指令成线性比例关系是必要的.
根据电压-时间原理,文献[3]利用电流重构判断电流极性,再结合查表的方法对IGBT寄生电容效应进行离线辨识,实现了PWM-VSI非线性增益的准确补偿,但该方法需要前期大量的实验工作,效率较低.文献[4]引入预测电流的方法对电流极性进行判断,同时根据MIT规则抑制模型参数变化,但该方法不能保证补偿器稳定性.
通过将VSI非线性增益视为等效扰动,对平均扰动电压进行补偿的方法可避免因电流极性误判所导致的误补偿[5, 6, 7, 8].文献[5, 6]提出了一种基于q轴扰动电压观测器的方法,实现简单,在中低频下补偿效果较好,但作者并没有对扰动观测器的参数鲁棒性进行评价.文献[7]基于参数变化不产生6n次谐波的思想,引入参数自适应辨识方法将扰动电压分离,但该方法在低频下动态响应较慢.文献[8]引入重复控制对6n次谐波电流进行补偿,同时通过离线测试补偿IGBT的寄生电容效应,实现了样机在1Hz下电流畸变率降到3 % 左右;但电机在低频运行时,该算法需要存储一个周期的电流数据,占用系统大量内存资源.
本文分析了VSI非线性增益的原因,利用矢量旋转的观点解释了零电流钳位现象,提出了一种无需电流极性检测且具有较强参数鲁棒性的VSI非线性电压补偿策略.
1 VSI输出电压非线性分析 1.1 VSI死区效应分析如图 1a所示,为防止同一桥臂上下开关管与母线电压直通所嵌入的一段时间叫做VSI死区时间,记为Tdt.在Tdt内相电流通过经续流二极管与母线连通.

|
图1 单位采样周期内A相桥臂驱动信号与IGBT输出电压 Fig. 1 Drive signal and IGBT output voltage of A leg within one sample period (a)—驱动信号; (b)—输出电压. |
在死区时间内逆变器输出电压为[6]
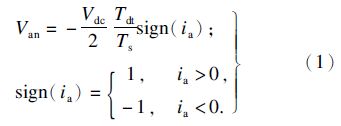
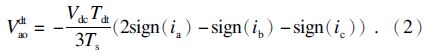
设id,iq分别为旋转坐标系下d,q轴电流, id=0A,Vdc=537V,Ts=100μs,同步转速1Hz,如图 2所示,uddt,uqdt分别为d,q轴死区电压.

|
图2 同步参考坐标系下死区电压 Fig. 2 Dead-time voltage in the synchronous reference frame |
由图 2可知,稳态下q轴死区电压为6n次同步转速附加一直流分量的脉动波,而d轴死区电压为6n次同步转速的脉动波.
1.2 IGBT寄生电容效应分析IGBT的寄生电容效应使VSI输出电压存在动态特性而不是理想状态下的方波[1, 2].文献[1]通过大量实验证明对于特定IGBT其导通时间基本恒定,但关断时间随电流及管子温度而变化,即导通和关闭都存在一定的延时.当电压指令信号足够小时,IGBT的寄生电容效应将使电机相电压发生畸变.
假设ia在IGBT每个关闭时间内近似为常值.根据电压-时间平均原理,如图 1b所示,在IGBT关闭延时时间内VSI 相输出电压为
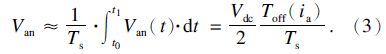
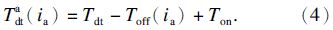
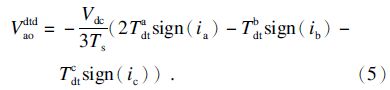
由式(5)可知,IGBT寄生电容效应使每相死区时间随电流瞬时值变化,这将恶化死区补偿的效果,在低速轻载时IGBT寄生电容效应对电流畸变作用更明显.
1.3 VSI零电流钳位效应分析两相静止坐标系下表面式PMSM模型为
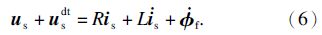
在Ts时间内式(6)可近似表示为
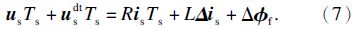
记:xy坐标系为电流矢量坐标系,x,y轴分别为电流矢量 i s的切向与法向.在xy内对式(7)进行分解可得
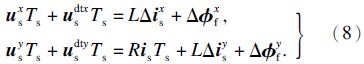
规定:当Δ i sx >0时, i s逆时针旋转;当 Δ i sx <0时,i s 顺时针旋转.
为简单起见,忽略IGBT寄生电容效应,如图 3所示,A,B,C为三相电流矢量轴,i s逆时针旋转,i s0为基波电流矢量,记ang( i s0)为 i s0的相角,ang(MO)为150°.当ang ( i s0)足够接近150°且小于150°时,由于谐波电流的存在使瞬时电流矢量 i s反复穿越图中MO,根据式(2)可知,当ang( i s)>150°时,VSI死区扰动电压为 V 1,由式(8)可得
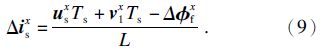
由式(9)知,当 (u sx Ts+ v 1x Ts-Δ φ fx) <0时 i s 顺时针旋转.由图可知,此时 v 1x T <0,因此,当 u sx与-Δ φ fx 对 i s 的逆时针旋转作用较小时,V1将使i s 顺时针旋转.同理,当ang( i s) <150°且ang( i s0) 足够接近150°且大于150°时,VSI死区扰动电压 V6将使i s逆时针旋转.这样,在一段时间内 i s将在150°附近反复运动,即发生零电流钳位现象.

|
图3 C相电流过零附近电压和电流矢量 Fig. 3 Voltage and current vector of the motor when C phase current near zero |
偿策略PMSM同步参考坐标系模型为
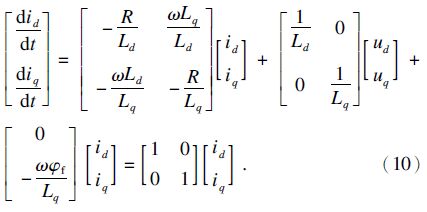
设
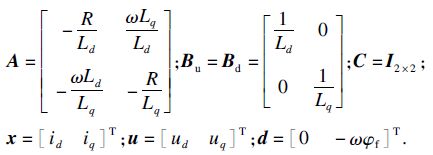
其中,I 2×2为2阶单位矩阵,则式(10)可表示为
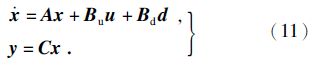
建立同步参考坐标系下扩展PMSM模型:
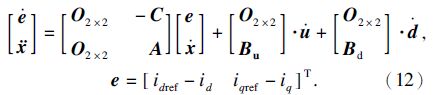
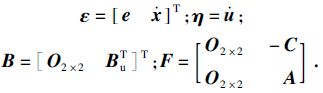
其中,O2×2 为2阶零元素矩阵,可得

可验证 {F,B} 为可控对,设计状态反馈且 η=K · ε=[K2×2e K $\dot x$2×2] · ε ,使得扩展系统渐近稳定.将状态反馈阵展开得
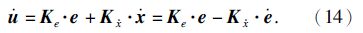
由式(14)可知,当 K2×2e,K $\dot x$2×2对角阵且状态反馈矩阵[K2×2e K $\dot x$2×2]使系统渐近稳定,状态反馈控制器 η= [K2×2e K $\dot x$2×2] ε 等价于电流环的PI调节器.
由文献[9]可知,设计偏差分离双线性控制器: η=η0+η s, η0=Kε. 可得
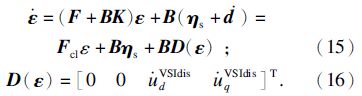
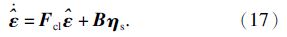
将式(15),式(17)作差可得:
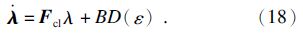
选择[9]:
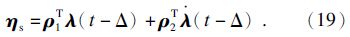
其中: ρ 1T= B1+Fcl;ρ 1T= -B+,B+为B的伪逆; Δ=Ts可保证系统渐近稳定.
由式(18)可得同步参考坐标系下d,q轴补偿电压为
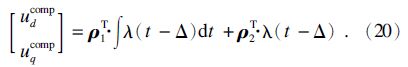
由式(20)可知,扰动电压补偿器包含系统状态的微分,可通过选择适当带宽的低通滤波器对电流滤波,以防止微分放大传感器噪声,增强系统的稳定性.具有SVPWM-VSI 非线性电压增益补偿的系统框图如图 4所示.

|
图4 带SVPWM-VSI非线性补偿的PMSM电流环 Fig. 4 Current loop of PMSM drives system with VSI nonlinear compensator |
利用Matlab/Simulink搭建PMSM矢量控制系统,对VSI非线性补偿策略进行仿真验证.PMSM参数如表 1所示.无VSI非线性补偿时,驱动电机在1Hz空载运行,由图 5可见,相电流出现了明显的畸变,并伴有较强的零电流钳位现象.应用本文所提VSI非线性补偿策略,驱动电机在相同状态下运行,相电流与VSI输入电压指令如图 6,图 7所示.由图 6可见零电流钳位现象已基本消除,电流波形正弦型较好;图 7表明,该补偿器具有较快的动态效应,因此能够补偿电流过零时VSI的阶跃电压扰动.
|
|
表1 永磁同步电动机参数 Table 1 PMSM parameters |

|
图5 电机相电流(无补偿) Fig. 5 Phase current of the motor (without compensation) |

|
图6 电机相电流(有补偿) Fig. 6 Phase current of the motor (with compensation) |

|
图7 电压指令(有补偿) Fig. 7 Input voltage of VSI (with compensation) |
取电机电阻、电感、磁链值分别为1.5Rs,1.5Ls,1.5φf,PI参考模型参数为标称值,电机在1Hz空载运行时相电流及电压指令如图 8,图 9所示.根据图 8可见在参数不确定情况下该补偿策略仍能有效补偿VSI非线性扰动电压,因此,该VSI非线性补偿器具有很好的参数鲁棒性.上述三种情况下的电流畸变率比较如表 2所示.

|
图8 相电流(参数不确定-有补偿) Fig. 8 Phase current(parameter uncertain-with compensation) |

|
图9 VSI输入电压指令(参数不确定-有补偿) Fig. 9 nput voltage of VSI(parameter uncertain-with compensation) |
|
|
表2 相电流THD比较 Table 2 Comparison of phase current THD |
1) 本文所提方法能够准确补偿PMSM矢量控制系统中VSI非线性增益,使三相电流中5次、7次谐波电流含量大大降低,进而减小了电机输出转矩脉动,降低了电机发热量.
2) 通过建立PMSM控制系统的扩展PI参考模型,设计了VSI非线性补偿器.由于该补偿器本质上是利用电流微分量对扰动电压进行观测,因此,该补偿策略具有较快的动态响应特性.在通过适当配置的电流PI控制器参数可基本消除零电流钳位现象.
3) 通过在补偿器输入端加一适当带宽的低通滤波器可消除因电流传感器噪声所导致的补偿器输出发散现象,增强了补偿器的稳定性.
4) 在1.5倍标称电机参数下设计VSI非线性补偿器.仿真表明,该补偿策略能够有效抑制电机参数变化,具有较强的参数鲁棒性.
| [1] | Russel J K,Leggate D,David W S, et al.Effects of parasitics on the control of voltage source inverters[J].IEEE Transactions on Power Electronics,2003,18(1) :140-150.( 2) 2) |
| [2] | Urasaki N,Sebjyu T,Kinjo T,et al.Dead-time compensation strategy for permanent magnet synchronous motor drive taking zero current clamp and parasitic capacitance effects into account[J].IEE Proceeding Electric Power Applications,2005,152(4):845-853.( 2) 2) |
| [3] | Munoz A R, Lipo T A.On-line dead-time compensation technique for open-loop PWM-VSI drives[J].IEEE Transactions on Power Electronics,1999,14(4):683-689.( 1) 1) |
| [4] | Herrn M A,Fischer J R,Gozalez S A,et al.Adaptive dead-time compensation for grid-connected PWM inverters of single-stage PV system[J].IEEE Transactions on Power Electronics, 2013, 28(6):2816-2825.( 1) 1) |
| [5] | Kim S Y,Rho M S,Park S Y.Effective dead-time compensation using a simple vectorial disturbance estimator in PMSM drives[J].IEEE Transactions on Industrial Electronics,2010,57(5):1609-1614.( 1) 1) |
| [6] | 周华伟, 温旭辉, 赵峰, 等.一种新颖的电压源逆变器自适应死去补偿策略[J].中国电机工程学报,2011,31(24):26-32. (Zhou Hua-wei,Wen Xu-hui,Zhao Feng,et al.A novel adaptive dead-time compensation strategy for VSI[J].Proceedings of the CSEE,2011,31(24):26-32.)( 2) 2) |
| [7] | Park D M,Kim K H.Parameter independent online compensation scheme for dead time and inverter nonlinearity in IPMSM drive through waveform analysis[J].IEEE Transactions on Industrial Electronics,2014,61(2):701-707.( 2) 2) |
| [8] | Silverio B,Luca P,Mauro Z.Repetitive-control-base self commissioning procedure for inverter nonidealities compensation[J].IEEE Transactions on Industry Application,2008,44(5):1587-1596. ( 2) 2) |
| [9] | 杨玲玲, 章云, 陈贞丰.不确定非线性系统基于偏差分离的双线性控制[J].自动化学报,2010,36(10):1432-1442. (Yang Ling-ling,Zhang Yun,Chen Zhen-feng.Bilinear control based on model bias separation for uncertain nonlinear systems[J].Acta Automatica Sinica,2010,36(10):1432-1442.)( 2) 2) |




