Corresponding author: LI Guo-jia, E-mail: guojia_li@163.com
多级库存网络是供应链中库存管理的主要形式[1, 2].由于多级库存间的强关联,安全库存可以分布在不同级的仓库中,同级库存也可以相互支援,因此多级库存系统可以比单个库存效率更高[3, 4].为了提高供应链多级存储系统的服务水平、降低库存,多级库存控制策略的研究近年来一直是学术界备受关注的课题[5].
由于顾客到达的随机性、运输车辆行驶时间的随机性、市场价格变化的波动性、存储系统中各种异常事件的突发性等随机因素使供应链存在着大量的不确定性和动态性因素,而供应链库存又与供应链的不确定性和动态性关系密切.目前供应链多级库存控制策略优化模型局限于二级案例,对于网状库存系统的控制策略仅有订货点法 (s,nQ)、报童模型,以及基于控制策略的仿真.基于需求预测和工序提前期对各节点任务作通盘考虑的Push控制策略虽然具有良好的计划性和组织性,但难以适应需求波动频繁的市场环境,而在多阶段生产存储系统中采用看板系统的Pull控制方式时,工人必须“看到”空的看板,才能触发加工作业[6].这就使得看板系统难以运用到广域分布的供应链存储控制中.2000年后,有人开始将Pull控制模式从单工厂推广到供应链的多级库存中[7, 8].但是,由于供应链中不能在多个企业间采用“看板”系统,所谓的“Pull”其实只是“订单拉动”或者“合同拉动”[9, 10],并不能真正发挥“看板系统”降低库存的效率[11].
RFID以其能够对库存项目和运输的途中量进行精确计量和定位,从而能够大大降低多级库存系统的不确定性,为多级库存网络的性能改善提供了一条有效的途径[12, 13].为对供应链多级库存控制策略加以改进,本文基于RFID技术,借鉴单工厂多阶段生产存储系统的Push/Pull策略,以供应链分销网络三级库存系统为例,在不同阶段分别采用Push或者Pull方式作为库存控制策略,设计了8种RFID使能的Push/Pull混合控制策略;为得到各策略更优性能,采用基于仿真的PSO(particle swarm optimization,粒子群优化算法,简称PSO)方法对各策略参数进行了优化,验证了基于仿真的PSO方法对RFID使能的Push/Pull混合控制策略的可行性和有效性,优化后各策略的仿真结果表明8种混合策略中制造商阶段采用Push控制、分销商和零售商阶段采用Pull控制的策略性能最优.
1 RFID使能的Push/Pull混合控制策略的设计及系统假设 1.1 RFID使能的Push/Pull混合控制策略的设计基于RFID技术开发RFID使能的电子看板系统,实现供应链各节点企业的库存量、途中运输量、定发货量等的远程可视,借鉴单工厂多阶段生产存储系统的Push/Pull策略,在供应链分销网络三级库存系统不同阶段分别采用Push或者Pull方式作为库存控制策略,形成不同的RFID使能的Push/Pull混合控制策略.
RFID使能的电子看板系统的构建分为如下三个步骤:
1) 首先将物品装进具有固定规格的盒子并贴上RFID标签,这就使得通过RFID标签能够很方便快捷地识别它们.
2) 为看板信息设计数据库.看板数据库主要包含两类数据表:一类是用于存储单个看板信息的看板数据表;另一类数据表是用于存储包含最大电子看板数及产生的空看板数的看板数量信息.
3) 采用网络技术建立可视化看板系统.在由阅读器、中间件、库存管理计算机、Web服务器和数据库服务器构成的RFID库存管理系统中,库存和看板信息用于RFID系统中实现看板的可视化.分销网络显示在库存管理计算机中,库存和看板信息显示在数据表中.
在由零售商、分销商和制造商构成的供应链分销网络三级库存系统中,设p(p=1,2,…,P),n(n=1,2,…,N)和m(m=1,2,…,M)分别为零售商、分销商和制造商的标号;t(t=1,2,…,T)为运行天数的标号.dk(t) (k 为p,n或m,以下均同)表示第t天 k的毛需求量;KBk(t)表示Pull策略下t天结束时刻节点k产生的空电子看板数;Pushk(t)表示Push策略下t天结束时刻节点k产生的净需求量;Trk(t)表示第t天结束时节点k的运输的途中量;Ik(t)表示第t天结束时节点k的库存量;系统采用RFID使能的Pull策略时,决策变量为KBmaxk,其表示节点 k的最大电子看板数;系统采用Push策略时,决策变量为Tk,其表示节点k的订货提前期.
节点企业采用RFID使能的Pull策略时,通过RFID使能的电子看板系统即时向上级节点企业发出订货指令(生产指令),订货量(生产量)为该节点企业当前库存量与最大看板数之差,按公式可简写为
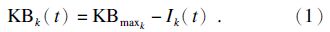
节点企业采用Push策略时,订货量为根据订货提前期预测的毛需求量与在线存储量的差,即毛需求量减去存储量和在途量,按公式可简略地写为
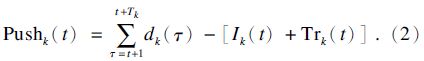
为了便于描述由基于RFID技术的Pull和Push策略组合成RFID使能的Push/Pull混合策略,将供应链分销网络三级库存系统采用的控制方式记为H,Pull控制方式记为0,Push控制方式记为1; 采用三位二进制编码,第一位二进制编码表示制造商阶段各节点企业的库存控制方式,第二位二进制编码表示分销商阶段各节点企业的库存控制方式,第三位二进制编码表示零售商阶段各节点企业的库存控制方式.以H=[000]为例,表示零售商、分销商、制造商阶段均采用Pull控制方式;同理H=[001]表示制造商、分销商采用Pull控制方式,零售商采用Push控制方式;当 H=[010],[011],[100],[101] ,[110],[111]时类似,不再赘述.
1.2 系统假设为不失典型性和代表性假设如下:
1) 制造商生产产品所需时间很短相对于运往分销商的途中运输时间可忽略不计,且原材料供应充足,不同订货(生产)策略造成的生产成本差别可忽略不计;
2) 顾客的产品需求量均为1,各零售商的每天顾客到达数量X服从参数为λ的泊松分布,第t天内顾客到达数量X为g的概率函数为
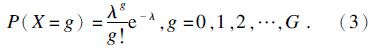
3) 各节点企业均允许缺货,而缺货损失成本只在零售商处计算,即制造商和分销商的缺货不再计算缺货损失成本,当顾客到达的零售商无法满足顾客需求时,顾客将选择放弃购买,发生缺货;
4) 零售商按比例向一个或几个分销商订货,分销商按照比例向一个或几个制造商订货;
5) 系统中节点企业间的运输外包给第三方物流,不同库存控制策略造成的运输成本差别可忽略不计;
6) 系统中各节点企业通过供应链内部网络进行订货,因此订货成本可忽略不计;
7)不同的控制策略对应不同的订货时间和订货量,且各订货策略完整的订货过程均包含订货、发货、运输、到货4个要素.为便于比较,假定订货的各节点企业均在每天结束时刻订货,发货的各节点企业均在每天初始时刻发货,各要素对应的时间点如图 1所示,其中Tnp和Tmn分别为分销商到零售商和制造商到分销商的运输时间.

|
图1 订货过程各要素对应的时间点 Fig. 1 The time of the four elements in the order process |
令hk表示节点k的单位产品存储成本;Vp(t)表示第t天结束时刻零售商p的缺货量;sp表示p的单位缺货损失;CS表示系统总缺货损失;CI表示系统总库存成本;CT表示系统总成本.根据1.2节系统假设,系统的生产成本、运输成本、订购成本与所选订货策略无关,因此采用反映系统服务水平的缺货损失与库存水平的库存成本之和作为目标函数来衡量各策略对供应链多级库存系统的控制性能. 总缺货损失即系统运行一个周期各零售商缺货损失之和:
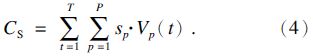
总库存成本即系统运行一个周期零售商、分销商、制造商的库存成本之和:
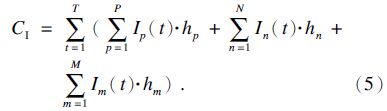
因此,目标函数即系统运行一个周期的总成本:

系统中状态变量为各节点企业每天的库存量,即Ip(t),In(t),Im(t);统计变量为总库存成本CI、总缺货损失成本CS和总运行成本CT.由公式(6)可见,目标函数中的变量均是RFID使能的Push/Pull混合控制策略下决策变量的函数,但供应链中的各种随机因素使这些变量具有不确定性,准确表达式难以给出[14].采用解析方法求解时,须对原问题进行假设和简化,而简化后的问题会与实际问题相差较大,对求解结果造成很大误差.因此,为有效求解问题,采用基于仿真的优化方法[15, 16, 17, 18].
2.2 基于仿真的PSO方法仿真方法能够对系统直观描述,评价不同策略,但无法求出系统的最优解或满意解.作为智能优化算法的PSO方法具有实数编码特点,适于处理实优化问题,且对优化连续问题和离散问题均具有良好效果.根据1.1节所述,各混合策略的决策变量均为实数,因此选择PSO作为优化算法.结合仿真方法与PSO方法,形成基于仿真的PSO方法,在仿真环境中通过PSO方法不断改进输出,实现系统性能优化.
将所建系统仿真模型与PSO流程相结合,初始化粒子群,将每个粒子的位置作为控制变量,输入到仿真模型,得到每个粒子当前评价值,分别将每个粒子当前评价值与其历史最优评价值、当前最优位置与全局最优历史位置相比较来更新其当前最优位置和全局历史最优位置,然后更新粒子位置,反复迭代,直到满足终止条件,停止迭代.
3 仿真结果及分析 3.1 系统及仿真模型参数本文在多种结构多组参数的供应链分销网络三级库存系统下,对8种RFID使能的Push/Pull混合控制策略进行了参数优化及仿真实验.限于篇幅,以图 2所示系统为例进行阐述,M1,M2,M3的单位库存成本分别为0.2,0.1和0.5;N1,N2的单位库存成本分别为0.3和0.7;P1,P2,P3的单位库存成本分别为0.5,0.6和0.8,单位缺货 损失成本分别为10,12和9,每天顾客到达数量泊松分布参数分别为30,40和50;制造商到分销商的运输天数为3,分销商到零售商的运输天数为1,各节点企业初始库存均为100,下游企业向上游企业订货系数如表 1所示(注:表中N1M1表示N1向M1的订货关系,其余类同).仿真整个供应链系统运作100天的情况,对8种RFID使能的Push/Pull混合控制策略在上述给定的初始库存、订货系数、途中运输时间的情况下进行基于仿真的优化,探讨8种策略对系统的控制性能.

|
图2 供应链分销网络三级库存仿真实例 Fig. 2 Simulation case for the three-echelon inventory of supply chain |
|
|
表1 下游企业向上游企业的订货系数 Table 1 The order relation from downstream to upstream enterprise |
PSO主要参数有种群大小、学习因子、最大速度、惯性权重等.种群大小K为整型参数,起着平衡避免陷入局优与收敛速度的作用;学习因子C1和C2具有调节粒子自我总结和向群体中优秀个体学习能力的作用[15];最大速度具有平衡对于PSO性能发挥至关重要的探索能力和开发能力的作用;探索能力和开发能力的平衡主要依靠惯性权重来实现,设定最大速度的作用可通过调整惯性权重实现,不同的问题,获得最好优化效果的惯性权重不同.对于本文所研究问题,通过反复试验,种群大小取K=10,学习因子取C1=C2=1.8,固定惯性权重取ω=0时优化效果较好.系统中有3个制造商、2个分销商和3个零售商,故RFID使能的Push/Pull混合策略的决策变量共有8个,因此粒子维数为D=8;PSO迭代终止条件取迭代次数J=100.
3.3 实验结果如2.1节所述,仿真系统中评价各策略性能的主要指标为供应链运行总成本,故PSO方法在迭代求解过程中,每个粒子的评价值为仿真系统运行一个周期的总成本,8种策略迭代100次对应的总成本随迭代次数的变化曲线如图 3所示,再将优化后的各策略参数作为控制变量输入到仿真模型进行仿真.由于每次仿真实验中,随机变量都可能存在一定的误差,因此仿真100次,得到平均意义下的总成本,以避免每次实验中随机变量可能存在的误差对仿真结果准确性造成的影响,各策略仿真的平均总成本对比如图 4所示.

|
图3 各策略总成本随迭代次数的变化曲线 Fig. 3 The graphs between total cost and iterations |

|
图4 各策略仿真平均总成本对比图 Fig. 4 The graphs of total average cost of the strategies |
1) 从图 3可见,基于仿真的PSO方法在有限的迭代次数内可以对各RFID使能的Push/Pull混合策略进行有效优化,验证了基于仿真的PSO方法对优化RFID使能的Push/Pull混合策略的可行性和有效性;
2) 从图 4可见,各混合策略中制造商阶段采用Push策略,分销商和零售商采用Pull策略的控制性能最优.
对上述结果进一步分析可得:
本文求解问题的决策变量均为实数,使得PSO算法实数编码的优点得以充分发挥,故在各混合策略的优化中均表现出良好的效果.
作为供应链中核心企业的制造商处于最上游,远离客户需求所在的市场端,是供应链分销网络物流的源头,采用根据一定时期的预测需求量下达生产指令的Push控制,可以使其库存量及产量安排兼顾下游节点企业,能够有效保证生产具有良好的计划性、组织性以及物流的平稳性;处于中下游的分销商和零售商在供应链分销网络中接近于客户需求所在的市场端,处于中转地位具有物流分流作用,采用根据局部存储信息由远程可视化看板来下达订货指令的RFID使能的Pull控制,可以使每个处于中下游的各节点企业具有高度自治性,能够及时主动地满足局部需求,对市场需求响应快速合理.
需要指出的是,3.1节提到的在多种结构多组参数的供应链分销网络三级库存系统下,对8种RFID使能的Push/Pull混合控制策略进行的参数优化及仿真实验,与上述结论一致.
4 结 论RFID技术的产生为供应链多级库存性能的改善提供了新方法.本文基于RFID技术借鉴单工厂多阶段的Push/Pull策略,以供应链分销网络三级库存系统为例设计了8种RFID使能的Push/Pull混合控制策略;并采用基于仿真的PSO方法对各策略参数进行了优化,验证并分析了基于仿真的PSO方法对优化RFID使能的Push/Pull混合策略的可行性和有效性;优化后各混合策略的仿真结果表明制造商阶段采用Push控制、分销商和零售商阶段采用Pull控制策略的性能最优,为供应链多级库存管理实践提供了有益参考.
| [1] | Moinzadeh K.A multi-echelon inventory system with information exchange[J].Management Science,2002,48(3):414-426.( 1) 1) |
| [2] | 赵晓煜,汪定伟.供应链中二级分销网络的设计优化模型[J].管理科学学报,2001,4(4):22-26. (Zhao Xiao-yu,Wang Ding-wei.The design and optimization model of secondary distribution network in supply chain[J].Journal of Management Science in China,2001,4(4):22-26.)( 1) 1) |
| [3] | Kiesmüller G P,de Kok T G ,Smits S R,et al.Evaluation of divergent N-echelon (s,nQ)-policies under compound renewal demand[J].OR Spectrum,2004,26(4):547-577.( 1) 1) |
| [4] | Schneider H.Effect of service levels on order-points and order-levels in inventory models[J].International Journal of Production Research,1981,19(6):615-631.( 1) 1) |
| [5] | Lagodimos A G,Koukoumialos S.Service performance of two-echelon supply chains under linear rationing[J].International Journal of Production Economics,2008,112(2):869-884.( 1) 1) |
| [6] | Wang D W,Xu C G.Hybrid Push/Pull control strategy simulation and its applications[J].Production Planning and Control,1997,8(2):142-151.( 1) 1) |
| [7] | Lee Y H.Supply chain model for the semiconductor industry of global market[J].Journal of Systems Integration,2000,10(3):189-206.( 1) 1) |
| [8] | Ahn H S,Kaminsky P.Production and distribution policy in a two-stage stochastic push-pull supply chain[J].IIE Transactions,2005,37(7):609-621.( 1) 1) |
| [9] | Cachon G P.The allocation of inventory risk in a supply chain:push, pull,and advance-purchase discount contracts[J].Management Science,2004,50(2):222-238.( 1) 1) |
| [10] | Cochran J K,Ha K.Optimal design of a hybrid push/pull serial manufacturing system with multiple part types[J].International Journal of Production Research,2008,46(4):949-965.( 1) 1) |
| [11] | 贺成志,马浩军,彭训贵.推拉集成式生产管理模式在MES中的应用[J].计算机应用,2006 (sup2):330-332. (He Cheng-zhi,Ma Hao-jun,Peng Xun-gui.The model of push-pull integrated production management model in the application of MES[J].Computer Applications,2006 (sup2):330-332.)( 1) 1) |
| [12] | Ballestinb F,PEREZa á.Static and dynamic policies with RFID for the scheduling of retrieval and storage warehouse operations[J].Computers & Industrial Engineering,2013,66(49):696-709.( 1) 1) |
| [13] | 尹作重,杜峻,李晨希, 等.RFID在供应链信息集成中的应用[J].制造自动化,2013,35(4):14-16. (Yin Zuo-zhong,Dun Jun,Li Chen-xi,et al.RFID in the supply chain information integration[J].Manufacturing Automation,2013,35(4):14-16.)( 1) 1) |
| [14] | 李怡娜,叶飞,徐学军.可控提前期供应链库存优化的费用分担模型[J].系统工程学报,2009,24(1):9-17. (Li Yi-na,Ye Fei,Xu Xue-jun.Cost allocation model for optimizing supply chain inventory with controllable lead time[J].Journal of Systems Engineering,2009,24(1):9-17.)( 1) 1) |
| [15] | 高镜媚,汪定伟.三级网状随机性库存控制策略的仿真优化[J].控制理论与应用,2009,26(11):1218-1224. (Gao Jing-mei,Wang Ding-wei.Simulation-based optimization on three-echelon network stochastic inventory control policies[J].Control Theory & Applications, 2009,26(11):1218-1224.)( 2) 2) |
| [16] | 李永先,胡祥培,熊英.物流系统仿真研究综述[J].系统仿真学报,2007,19(7):1412-1416. (Li Yong-xian,Hu Xiang-pei,Xiong Ying.Overview on logistics system simulation[J].Journal of System Simulation,2007,19(7):1412-1416.)( 1) 1) |
| [17] | 田俊峰,杨梅.随机需求条件下生产-库存系统优化与仿真[J].系统仿真学报,2004,16(11):2522-2524. (Tian Jun-feng,Yang Mei.Optimization and simulation of production-inventory system with stochastic demand[J].Journal of System Simulation,2004,16(11):2522-2524.)( 1) 1) |
| [18] | 李新,王宛山,韩洋,等.一种柔性供应链仿真系统的研究与实现[J].系统仿真学报,2013,25(6):1270-1278. (Li Xin,Wang Wan-shan,Han Yang,et al.Novel flexible supply chain simulation system[J].Journal of System Simulation,2013,25(6):1270-1278.)( 1) 1) |




