无黏性土渗透破坏是常见的工程问题^{[1, 2, 3]}，而临界水力梯度的计算与分析对工程安全及防护研究具有重要意义.现阶段，对无黏性土临界水力梯度的计算大多依靠以太沙基理论^[4]为基础的经验公式.但是这些经验公式常常过于简化，忽略的因素也较多，对于复杂地质条件下的工况很难进行更准确的计算，因而渐渐不能满足日益提高的工程要求.

PFC^3D(particle flow code in 3 dimension)即三维颗粒流程序，是ITASCA公司基于颗粒离散单元方法开发的用来模拟圆形颗粒介质运动及其相互作用的大型三维数值程序.该程序不但可以表示宏观物质的物理特性，而且可以反映其他方法无法实现的微观特性.国内外学者们已应用该程序在相关领域进行了较多的数值模拟研究，并取得了一定的成果^{[5, 6, 7, 8]}.但是在PFC^3D中，与渗流耦合的细观数值模拟的应用却较少.本文采用颗粒流离散元法理论模拟饱和多孔介质中颗粒的力学行为，采用CFD计算技术模拟孔隙流体的运动.应用这种方法^[9]，不仅可以得到实验室很难观测到的颗粒的运动和应力分布等这些细观参量，同时还可以对流体速度、流线以及压力分布等进行分析，通过将两者结合实现对渗透破坏问题的分析研究.本文应用上述的颗粒-渗流模型，首先对渗流实验算例进行了计算，从而验证计算的正确性和有效性.再对不同颗粒摩擦系数下无黏性土渗流临界水力梯度进行数值计算.最后，将模拟结果与应用经验公式计算得到的结果进行对比研究与分析.

该模型的主要原理在于求解不可压缩流体的连续方程和N-S方程时，考虑流体单元中土颗粒的影响，得到每个流体单元的压力、速度矢量和孔隙率等参数.再将流体流动所产生的渗透力以体积力的形式作用于流体单元中的土颗粒上，并将同样大小的力耦合到流体方程内^[9].

图 1为一个体积ΔV=ΔxΔyΔz的流体控制体单元，在该流域中含有n_p个球体单元.通过对图 1中控制体进行受力分析可得到单个土颗粒受到作用力的一般表达式为

图 1(Figure 1)

Fig. 1

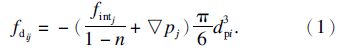
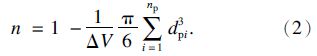
图1 流体控制体单元示意图 Fig. 1 The sketch of the fluid control volume

对于流固两相介质中的不可压缩流体，其密度为常数，连续方程和N-S方程分别如下：

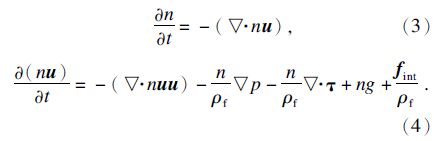
假设颗粒流体之间的相互作用力只来自于压力梯度∇p_j，则

对于压力梯度的计算可采用如下方程：

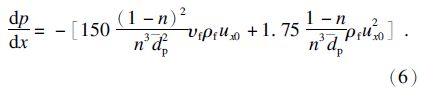
由于式(6)中的u_x0是渗透的平均流速，而实际流速应为u_x=u_x0/n.并且土颗粒受到的渗透力实际上是由水流与颗粒之间的相对流速产生的，故需将式(6)中绝对速度替换为相对速度，u_rx=v_x－u_x (v_x为土颗粒的平均速度).所以得到压力梯度的一般形式为^[9]

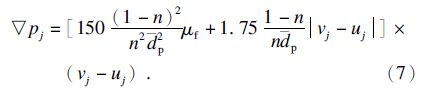
中国地质大学黄琨做了等径球粒立方体排列孔隙介质渗流实验^[10],该实验采用有机玻璃板作为模型管壁.此材料不仅是透明的，便于观察实验现象，而且具有一定的强度，管壁可以在实验过程中承受较高的水压.填充小球为高精度亚克力球，粒径为10mm，横截面填充小球数为2×2，见图 2，并按照立方体排列的方式填充至有机玻璃管内.

图 2(Figure 2)

Fig. 2

图2 横截面填充小球示意图 Fig. 2 he sketch of the small ball in cross-section

整个等径球粒立方体排列孔隙介质模型长3m，考虑到实验管两端的“入口效应”和“出口效应”，进出口段的测压孔分别设置在距离进口端和出口端 25cm的位置，以保证测量的水压能反映孔隙介质的水头损失规律，如图 3所示^[10].

图 3(Figure 3)

Fig. 3

图3 渗流实验装置示意图 Fig. 3 The sketch of seepage flow experiment equipment

实验中通过调节进水阀门来控制进口流量，待2根测压管的测压水头值稳定后，使用量筒加秒表测出流量大小^[10].

按照实验模型尺寸，选用PFC^3D中的墙单元作为模型的管壁，选用球单元来模拟实验中的小球，数值模拟基本参数见表 1.

表1

Table 1

表1(Table 1)

表1 数值模拟基本参数 Table 1 Parameters of materials in numerical simulation 颗粒模型尺寸/m 3×0.02×0.02 球体粒径/mm 10 摩擦系数 0.6 球体密度/(kg · m-3) 2500 接触(切向和法向)刚度/MPa 100,100 流体 密度/(kg · m-3) 1000 黏性系数/(Pa · s) 0.001

表1 数值模拟基本参数 Table 1 Parameters of materials in numerical simulation

通过程序自带的FISH语言，按照立方体排列的方式生成球单元，生成后的模型见图 4.

图 4(Figure 4)

Fig. 4

图4 PFC3D颗粒模型图 Fig. 4 PFC3D particle model

计算时，生成240个(60×2×2)尺寸为50mm×10mm×10mm的流体域，在x=0m和x=3m处设置不同的流速边界，并监测x=0.25m与x=2.75m之间的压强差，待稳定后记录数据，将其换算成水力梯度，与实验结果进行对比，如图 5所示.

图 5(Figure 5)

Fig. 5

图5 模拟结果与实验结果对比图 Fig. 5 Comparison between simulation results and experiment results

由图 5可知，计算结果与实验结果仍存在着一定的差异，一方面可能是由于实验中边界对结果产生的影响在计算中没有有效地体现出来；另一方面，模型中使用的理想化公式可能与实际情况也存在着一定的差异.但总体上，模拟结果与实验结果基本吻合，从而验证了该模型对渗流计算的有效性.

在PFC^3D中，影响黏聚力的因素主要为颗粒间的连接强度，影响摩擦角的因素主要为颗粒间的摩擦系数^[5].所以建模时，用设置颗粒间的连接强度为0的方法来实现对土体无黏性的模拟，而颗粒摩擦系数则采用如下9组参数来进行计算模拟，分别为0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8.其他参数设置见表 2.

表2

Table 2

表2(Table 2)

表2 PFC3D模拟细观参数 Table 2 Microscopic parameters of PFC3D 颗粒模型尺寸/m 0.24×0.24×0.84 颗粒最小粒径/m 0.006 颗粒最大粒径/m 0.008 球体密度/(kg · m-3) 2650 接触(切向和法向)刚度/MPa 100,100 孔隙率 0.45 流体 密度/(kg · m-3) 1000 黏性系数/(Pa · s) 0.001

表2 PFC3D模拟细观参数 Table 2 Microscopic parameters of PFC3D

采用如上所示参数，生成模型见图 6.

图 6(Figure 6)

Fig. 6

图6 PFC3D数值模拟试样 Fig. 6 The sketch of PFC3Ddata sample

图 6为生成模型后，在自重作用下的初始稳定图.可以看出，图中颗粒总体有效高度比初始模型设置高度要小.通过计算，稳定后有效高度变为0.753m，而孔隙率则缩小到0.39.

通过赋予上述模型不同摩擦系数参数，并不断调节下底面的压强边界条件，使水流从下向上流过，直至发生破坏，如图 7所示.图 8和图 9中列举了颗粒摩擦系数为0.2时的临界水力梯度计算过程.当压强边界为8.05kPa时，如图 8所示，试件结构完整，未发生破坏，并且流体流量趋于稳定，不随时间变化.而当压强边界为8.1kPa时，如图 9所示，土体结构下方出现明显破坏，并且流量发生明显变化，因而认为颗粒摩擦系数为0.2时的临界水力梯度为8.1kPa.本文采用上述判别方法，得到不同颗粒摩擦系数下的临界水力梯度关系曲线，如图 10所示.

图 7(Figure 7)

Fig. 7

图7 流体域计算示意图 Fig. 7 The sketch of fluid domain

图 8(Figure 8)

Fig. 8

图8 压强边界8.05kPa下颗粒摩擦系数0.2的 Fig. 8 Numerical result with particle friction coefficient of 0.2 under the pressure boundary of 8.05kPa

图 9(Figure 9)

Fig. 9

图9 压强边界8.1kPa下颗粒摩擦系数0.2的计算结果 Fig. 9 Numerical result with particle friction coefficient of 0.2 under the boundary pressure of 8.1kPa

图 10(Figure 10)

Fig. 10

图10 不同颗粒摩擦系数下的临界水力梯度关系曲线 Fig. 10 Critical hydraulic gradient with different particle friction coefficients

在渗流作用下无黏性土临界水力梯度的计算中，常用的公式为太沙基公式^[4]，但该公式在推导中忽略了土 颗粒之间的摩擦力和黏聚力，根据单位体积土体在水中的重量和作用在土体上渗透力的受力平衡，得到临界水力梯度的计算公式：

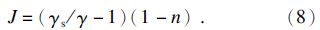
在后续的研究中，考虑了更为复杂的情况，假设单位土体引起的侧压力产生了摩擦力，则得到^[4]：

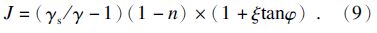
PFC^3D中，在土体无黏性的情况下，颗粒摩擦系数与土体摩擦系数基本一致^{[5, 6]}.采用上述公式进行计算，土的侧压力系数通过PFC^3D求得，将该公式计算得到的结果绘制于图 10中，可见临界水力梯度大小随着颗粒摩擦系数增加而增大.而PFC^3D计算结果与公式计算结果基本一致，如表 3所示，表明PFC^3D对无黏性土的临界水力梯度计算的正确有效性.

表3

Table 3

表3(Table 3)

表3 PFC3D计算结果与经验公式计算结果对比 Table 3 Comparison between the numerical results of PFC3D and empirical formula 颗粒摩擦 系数 PFC3D计算结果 经验公式 计算结果 两组结果 相差百分比 0.0 0.982 1.012 2.96 % 0.1 1.030 1.048 1.71 % 0.2 1.098 1.078 -1.79 % 0.3 1.165 1.103 -5.61 % 0.4 1.193 1.134 -5.17 % 0.5 1.206 1.161 -3.91 % 0.6 1.213 1.188 -2.07 % 0.7 1.220 1.214 -0.43 % 0.8 1.226 1.241 1.21 %

表3 PFC3D计算结果与经验公式计算结果对比 Table 3 Comparison between the numerical results of PFC3D and empirical formula

在实际工程中，工程和地质结构条件均较为复杂，传统公式仅能考虑简单的情况且忽略因素较多，此时则应该采用PFC^3D对复杂条件下无黏性土的临界水力梯度进行计算，从而为工程计算提供可靠的参考和依据.

1) 采用PFC^3D中的渗流模型对已有实验进行数值模拟，模拟结果与实验结果基本一致，说明计算模拟的正确有效性，表明PFC^3D中的渗流模型可以有效用于模拟多孔介质中的渗流问题.

2) 采用PFC^3D对无黏性土的临界水力梯度计算得到的结果与使用经验公式计算得到的结果基本一致，并且无黏性土的临界水力梯度随着颗粒摩擦系数增加而增大.

3) 对复杂条件下的无黏性土临界水力梯度计算，应该采用适用性更强的PFC^3D进行模拟计算.