由于盾构隧道施工技术具有对周边环境影响小、机械化程度高及施工速度快等优点被广泛应用到城市地铁开挖工程.然而盾构隧道的开挖面支护压力大小的设定直接影响到地层移动及地表沉降，尤其穿过地面既有建筑物及地下管线等复杂环境时对开挖面支护压力的要求非常严格.开挖面支护压力过小易导致地表沉降过大，甚至是塌陷；反之，支护压力过大则导致地表隆起破坏^{[1, 2]}.目前，泥水平衡盾构和土压平衡盾构开挖面均采用预先设定泥水或土压支护压力以保证开挖面稳定性.

隧道开挖面的最小支护压力往往受到多重因素的影响，如覆跨比、土体重度、内摩擦角、黏聚力、地下水位等.目前国内外很多学者运用极限平衡分析、极限分析和模型试验针对开挖面极限支护压力作了大量研究.Leca等^[3]采用极限分析法研究了圆形隧道开挖面的极限支护压力.Anagnostou等^{[4, 5]}基于筒仓理论通过考虑楔形体和棱柱体极限平衡列出分析体的水平和竖直方向上的平衡方程进行求解，从而获得维持开挖面稳定所需要的最小支 护压力.Atkinson等^[6]运用极限分析法对砂土地层圆形隧道极限支护压力进行研究，并推导出了相应的计算公式.魏纲等^[7]采用三维极限平衡法研究了隧道开挖面极限支护压力.

本文基于极限平衡法及Flac^3D数值模型研究了砂土地层盾构开挖面的失稳模式及极限最小支护压力，并对比分析两种计算结果.揭示了现有极限平衡法理论模型中计算上覆土压力存在的缺陷及预测极限支护压力的误差.

文中基于Flac^3D软件建立了数值计算模型用于研究开挖面极限支护压力，计算模型中设定 侧压力系数值为静止土压力系数K₀=1－sinφ.实际工程中开挖面的支护压力应为梯形荷载，因此文中采用隧道开挖面中心点处的压应力σ_h代表开挖面支护压力大小.

表1

Table 1

表1(Table 1)

表1 数值模拟方案 Table 1 The scheme of numerical simulation 方案编号 覆跨比C/D 内摩擦角 φ/(°) 1 0.5 20 2 0.5 25 3 0.5 30 4 0.5 35 5 0.5 40 6 1.0 20 7 1.0 25 8 1.0 30 9 1.0 35 10 1.0 40 11 2.0 20 12 2.0 25 13 2.0 30 14 2.0 35 15 2.0 40 16 4.0 20 17 4.0 25 18 4.0 30 19 4.0 35 20 4.0 40

表1 数值模拟方案 Table 1 The scheme of numerical simulation

对于开挖面支护压力大小的表示，引入支护压力比的概念^[8]：

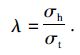
在数值模型中，采用的隧道直径为6m，管片厚度为0.35m.模型具体尺寸如图 1所示，模型中除了地表为自由边界以外，模型四周及底部边界均为法向约束.土体采用摩尔库伦屈服准则，材料参数如表 2所示.数值模拟过程可以分为如下几个步骤：

图 1(Figure 1)

Fig. 1

图1 数值模型示意图(C/D=1.0) Fig. 1 The three dimensional numerical model (C/D=1.0)

表2

Table 2

表2(Table 2)

表2 材料力学参数 Table 2 Mechanical parameters 材料 名称 弹性 模量 E/MPa 泊松 比ν 重度γ/ (kN · m－3) 内摩 擦角 φ/(°) 静止土 压力系数K0 土层 20 0.35 18.5 20~40 1－sinφ 管片 30000 0.25 25 — —

表2 材料力学参数 Table 2 Mechanical parameters

1) 建立三维数值计算模型，设定初始土体静止土压力系数 K₀=1－sinφ，并计算初始地应力.

2) 由于本文研究重点是隧道开挖面的极限最小支护压力，因此进行数值模拟时一次开挖至12m，并设置盾构管片.同时在开挖面施加与原始地层侧向静止土压力值相等的梯形支护压力.

3) 不断减少开挖面的支护压力，并对开挖面中心点的水平位移进行监测.通过开挖面中心点水平位移随着开挖面的支护压力的变化曲线确定极限最小支护压力，即支护压力变化很小而开挖面中心点的水平位移急剧增大时，认为此时的支护压力比即为最小极限支护压力.

不同埋深比下开挖面失稳时的位移云图，见图 2.可以看出砂土地层中盾构开挖面的破坏模式基本与三维楔体模型一致；开挖面前方为楔型状，滑动块顶部为烟囱状.开挖面的破坏发展由开挖面顶部向地表发展，而且随着埋深的增大，砂土的成拱效应有效限制了地层的移动，使得地表最大沉降也显著减少，这说明随着埋深的增加，开挖面的破坏更难以延伸至地表面.该趋势与VERMEER等^[9]的离心模型试验结果相一致.

图 2(Figure 2)

Fig. 2

图2 开挖面失稳时位移云图(C/D=2.0,φ =35°) Fig. 2 Displacement contour of tunnel face

图 3为土层不同内摩擦角下支护应力比与开挖面中心点水平位移的关系曲线(D=6m,C/D= 0.5).秦建设^[8]将开挖面的变形与破坏分为3个阶段：第一阶段中当支护压力比减小时开挖面发生微小的变形；随着支护压力比的不断减小开挖面将发生显著的位移为第二阶段；第三阶段中支护压力减少至极限最小支护压力时开挖面变形将无限增大，数值模型不能收敛.

图 3(Figure 3)

Fig. 3

图3 不同内摩擦角下的极限支护压力(C/D=0.5) Fig. 3 Limit supporting pressure at different friction angles of soil

由图 4可以看出埋深比(C/D)不变的情况下，极限支护压力比λ随着内摩擦角的增大不断减小，当内摩擦角增大至某个值(约35°)时，极限支护压力比的减小不再显著，表明此时已形成“土拱效应”.

图 4(Figure 4)

Fig. 4

图4 内摩擦角对极限支护压力比的影响 Fig. 4 The effect of the friction angle on limit supporting pressure ratio

数值模型计算得到的极限支护压力与内摩擦角的关系曲线见图 5.极限支护压力随着内摩擦角的增大而减小，随着埋深的增大而增大.当土层内摩擦角较小时，埋深(C)对极限支护压力的影响较为显著；内摩擦角为20^o时极限支护压力由C/D=4.0时的最大值59.783kPa逐渐减小至C/D=0.5时的19.706kPa.当土层内摩擦角足够大时，砂土的成拱效应致使破坏面不能延伸至地表，因此埋深比的增大不会引起极限支护压力的增大.图 5表明，土层内摩擦角为40^o时，极限支护压力值随着埋深的变化不明显，表明土层成拱效应起到限制地层移动的作用^{[9, 10, 11]}.

图 5(Figure 5)

Fig. 5

图5 埋深比对极限支护压力的影响 Fig. 5 The effect of buried depth ratio on limit supporting pressure

采用文献^[7]的三维楔体模型分别计算了埋深比(C/D)为0.5，1.0，2.0及4.0三种工况，计算结果见图 6.可以看出内摩擦角较小时随着埋深比的增大，开挖面极限最小支护压力也逐渐增大；但是埋深比大于2.0时极限支护压力数值基本趋于稳定.当埋深比(C/D)=0.5,φ=20°时，极限平衡解为15.21kPa，数值解则为 19.94kPa，相对误差为23.7 % ；埋深比(C/D)增加至4.0时，极限平衡解及数值解分别为19.86，59.783kPa，相对误差达到66.7 % .可见，埋深比越大极限平衡模型计算误差则越大，计算结果偏于不安全，运用该模型预测开挖面最小极限支护压力时应充分意识到这一点.实际上，滑动块体的侧压力系数并非常量，而是随着开挖面的位移而动态变化，这也是极限平衡模型计算结果误差较大的主要原因.

图 6(Figure 6)

Fig. 6

图6 三维梯形楔体模型计算结果 Fig. 6 The computed results of wedge model

1) 随着土层内摩擦角的增大，极限最小支护压力逐渐减小；埋深比的增加使支护压力比λ逐渐减小，但是极限最小支护压力却逐渐增大.由于砂土的成拱效应，极限支护压力值远小于其静止土压力，并且埋深比增大到一定值时开挖面破坏区域不会延伸至地表.

2) 极限平衡模型得到的计算结果主要依赖于侧压力系数K₀的取值；而侧压力系数并非常量，其大小随着滑动块体的位移和土层深度而变化.因此，利用极限平衡模型计算出的极限最小支护压力随着埋深比的增大其误差也逐渐增大；计算结果偏不安全.