全断面岩石掘进机(full face hard rock tunnel boring machine，TBM)是用于开凿岩石隧道的大型高端工程装备，适用于城市地铁、地下及山区隧洞的开挖，具有快速、优质、安全等优点^[1].刀盘系统作为掘进机的核心工作部件，直接与岩石作用，有破岩、稳定掌子面等功能，承受空间多点随机冲击载荷耦合作用，结构振动剧烈，出现刀具异常磨损、刀盘面板开裂及轴承密封失效等故障^{[2, 3]}.因此，要求结构具有强度好、振动小、可靠性及疲劳寿命高等特点，有必要在设计阶段就对TBM刀盘系统的动力学特性进行分析，提出结构参数的设计依据.

国内外学者从20世纪60年代开始就对TBM刀盘系统设计展开了诸多有益的研究.文献^{[4, 5]}对TBM刀盘滚刀载荷进行测试，研究滚刀载荷变化规律，并统计其分布特征.文献^[6] 研究硬岩刀盘系统设计方法，从滚刀布局的角度评价刀盘的承载平衡性能.文献^{[7, 8]}提出基于遗传算法和协同演化算法的滚刀平面布置设计方法，研究在不同掘进模式下多滚刀破岩过程及刀间距设计方法.文献^{[9, 10]}从盾构机能耗性能的角度提出新的刀盘比能计算模型，确定不同工况下滚刀切削深度的最佳范围.文献^{[11, 12]}采用离散元方法研究围岩特性、刀间距等参数对刀盘性能的影响.

综上所述，国内外学者主要采用现场测试、相似模型试验及数值仿真等手段，研究滚刀破岩机理及受力模型、掘进随机载荷及滚刀平面布局等问题，而对强冲击下刀盘系统整体的振动问题研究还没有涉及，目前也尚无TBM刀盘系统固有特性及参数灵敏度分析的文献.因此，本文建立了分体式刀盘系统多自由度耦合动力学模型，基于特征值问题求解系统的固有频率和振型，同时分析了不同模态下固有频率对刀盘结构参数的灵敏度及影响规律，从而为刀盘系统动态性能优化提供设计参考.

在TBM刀盘系统中，电机经过行星齿轮减速器后，将动力通过联轴器传至小齿轮，多个小齿轮同时顺时针驱动大齿圈，大齿圈通过螺栓固定传力环及法兰，进而带动刀盘旋转，系统结构示意图如图 1所示(图中仅画出其中一个电机驱动系统)，刀盘分瓣结构形式如图 2所示.

图 1(Figure 1)

Fig. 1

图1 TBM刀盘系统组成 Fig. 1 Components of TBM cutterhead system

图 2(Figure 2)

Fig. 2

图2 刀盘分瓣结构 Fig. 2 Structure of TBM split-cutterhead

基于集中参数质量法建立TBM分体式刀盘系统多自由度耦合动力学模型，其中弯扭耦合动力学模型如图 3所示，其余自由度模型详见参考文献^[13]，同时动力学微分方程也在该文献中.

图 3(Figure 3)

Fig. 3

图3 TBM刀盘系统弯扭耦合动力学模型 Fig. 3 Bend-torsion coupled dynamic model of TBM cutterhead system

对系统进行振动模态分析，忽略文献^[13]中动力学微分方程的阻尼、间隙及外部激励项，采用平均刚度代替齿轮副时变啮合刚度和轴承时变刚度，得到与之对应的特征值问题为

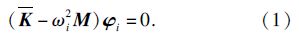
本文基于辽西北供水工程项目硬岩刀盘系统设计参数：刀盘直径为8.53m，驱动功率为3440kW，刀盘额定转速为5.6r/min，其余参数见表 1.

表1

Table 1

表1(Table 1)

表1 刀盘系统基本参数 Table 1 Basis parameters of cutterhead system 系统参数 刀盘分体 刀盘中心块 大齿圈 支撑盾体 小齿轮 驱动电机 质/kg mi=1.74e4 mL=5.91e4 mr=846 md=6.2e4 mp=167 转动惯量/(kg · m2) IL=1.16e6 Ir=1.55e3 Ip=1.98 Im=31.68 kLζi=4.01e9 kkeqx=1e11 等效支撑刚度/(N · m-1) kLηi=1e10 keqy=1e11 keqr=2e10 keqdz=1e12 kLi=2.5e10 keqL=8e10 keqz=3.6e11 keqd=1e12 keqp=2.7e10 等效扭转刚度/(N · m · rad-1) krLQ=6.06e12 kmpQ =4.09e6 平均啮合刚度/(N · m-1) km=5.4e9 齿数 Zr=174 Zp=14 模数/mm m=22 啮合角/(°) α=20°

表1 刀盘系统基本参数 Table 1 Basis parameters of cutterhead system

求解系统的自由振动微分方程组，系统振动共有59个自由度，可以求出59个固有频率和振型，鉴于刀盘实际激振频率情况^{[4, 5]}，本文列出刀盘系统的前15阶振型和固有频率，如表 2所示.

表2

Table 2

表2(Table 2)

表2 刀盘系统前15阶振型和固有频率 Table 2 Natural frequency and first 15 order vibration mode of cutterhead system 振动形式 固有频率/Hz 刚体模态 f1=0 电机、小齿轮 纯扭转振动(重根) f2~9=57 刀盘、大齿圈平移 f10=61,f11=70,f12=114, 倾覆耦合振动 f13,14=120,f15=124

表2 刀盘系统前15阶振型和固有频率 Table 2 Natural frequency and first 15 order vibration mode of cutterhead system

将模态振型正规化后，得到刀盘系统各阶固有频率下的振型矢量如图 4所示，其中自由度编号1~59分别对应系统自由度.

图 4(Figure 4)

Fig. 4

图4 刀盘系统各阶振型 Fig. 4 Vibration modes of cutterheader system

由模态分析结果可知：①刀盘系统第一阶固有振型为刚体模态，所有构件均作无弹性变形的刚体运动；② 刀盘系统振动主要集中在中间阶模态，低阶和高阶相对振动幅值较小；③前15阶固有振型主要为电机和小齿轮的纯扭转振动及刀盘和大齿圈平移倾覆耦合振动，这同实际TBM掘进中刀盘出现的振动形式基本相符^[14]，低阶频率大小分别为57和61Hz，大于小齿轮的转频(1.16Hz)和啮合频率(16.24Hz)等内部激励频率，但可能会与外部激励频率重合，系统有发生共振的危险.

固有频率对参数的敏感度是指固有频率受系统参数影响的灵敏程度，计算方法有矩阵摄动法和导数法.研究固有频率随系统参数的变化，探讨其对质量和刚度的变化敏感度，在设计阶段预测系统的固有特性，通过调节参数使系统避开参数敏感点，获得较好的系统参数设计区间.

本文采用导数法，再运用模态法进行参数的灵敏度分析^{[15, 16]}.通过推导得出第n阶固有频率对刚度和质量参数的敏感度表达式为

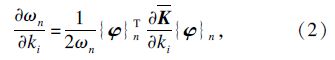
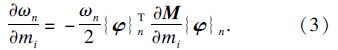
鉴于文章篇幅及研究重点，下面以刀盘分体的结构参数为例，定量分析固有频率及敏感度的影响规律，其余构件的参数影响分析方法类似.

首先设定刀盘分体切向支撑刚度为可变参数，且各分体对应的切向支撑刚度均相等，将刚度矩阵分别对刚度求导后，代入式(2),化简后，则可得固有频率对刀盘分体切向刚度的敏感度：

图 5(Figure 5)

Fig. 5

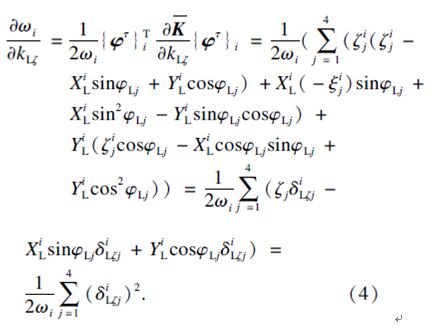
图5 系统固有频率随刀盘分体切向支撑刚度变化情况 Fig. 5 Natural frequency versus tangential stiffness of cutterhead pieces (a)—固有频率; (b)—固有频率灵敏度.

由图 5可知，刀盘分体切向支撑刚度的变化会引起模态振型的变化，即发生模态跃迁现象，以图 5a中的B点(k_Lζi=3.61GN/m)为例，随着刀盘分体切向刚度的微小变动，ω₁₅先为刀盘、大齿圈平移及小齿轮、电机扭转耦合振动模式；ω₁₆为刀盘和大齿圈平移倾覆耦合振动模式，在B点重合后振动模式统一为刀盘、大齿圈平移及小齿轮、电机扭转耦合振动，此时固有频率灵敏度值发生突变(图 5b).这表明B点为系统参数的敏感点，与之类似的还有A(k_Lζi=3.21GN/m)和C(k_Lζi=4.81GN/m)点处，这些点处参数的微小变化会引起振动特性的剧烈改变，在结构设计制造和装配中，需要控制各个边界的刚度参数.

同理，将质量矩阵对刀盘分体质量求导后，代入式(3)，化简可得固有频率对分体质量的灵敏度为

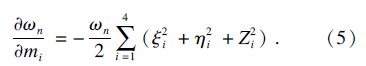
通过计算得出固有频率及灵敏度随刀盘分体质量的变化曲线，如图 6所示.

图 6(Figure 6)

Fig. 6

图6 系统固有频率随刀盘分体质量变化情况 Fig. 6 Natural frequency versus mass of cutterhead pieces (a)—固有频率随分体质量变化； (b)—跃迁点附近的局部放大； (c)—固有频率灵敏度随分体质量变化.

同刚度影响规律类似，通过图 6分析可知，刀盘分体质量变化的跃迁点为13.92，19.14，20.88及22.62t.以 A点为例，随着刀盘分体质量的微小变动，ω₁₄先为刀盘、大齿圈及小齿轮平移振动模式，ω₁₅为刀盘平移振动模式，两条固有频率轨迹迅速靠近至A点重合，之后又迅速分离，振型发生互换，此时固有频率灵敏度值也发生突变(图 6c).在结构设计制造中，需要控制各构件的质量参数，避免落在敏感点处.

1) 刀盘系统的低阶固有振型主要为电机、小齿轮纯扭转振动模态及刀盘、大齿圈平移倾覆耦合振动模态，对应的低阶固有频率为57和61Hz，大于系统内部激励，可能会和外部激励频率重合，系统有发生共振的危险.

2) 刀盘系统振动主要集中在中间阶模态，低阶和高阶相对振动幅值较小.

3) 刀盘分体结构参数主要影响第10~20阶固有频率，且获得刀盘分体切向支撑刚度和质量敏感区间分别为3~4GN/m和 19~23t，其余结构参数分析方法类似，在结构设计制造及装配中，需要合理控制系统参数，尽量避免落在这些敏感点较多的区间.

以上得到的结论在实际TBM刀盘设计时，可根据设计方案预先估算其分体质量及支撑刚度，避免参数落在敏感区间.下一步工作将进行TBM刀盘掘进现场的振动测试，并研制TBM刀盘缩尺模型，开展相关的动力学试验，验证全文动力学模型的正确性.