2.中国矿业大学(北京) 资源与安全工程学院, 北京 100083
2. School of Resources & Safety Engineering, China University of Mining & Technology (Beijing),Beijing 100083, China.
Corresponding author: ZHANG Wen-fen, E-mail: zhangwenfen@163.com
采空区是矿山安全生产所面临的主要灾源之一,准确获取采空区剖面等信息是实施采空区灾害防治及空区周边资源安全开采的重要基础,而采空区模型边界剖面线的提取是实现可视化的前提[1, 2].由于采空区受爆破冲击、失稳破坏等因素的影响,其边界形态往往比较复杂,导致其边界剖面线的提取具有一定的难度.
目前国内外对于三角网格模型剖面轮廓线的提取开展了一些研究,主要形成了三大类方法:紧邻排序法[3, 4, 5],该方法运用交点之间的距离关系进行排序,依次找出距离最近的点进行排序;扇形区域法[6, 7, 8],该方法将所有的交点包含在同一个圆中,将圆划分为若干个扇形区域,找出每个扇形区域中距离圆心最远的点作为边界剖切面上的点,然后一次将扇形区域中的点进行连接形成边界剖面线;传统凸包算法[9, 10, 11],该方法根据所有交点的位置关系,依次找出最外层的包络线,生成三维模型的边界剖面线.
针对三大类边界剖面线提取方法应用于复杂边界采空区时存在的缺陷,提出适用于复杂边界采空区三角网格模型边界剖面线新的提取方法——凸包排序法,旨在获得完整的采空区三角网格模型边界剖面线,准确形成采空区剖面.
1 边界剖面线无序点集的提取三角网格模型是通过大量的三角形对三维实体表面进行离散逼近,在三维空间中围成封闭有界的区域[5].三角网格模型应满足以下几个条件:网格上的每个面片都是三角形;网格上的每条边都为两个三角形所共有.
用垂直于任意坐标轴的平面剖切采空区三角网格模型获取剖面的无序点集.现以z=zi的平面说明其交点获取的方法.三角形与z=zi剖切面的位置关系总共有三种情况,如图 1所示.

|
图1 剖面与三角形相交情况 Fig. 1 Positional relationships between triangle and profile |
1) 三角形的一个顶点位于剖切面上,有一个交点,见图 1a.
2) 三角形的一条边位于剖切面上,有两个交点,见图 1b.
3) 三角形与剖切面相交,有两个交点,见图 1c.
对于图 1a和图 1b两种情况求交点时,只需要判断三角形顶点坐标中的z值是否与剖切面zi的值相等,如果相等则说明顶点为交点;对于图 1c情况,线段p1p2与平面交点为a1,a1距离p1和p2两点的长度比例t为


同理可求出线段p1p2与剖切面zi交点a2的坐标.求出剖切面zi与三角网格模型的所有交点依次标记为{a1,a2,…,ai,…}并将该数据容器记为A,作为生成采空区边界轮廓线的数据容器.
用上述方法求取采空区边界轮廓线的交点是以三角形为判断单元,而形成三角网格模型的每条三角形的边都会为2个三角形所共有.因此求剖切面zi与三角形的交点时,除最先和最后与剖切面相交的三角形与剖切面的交点求了一次以外,其他的交点均求了2次.因此需要删除点集A中的重复点,并将去除重复点后的交点重新保存到数据容器A={a1,a2,…,ai,… ,an}中.以某采空区在zi=-762.365m处的剖面为例,删除重复点之前的交点个数为346,删除重复点之后的交点个数为153.
2 采空区边界线提取方法数据容器A中的交点是按照剖切面与三角网格模型的相交顺序依次保存到数据容器中的.图 2为按照数据容器A中交点求出的顺序依次连接形成的边界轮廓线.因此应先将数据容器A中的交点按照交点的位置进行排序才能连线生成精确的剖面轮廓线.

|
图2 无序点集的剖面图 Fig. 2 Sectional view of unordered points set |
传统的提取采空区三角网格模型边界轮廓线的方法有紧邻排序法[3, 4, 5]、扇形区域法[6, 7, 8].
虽然紧邻排序法及扇形区域法都可以按照一定的规律将采空区三角网格模型的边界轮廓线提取出来,但是这两种方法对于点云比较密集及边界变化较平缓的采空区模型比较适用.实际开采出的采空区大多具有较为明显的凹陷和凸起,当采空区的边界具有较大凸起、凹陷或由于遮挡物的存在等因素时,运用这两种方法形成的采空区的边界轮廓线如表 1所示.
|
|
表1 传统剖面轮廓线提取方法的原理及缺陷 Table 1 Theory and error of traditional profile contour extraction method |
传统的凸包算法[8, 9, 10]是找出数据容器中所有点的最外层凸包,使得所有的点都包络于凸包内.其原理:找出数据容器A={a1,a2,…,ai,… ,an}中x坐标最小的点作为凸包的第一个点记为c1,计算与c1连线与水平方向夹角最大的点,作为凸包的第二个点记为c2;从数据容器A中找出与c1,c2夹角最大的点(c2作为中间点)作为凸包的第三个点记为c3;c2代替c1,c3代替c2,找出夹角最大的点[11, 12, 13, 14, 15];直至形成最外层的包络线,将所有的点均包络其中,如图 3所示.

|
图3 传统凸包算法生成的剖面图 Fig. 3 Profile contour generated with traditional convex hull algorithm |
由图 3可知,凸包算法应用于提取大量散乱点云最外层的包络线时较为精确,但是运用于边界线上交点的排序时,生成最外层的凸包后仍在进行判断,一直基于凸包算法的规则将所有的交点排序连线,生成一圈圈的包络线,这与实际的边界线不符.
针对传统边界线交点排序法存在的缺陷,借助凸 包算法生成的最外层包络线,提出了凸包排序法,将包络于最外层轮廓线内的交点添加到轮廓线中,以解决复杂采空区剖面线交点的排序问题,生成准确的边界剖面轮廓线.
凸包排序法生成边缘轮廓线的基本思想:
1) 找出数据容器A={a1,a2,…,ai,… ,an}中n个数据中横坐标最小的点记为c1,作为生成边缘轮廓线的第一个点.
2) 对于其余的n-1个点,计算与c1连线与水平方向夹角的余弦值,取出余弦值最小的点,作为生成初始边缘轮廓线的第二个点.
3) 对于点集A中其余的n-2个点ai,可构成三角形c1c2ai,找出∠c1c2ai最大的点ai作为生成初始边缘轮廓线的第三个点c3.
4) c2代替c1,c3代替c2,在其余n-3个点中,重复3),寻找下一个生成初始边缘轮廓线的点.
5) 当c3与c1重合时,停止,即生成最外层的包络线,如图 4中的实线所示.

|
图4 z=z0处的边缘轮廓线 Fig. 4 External contour at linez=z0 |
在上述最外层包络线的基础上,有大量的交点在包络线内,要想将所有的交点都添加到边界轮廓线中,有2个不确定性:交点是随机分布的不确定性;添加到边界轮廓线后的完整剖面形态的不确定性,包括交点和轮廓线位置关系的不确定性.因此需要确定边缘轮廓线中交点与轮廓线的位置关系,将所有的交点添加到轮廓线中.
凸包排序法的原理:将边缘轮廓线L1周围的交点添加到剖面线中,首先将b1,b2分别与L1周围的点连线,当边缘轮廓线内的点在L1周围时,b1b2与交点连线形成的夹角为钝角;当b1b2与凸包线L2,L3侧的点(a4,a5,a6,a7)进行连线时形成的夹角为锐角,通过判断夹角的大小确定交点应添加到哪条轮廓线中,如图 5所示.

|
图5 最大张角准则的原理 Fig. 5 Principle of maximum opening angle |
具体步骤如下:
1) 先找出与b1b2形成最大夹角的点,判断三点夹角的公式为
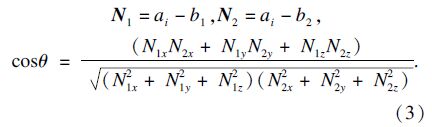
2) 再判断以a2为顶点的夹角是否为钝角,这是因为当点添加到正确的边缘轮廓线中时与b1b2形成的夹角为钝角,否则应将交点添加到其他的初始边缘轮廓线中;用夹角的余弦值判断交点是否满足条件,这是因为余弦值在[0°~180°]为单调递减函数,余弦值取得最小值的点即为夹角最大的点,并且当余弦值为负值时,该夹角为钝角.这样就可以判断点a2是否满足条件,是否应该加入到b1-b2这条边缘轮廓线中.
3) 按照此方法将所有的交点进行判断并添加到相应的边缘轮廓线中,并将排好序的交点进行连线,即可得到剖面轮廓线,图 6为在图 4边缘轮廓线的基础上生成的完整剖面图.

|
图6 z=z0处的完整剖面图 Fig. 6 Complete profile at line z=z0 |
实验表明,基于钝角准则将包络于边缘轮廓线内的其他交点添加到剖面线中,提取出的剖面线精简效果理想,不但保持了采空区边界的细节而且体现了采空区边界的凸起和凹陷,与采空区边界线实际形态吻合度最高.而且对于三角网格模型与剖面交点较少,以及采空区边界发生突变时生成的剖面图与实际也相符,如图 7所示.

|
图7 凸包压入法生成的剖面图 Fig. 7 Profile contours generated by convex hull penetration method |
所提出的凸包排序法应用于具有复杂边界的采空区具有很好的适用性.利用凸包算法的原理生成初始边界剖面线,而不需要对模型建立复杂的拓扑邻接关系;再利用凸包排序法将初始边界轮廓线内的其他交点添加到相应的轮廓线中,形成完整的剖面图,能够很好地表现三维模型的剖面特征.
3 算法应用某铜矿是国内大型深部多金属矿山,多年的开采形成了各种形状复杂的采空区,利用 CMS设备对采空区进行三维探测,获取大量的采空区点云数据,对收集的点云数据进行曲面重建.以52#~16#采场为例形成如图 8a所示的三角网格模型,沿标高方向从-790m到-750m每隔5m进行剖切.根据三角网格模型中三角形与剖切面的位置关系,计算出每一标高位置处构成剖面轮廓线的所有标高线与三角形的交点,对所有交点按照凸包排序法进行排序生成如图 8b所示的边界剖面线.

|
图8 52#~16#采空区剖面图 Fig. 8 Cavity profile at line 52#~16# (a)—三角网格模型; (b)—边界剖面线. |
以z=-586m,x=8616.165m位置的边界线为例,根据凸包排序法生成的采场探测边界剖面线和设计边界剖面线复合模型,可测定采场的具体某一标高位置的超挖和欠挖情况.由图 9(外部线为运用凸包排序法生成的采场探测边界剖面线,内部线为采场设计边界剖面线)可知,采场顶板存在超挖(垮落)现象,超挖距离达到6.0m.进而可有效掌握采空区顶板上部巷道工程的安全状况,从而为矿山进一步改进采场回采技术、施工管理和进行安全监控提供了一种新的可靠手段.

|
图9 采空区剖面边界线与采场设计边界线对比 Fig. 9 Comparison of actual cavity profile and designed stope profile |
此外,按照凸包排序法生成的边界剖面线和微积分的思想,将所有的剖面面积求出,然后乘以上下两剖面之间的距离进行累加,也可求出三维模型的体积.52#~16#采场的体积为54430m3.
4 结 论1) 在分析目前常用的三角网格模型边界剖面线提取方法,即紧邻排序法、扇形区域法和传统凸包算法运用于边界复杂的采空区边界剖面线提取时存在的缺陷的基础上,研究改进了传统的凸包算法,形成了适用于复杂边界采空区三角网边界剖面线的新提取方法——凸包排序法.
2) 凸包排序法成功地克服了传统方法的缺陷,能很好地反映复杂采空区边界的细节,有效地实现了复杂采空区边界剖面线的生成,具有实际工程应用价值,从而为矿山实施采空区灾害防治及空区周边资源安全开采提供重要的技术支持.
| [1] | Zuo H Y ,Luo Z Q,Guan J L,et al.Multi-disciplinary design optimization on production scale of under-ground metal mine[J].Journal of Central South University:English Edition,2013,20(5):1332-1340.( 1) 1) |
| [2] | 罗周全,刘晓明,张木毅,等.大规模采场三维探测及回采指标可视化计算[J].中南大学学报:自然科学版,2009,40(6):1732-1736. (Luo Zhou-quan,Liu Xiao-ming,Zhang Mu-yi,et al.Stope 3D monitoring and its mining index visible calculation[J].Journal of Central South University:Science and Technology,2009,40(6):1732-1736.)( 1) 1) |
| [3] | Sayeed M D.Classifying facial expressions using level set method based lip contour detection and multi-class support vector machines[J].International Journal of Pattern Recognition and Artificial Intelligence,2011,25(6):835-862.( 2) 2) |
| [4] | 李明珠,卢章平,徐扬,等.基于最小距离的NURBS曲线的形状混合方法[J].工程图学学报,2008,29(4):96-101. (Li Ming-zhu,Lu Zhang-ping,Xu Yang,et al.An approach to shape blending of NURBS curves based on minimum distance[J].Journal of Engineering Graphics,2008,29(4):96-101.)( 2) 2) |
| [5] | Zhen L.Three-dimensional modeling of tracer experiments to determine gas trapping in foam in porous media[J].Energy & Fuels,2010,24(5/6):3239-3250.( 3) 3) |
| [6] | 陈俊智,侯克鹏.利用OpenGL对岩体三维模型进行切剖面方法研究[J].云南冶金,2005,34(1):12-15,20. (Chen Jun-zhi,Hou Ke-peng.Study on three-dimension rock body cutting method using OpenGL[J].Yunnan Metallurgy,2005,34(1):12-15,20.)( 2) 2) |
| [7] | 曾峦,顾大龙.一种基于扇形区域分割的SIFT特征描述符[J].自动化学报,2012,38(9):1513-1519. (Zeng Luan,Gu Da-long.A SIFT feature descriptor based on sector area partitioning[J].Acta Automatica Sinica,2012,38(9):1513-1519.)( 2) 2) |
| [8] | 李凤云,李沛谕,高福祥,等.基于扇形区域的无线传感器网络位置隐私保护[J].东北大学学报:自然科学版,2013,34(1):21-24,34. (Li Feng-yun,Li Pei-yu,Gao Fu-xiang,et al.Location privacy protection for wireless sensor networks based on fan-shaped region[J].Journal of Northeastern University:Natural Science ,2013,34(1):21-24,34.)( 3) 3) |
| [9] | Liu G H,Chen C B.A new algorithm for computing the convex hull of a planar point set[J].Journal of Zhejiang University:English Edition,2007,8(8):1210-1217. ( 2) 2) |
| [10] | Lee S H ,Lee S M,Sohn Y,et al.Fuzzy entropy design for non convex fuzzy set and application to mutual information[J].Journal of Central South University:English Edition,2011,18(1):184-189.( 2) 2) |
| [11] | Yuan P,Tian Y J,Zhou Y J,et al.Convex decomposition based cluster labeling method for support vector clustering[J].Journal of Computer Science and Technology,2012,27(2):428-442.( 2) 2) |
| [12] | Geng Y F,Wang Z L.A coastal ocean model of semi-implicit finite volume unstructured grid[J].China Ocean Engineering, 2012,26(2):277-290.( 1) 1) |
| [13] | Graham R L.An efficient algorithm for determining the convex hull of a finite planar set [J].Information Process Letter(S0020-0190),1972,1(5):132-133.( 1) 1) |
| [14] | Shevtsov M,Soupikov A,Kapustin A,et al.Highly parallel fast KD-tree construction for interactive ray tracing of dynamic scenes[J].Computer Graphics Forum,2007,26(3):395-404.( 1) 1) |
| [15] | Chen C L.Computing the convex hull of a simple polygon[J].Pattern Recognition(S0031-3203),1989,22(5):561-565. ( 1) 1) |







