Corresponding author: TANG Jin-huan, E-mail: tangjinhuan-hot@163.com
从战略、战术和运作层面对生产-分销系统的集成研究日趋重要,众多研究结果表明其在很大程度上优于一般的解耦方法[1, 2].目前从这3个层次上对生产-分销系统的研究主要分为3种类型:①战略协调,研究工厂、分销中心选址及客户需求分配问题;② 战术协调,对库存分配-分销策略问题的研究;③ 运作一体化,集成生产-库存-运输的研究.而第三个层面被认为是与实际问题联系最紧密、方案最精确、角度最契合的研究方法[3, 4, 5, 6, 7].本文基于运作一体化这一视角对三层生产-分销系统中的最优批量策略展开研究.
目前大多数成果都是基于以下2个假设:①供应链中最上游企业的需求能够瞬时得到满足,不存在任何短缺;②产品从供应链上游流向下游的过程中,持有成本不断升高[8, 9].本文针对3层生产-分销系统的批量策略进行研究,主要特色体现在4个方面:①允许生产-分销系统中各级成员的持有成本随意变动;②突破以往只有制造商和销售商的两层生产-分销系统的范畴;③定义了一个绩效对比标准;④使用中石油东北石化销售公司的部分数据作为算例的来源,算例的结果及灵敏度分析验证了本文的有效性及在理论和实践上的意义.
1 问题描述与条件假设 1.1 问题描述本文研究了由1个生产商(M),N个区域配送中心(RDC)和K个分销商(D)构成的三层生产-分销系统,如图 1所示.生产商以一定的批量对RDC补货,RDC以一定的批量对分销商进行点对点补货,通过对流入流出RDC的最优经济批量的控制,使得系统总成本最小.

|
图1 3层生产-分销系统结构图 Fig. 1 Structure of 3-stages production-distribution system |
1) 生产商存在有限的生产率c,持有成本由M,RDC,D三方共同承担.
2) 生产-分销系统的上层到下层单位产品单位距离的运输成本是固定的.
3) 每个RDC都存在差异化容量限制.
4) RDC和D的补货过程遵循( Qj,Rj)库存策略.
5) RDC层的进出库可能同时发生,且生产-分销系统的成本体现为RDC进出库过程及其库存持有状况,其他不影响批量决策的成本可不予考虑.
2 模型构建在研究生产-分销系统固定批量策略时,现有库存水平为连续的锯齿状模型,如图 2所示,故生产-分销系统的成本来自生产商和销售商的持有成本,以及RDC的选址成本.设RDC(t)为t时刻RDC的库存水平.

|
图2 Tin=5,Tout=3时库存水平的锯齿状模型 Fig. 2 Jagged model of inventory at Tin = 5,Tout=3 |
Tin和Tout表示RDC的入库和出库批量,在时间点t,入库流量为Tin$\left\lfloor {1 + t/{T_{{\text{in}}}}} \right\rfloor $,出库流量为Tout$\left\lfloor {1 + t/{T_{{\text{out}}}}} \right\rfloor $,初始库存W(0)为Tin$\left\lfloor {1 + t/{T_{{\text{in}}}}} \right\rfloor $-Tout$\left\lfloor {1 + t/{T_{{\text{out}}}}} \right\rfloor $+W(0),单位产品持有成本为h时,可得RDC的总持有成本为0.5h(Tin+Tout-2Tin∧Tout),进而可得在批量策略(Tin,Tout)下,系统的总成本为
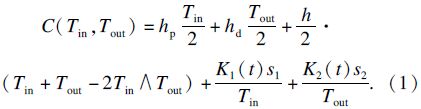
3.1 固定批量策略与多重批量策略的推导
定义1 如果Tin=bp,Tout=pq,p,q是素数, b=Tin∧Tout,则Tin和Tout之间存在一个最大公约数b.故(Tin,Tout)到(p,q)可以看作是在不同的时间基准上的移动.该方法适用于一切有理数的情况.
首先在固定批量策略制定时,对于一个给定的时期比,可得b=Tin∧Tout的最优值.设
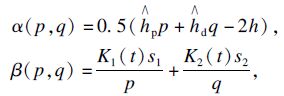
则(1)式可改写为
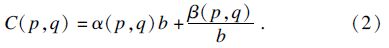
由式(2)知,对任意(p,q),b有唯一的最优值b*(p,q)= $\sqrt {\beta \left( {p,q} \right)/\alpha \left( {p,q} \right)} $,可得,最优成本 C*=2 $2\sqrt {\alpha \left( {p,q} \right)/\beta \left( {p,q} \right)} $.
可见,(p,q)给出了一组唯一的基于时间基准的简化策略Ρ(p,q),定义生产-分销系统成本最小化的策略为Ρ(p*,q*),且原始批量策略(Tin*,Tout*)与Ρ(p*,q*)一致.令φ(p,q)= α(p,q)β(p,q),则生产-分销系统的最优成本C*(Tin*,Tout*) = $2\sqrt {\varphi \left( {p,q} \right)} $.
在q=1时,简化的最优成本为
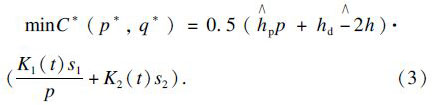
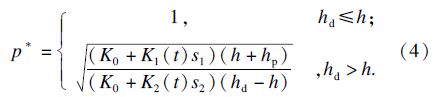
同理,可得p=1时的最优策略,考虑到简化后的成本函数具有凸性,则多重混合批量策略为
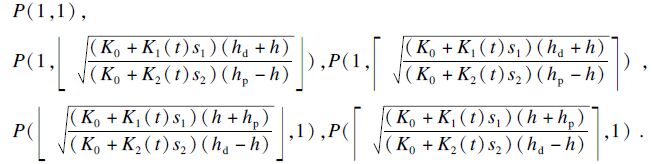
首先,引入最优批量比值r*和一种假设的情况I0,I0为绩效对比的标准,含有参数hp 0,h0和hd 0,以及运输成本K1(t)s1和K2(t)s2,r(I)为情形I最优批量的比值,即 $r*\left( I \right) = \frac{{T{*_{{\text{in}}}}}}{{T{*_{{\text{out}}}}}}$.
定理1 r*$ \notin $(1,2)时,不适用多重策略;当p*=1或q*=1时,固定策略的结果等价于多重策略;当r*≥2时,因为要满足不等式$\frac{{C\left( {p,q} \right)}}{{C\left( {p*,q*} \right)}} \leqslant \frac{{f\left( {p/q} \right)}}{{f\left( {r*} \right)}}$,推导可得固定策略的成本比多重策略高1.03 % ,而当r*≤1时,结论与r*≥2一致.
证明 令生产商的持有成本为hp 0 = ${\hat h_{\text{p}}}$= hp+h,RDC的持有成本为h0=0,分销商的持有成本为hd0 = hd+h,如此3层生产-分销系统分解为2层,分别对其两端使用EOQ公式可得此时的最优策略 (Tin,Tout)为$T_{{\text{in}}}^0 = \sqrt {2{K_1}\left( t \right){s_1}/{h_{\text{p}}}} $,$T_{{\text{out}}}^0 = \sqrt {2{K_2}\left( t \right){s_2}/{h_{\text{d}}}} $.此时生产-分销系统的总成本为C0=K1(t)s1+K2(t)s2+hdTout/2+hTin/2.I0在策略Ρ(p,q)下,令
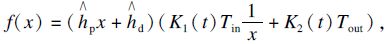
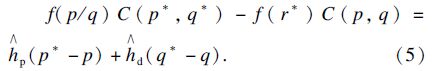
4.1 计算实验算例
本文以中石油东北化工销售分公司生产-分销系统实际运作中的部分数据作为算例来源.大连生产基地向公司区域配送中心华北大区进行产品调运,华北大区RDC再向北京、天津、石家庄、保定、沧州这些区域内的分销商进行配送.数据参数如表 1所示.
|
|
表1 实验参数 Table 1 Experiment parameters |
传统方法下生产-分销系统的总成本为17418万元[7],而本文的最优策略下的成本为15562万元,比传统的批量策略节省了1856万元.
4.2 灵敏度分析为了进一步检验本文优化策略,以下针对关键变量平均运价和持有成本进行灵敏度分析.
图 3表明,随着平均运价的增长,一般传统策略下总成本的增幅要比最优批量策略下的成本增幅缓慢.图 4表明,随RDC单位产品持有成本的增加,传统的批量策略下成本增长缓慢,而最优批量策略在RDC持有成本小于0.2时,增长也比较缓慢,且成本要远远小于传统策略,当持有成本超过0.2后,成本急剧增加,直到持有成本达到0.6后,最优批量策略失效.可见最优批量策略的实施需要考虑具体的问题,不是在所有的情况下都是有效的.

|
图3 平均运价对总成本的影响 Fig. 3 Effect of average rate on total cost of freight |

|
图4 RDC持有成本对总成本的影响 Fig. 4 Effect of RDC holds cost on total cost |
本文也对RDC持有成本h和分销商持有成本hd同时变化的3层生产-分销系统的传统策略和最优批量策略进行了分析,如图 5和图 6所示.

|
图5 随持有成本变化的生产-分销成本 Fig. 5 Production-distribution cost varied with holding cost |

|
图6 批量策略下随持有成本变化的生产-分销成本 Fig. 6 Production-distribution cost varied with holding cost in lot-sizing policy |
图 5说明传统意义上随着h和hd的增大,系统的成本呈稳定上升趋势,但是在使用最优批量策略时(图 6),随着两级库存成本的变化,系统的成本呈现先下降后上升的趋势,可见最优批量策略的绩效取决于生产-分销系统中RDC和分销商的持有成本状况.这也是管理者应予以重视的区域.
5 结 语本文对3层生产-分销系统的批量策略进行研究,给出了不同情景下企业批量策略的选择,并以中石油东北化工销售公司的运营数据作为算例分析的来源,结果证明使用本文所提的批量策略相比于传统的方法在成本节约上具有明显的优势.本研究是针对随机需求下单一产品的批量策略问题,对于多产品多阶段的复杂情况的探讨将是下一步的研究方向.
| [1] | Park Y B.An integrated approach for production and distribution planning in supply chain management[J].International Journal of Production Research,2005,43(6):1205-1224.( 1) 1) |
| [2] | Amorim P,Günther H O,Almada-Lobo B.Multi-objective integrated production and distribution planning of perishable products[J]. International Journal of Production Economics,2012,138(1):89-101. ( 1) 1) |
| [3] | Chen Z L.Integrated production and outbound distribution scheduling:review and extensions[J].Operations Research,2010,58(1):130-148.( 1) 1) |
| [4] | Clark A J,Scarf H.Optimal policies for a multi-echelon inventory problem [J].Management Science,2004,50(12):1049-1052.( 1) 1) |
| [5] | 戢守峰,曹楚,黄小原.基于CPFR的协同补货方法[J].东北大学学报:自然科学版,2007,28(7):1049-1052. (Ji Shou-feng,Cao Chu,Huang Xiao-yuan.Collaborative replenishment policies based on CPFR[J].Journal of Northeastern University :Natural Science,2007,28(7):1049-1052.)( 1) 1) |
| [6] | Amorim P,Belo-Filho M A F,Toledo F M B,et al.Lot sizing versus batching in the production and distribution planning of perishable goods[J]. International Journal of Production Economics,2013,146(1):208-218.( 1) 1) |
| [7] | Kutzner S C,Kiesmüller G P.Optimal control of an inventory-production system with state-dependent random yield[J]. European Journal of Operational Research,2013,227(3):444-452.( 2) 2) |
| [8] | Zhou W.RFID and item-level information visibility[J].European Journal of Operational Research,2009,198(1):252-258.( 1) 1) |
| [9] | Varthanan P A,Murugan N,Kumar G M.A simulation based heuristic discrete particle swarm algorithm for generating integrated production-distribution plan[J].Applied Soft Computing,2012,12(9):3034-3050.( 1) 1) |




