摩擦是无处不在的自然现象,且往往与振动相互联系,工程和日常生活中由摩擦引起的自激振动现象是非常普遍的,精密机床(例如,磨床,坐标镗床,数控机床)的工作台、溜板等移动部件的低速进给运动可能导致工作台的摩擦自激振动,即爬行,而高速切削运动又能导致刀具和工件的摩擦自激振动,即切削颤振,摩擦自激振动破坏了机床的准确性和连续性,使响应出现削顶、死区和突变等现象,降低跟踪精度,严重影响工件表面加工精度、表面粗糙度和定位度,甚至产生废品和事故[1].
为了加强控制系统的精度,减轻甚至消除摩擦造成的危害,近几十年来国内外越来越多的学者开始对摩擦自激振动展开了研究[2, 3, 4],Elmer[5]研究了没有阻尼和不同摩擦模型时质量块-带的黏滑和纯滑动振动,提供了黏滑和纯滑动振动之间转换的表达式.Thomse[6]建立了一个典型的摩擦模型,然后给出了一个非线性摩擦模型的黏滑振动不同运动形式的幅值、频率的近似表达式,接着用摄动分析方法给出了滑动阶段和黏滑阶段的时间间隔,最后得出只要动静滑动摩擦系数相差不大,就能避免黏滑运动.Madeleine[7]研究了一个两自由度的质量-阻尼-弹簧系统在受到间歇加载时的摩擦激振现象.黄毅等[8]建立了双质体-传送带模型,通过数值仿真方法分析了系统内共振对干摩擦自激振动的影响.
本文通过建立含有Stribeck模型的典型质体-弹簧-传送带摩擦自激振动模型,并由李雅普诺夫判据对系统平衡点进行分析,确立了系统临界失稳速度,并通过理论计算出临界黏滑速度,然后通过数值仿真的方法分析各参数对系统稳定性的影响,最后总结出提高系统稳定性的措施.本文对摩擦自激振动系统的研究,对促进摩擦振动耦合动力学的发展、研究和解决由摩擦而产生的动力学问题具有重要的价值.
1 摩擦自激振动系统模型的建立质体-弹簧-传送带的系统模型常用于分析机械进给系统的黏滑运动,质量块m以常速v运行在传送带上,固定端与刚度为k的弹簧和阻尼系数为c的阻尼器连接,质量块和带之间的摩擦力F为质量块提供驱动力.
 | 图 1 质体-弹簧-传送带自激振动系统模型 Fig. 1 Model of the friction self-excited vibration system of plastid-spring-conveyor belt |
本文采用的是摩擦系数与运动速度的Stribeck曲线模型,用来描述一般机械部件运动结合面之间的摩擦行为[9],该摩擦模型的表达式为

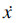 -v0表示质量块和带之间的相对速度;μs,μm分别为静动摩擦系数;vm是对应于最小动摩擦的速度,μs≥μm.质量块初始速度为零,即vr=0,当质量块开始滑动时,摩擦力随着速度的增加开始是逐渐减小,随后又开始逐渐增加.
-v0表示质量块和带之间的相对速度;μs,μm分别为静动摩擦系数;vm是对应于最小动摩擦的速度,μs≥μm.质量块初始速度为零,即vr=0,当质量块开始滑动时,摩擦力随着速度的增加开始是逐渐减小,随后又开始逐渐增加.
建立Stribeck摩擦自激振动系统的动力学方程为

引入下列无量纲变量: ,τ=ω0t,X=xk/N,2β=cω/k,将F=μN代入式(2),并将式中的量进行无量纲化后可简化为
,τ=ω0t,X=xk/N,2β=cω/k,将F=μN代入式(2),并将式中的量进行无量纲化后可简化为

式(3)即为该摩擦自激振动系统的无量纲动力学模型.
2 临界失稳速度和黏滑速度的确定为了便于进行稳定性分析,由常微分方程理论可知,正规型高阶微分方程可以化为等价的一阶微分方程组,可将式(3)写为一阶微分方程组如式(4)所示:

当系统中输入速度很大时,质量块在摩擦力和弹簧力的作用下处于静平衡状态[10],并且平衡时满足 .摩擦系数表达式中的符号函数sgn(vr)=-1,系统参数分别取如下值:μs=0.4,μm=0.25,vm=0.5m/s,通过李雅普诺夫稳定性理论对系统平衡点稳定性进行分析.
.摩擦系数表达式中的符号函数sgn(vr)=-1,系统参数分别取如下值:μs=0.4,μm=0.25,vm=0.5m/s,通过李雅普诺夫稳定性理论对系统平衡点稳定性进行分析.
由方程(4)取 求得系统的平衡点:
求得系统的平衡点:

将式(4)的右边展开成泰勒级数,略去二次以上的项,得到系统的一次近似方程,求出一次近似微分方程在X1=0,X2=0处,相对变量X1,X2的雅可比矩阵如下:

取系统无量纲参数β=0.01,代入式(6),得到矩阵A对应的特征方程为

式(7)可化为典型的特征方程:

根据Hurwits定律可知,系统临界失稳速度可以通过p=0求解出来:p=0.44-1.8v20=0,得到系统的临界失稳速度为:v0=vb1=0.4944m/s.
进给系统中临界黏滑速度[11]的计算公式为

本文中μs=0.4,μm=0.25,c1+c2=2β=0.02,k=1,m=0.05,将参数代入式(9),得到该系统的临界黏滑速度为0.4372,当进给速度低于0.4372时,质量块黏滞在带上,此时它进行的是黏滑振动;当进给速度在0.4372~0.4944m/s之间时,质量块的最小相对速度不为零,此时它进行的是纯滑动振动.因此,系统进行的运动也是两种振动形式:一种是纯滑动振动,它存在的进给速度区间很小;另一种是黏滑运动,在一个周期内既存在滑动又存在黏滞阶段.
3 不同参数对系统动力学稳定性的影响 3.1 进给速度对系统稳定性的影响分析仿真系统初始参数设定为:β=0.01,μs=0.4,μm=0.25;初始条件设置为:X=0,=0,将进给速度参数分别设定为0.76,0.54,0.48,0.44,0.36m/s,对系统进行仿真,捕捉特征相图如图 2所示,其对应的Poincare截面图如图 3所示,其中,vb1=0.4944m/s,vb0=0.4372m/s.
 | 图 2 不同进给速度下的相图 Fig. 2 The phase diagram of different feed speed (a)—v0=0.76 m/s >vb1; (b)—v0=0.54 m/s >vb1; (c)—v0=0.48 m/s∈[vb0, vb1]; (d)—v0=0.44 m/s∈[vb0, vb1]; (e)—v0=0.36 m/s < vb0. |
 | 图 3 不同进给速度下对应的Poincare截面图 Fig. 3 The corresponding Poincare sectional view of different feed speed (a)—v0=0.48 m/s∈[vb0, vb1]; (b)—v0=0.44 m/s∈[vb0, vb1]; (c)—v0=0.43 m/s∈[vb0,vb1]; (d)—v0=0.36 m/s∈[vb0, vb1]; (e)—v0=0.1 m/s < vb0. |
由图 2和图 3可以看出,随着带速的不同,系统响应的数值仿真结果也不同.以两个临界速度vb0=0.4372 m/s和vb1=0.4944 m/s为界分析系统的运动状态,可将系统运动分为以下3个阶段:当带速v0>vb1=0.4944时,系统将稳定在平衡点X,且进给速度越大,系统的稳定性越好;当带速v0< vb1时,系统的平衡点发生失稳,开始产生自激振动,该过程可以分成两个阶段,开始阶段即vb0< v0< vb1时,摩擦自激振动为纯滑动形式,其相图为不存在黏滞阶段的极限环,这时质量块和带之间的最小相对速度始终不为零;后一阶段即v0< vb0=0.4372m/s时,自激振动为黏滑运动形式,极限环中出现比较明显的黏滞阶段.从系统Poincare截面图可以看出,当速度比较低时,系统进行的是准周期运动,即表明纯滑动和黏滑运动都属于准周期运动.
3.2 阻尼系数对系统稳定性的影响分析系统初始参数设定为:μs=0.4,μm=0.25,vm=0.5m/s;初始条件设置为:X=0,=0;取β=0.02,0.06,0.6对整个系统进行仿真,来观察阻尼系数对系统的影响.捕捉特征相图如图 4所示.
 | 图 4 不同阻尼系数下的相图 Fig. 4 The phase diagram of different damping coefficients (a)—β=0.02; (b)—β=0.06; (c)—β=0.6. |
从图 4可以看出,随着系统阻尼的增大,系统的运动黏滞阶段所占的比例越来越小;当增大到一定程度的时候,黏滞阶段消失,系统开始进行稳定的纯滑动运动;当阻尼再次增大到一个临界值时,系统开始稳定在平衡点,所以,在一定程度上增大系统的阻尼可以抑制自激振动的发生,从而提高系统运动的稳定性.
3.3 不同刚度对系统稳定性的影响分析系统初始参数设定为:β=0.01,μs=0.4,μm=0.25m/s,vm=0.5m/s,取k=1,4,8,20,40,对整个系统进行仿真,来观察刚度对系统的影响,捕捉特征相图如图 5所示,其对应的Poincare截面图如图 6所示.
 | 图 5 不同刚度下的相图 Fig. 5 The phase diagram of different stiffness (a)—k=1; (b)—k=4; (c)—k=8; (d)—k=20; (e)—k=40. |
 | 图 6 不同刚度下的Poincare截面图 Fig. 6 The Poincare sectional view of different stiffness (a)—k=1; (b)—k=4; (c)—k=8; (d)—k=20; (e)—k=40. |
从图 5和图 6可以看出,随着刚度的增大,系统的黏滞阶段所占的比例越来越小,当刚度增加到一定程度的时候,黏滞阶段消失,系统开始进行稳定的纯滑行运动,并且纯滑动阶段对应的极限环也随着刚度的增大逐渐减小.所以在一定程度上提高系统的刚度可以缩短黏滞阶段的运动,从而提高系统运动的稳定性.
3.4 不同动、静摩擦差值对系统稳定性的影响分析系统初始参数设定为:β=0.01,vm=0.5m/s,k=1,动、静摩擦差值分别取值为0.01,0.02,0.05,0.1,0.2,对系统进行仿真,观察动、静摩擦差值对系统的影响,捕捉特征相图如图 7所示.
随着动、静摩擦差值越来越小,轨迹也逐渐呈螺旋状向中间一点聚集,表明系统逐渐从不稳定状态向稳定状态变化.从相图可以发现,差值越大,则响应的振动幅值也越大,并在v0=vb0时达到了最大值;并且差值越小,黏滞阶段所占的总极限环比例也逐渐减小,在达到一定程度的时候,黏滑振动会消失,转化为稳定的纯滑动运动.
 | 图 7 不同动、静摩擦差值下的相图 Fig. 7 The phase diagram of different dynamic and static friction coefficient (a)—μs=0.4, μm=0.2; (b)—μs=0.4, μm=0.3; (c)—μs=0.4, μm=0.35; (d)—μs=0.4, μm=0.38; (e)—μs=0.4, μm=0.39. |
1) 本文建立了基于Stribeck摩擦模型的质体-弹簧-传送带的自激振动动力学模型,通过李雅普诺夫稳定性判据对系统平衡点做稳定性分析,获得系统临界失稳速度为0.4944m/s,通过理论公式获得系统临界黏滑速度为0.4372m/s.
2) 从仿真结果可以看出,低速状态下的自激振动可分为两个阶段:当v0< 0.4372 m/s时,自激振动形式为黏滑运动形式;当0.4372m/s < v0<0.4944m/s时,自激振动为纯滑动形式,这两种运动均为准周期运动.
3) 随着进给速度、阻尼和刚度的增大、动、静摩擦差值的减小,系统的黏滞阶段所占的比例减小;当达到一定程度的时候,黏滞阶段消失,系统开始进行稳定的纯滑动运动.
4) 通过比较各参数对系统稳定性的影响知,进给速度影响系统的运动状态是影响系统稳定性的主要因素.
| [1] | Okan B, Omer A.Computer simulation of stick-slip motion in machine tool slideways[J]. Tribology International, 2004, 37(4):347-351.( 1) 1) |
| [2] | Leine R I, Van Campen D H, de Kraker A, et al.Stick-slip vibrations induced by alternate friction models[J]. Nonlinear Dynamics, 1998, 6(1):41-54.( 1) 1) |
| [3] | Andreaus U, Casini P.Dynamics of friction oscillators excited by a moving base and/or driving force[J]. Journal of Sound and Vibration, 2001, 245(4):685-699.( 1) 1) |
| [4] | 张有强, 丁旺才.两自由度干摩擦振动系统黏滑运动分析[J]. 振动与冲击, 2013, 32(7):184-187. (Zhang You-qiang, Ding Wang-cai.Stick-slip vibration analysis for a 2-DOF dry friction vibration system[J]. Journal of Vibration and Shock, 2013, 32(7):184-187.)( 1) 1) |
| [5] | Elmer F J.Nonlinear dynamics of dry friction[J]. Journal of Physics A:Mathematical and General, 1997, 30(17):6057-6063.( 1) 1) |
| [6] | Thomse J J, Fidlin A.Analytical approximations for stick-slip vibration amplitudes[J]. International Journal of Non-Linear Mechanics, 2003, 38(3):213-224.( 1) 1) |
| [7] | Madeleine P.New limit cycles of dry friction oscillators under harmonic load[J]. Nonlinear Dynamic, 2012, 70(2):1435-1443.( 1) 1) |
| [8] | 黄毅, 王太勇, 李强, 等.干摩擦系统的自激振动数值研究[J]. 机械强度, 2008, 30(4):539-543. (Huang Yi, Wang Tai-yong, Li Qiang, et al.Numerical study on self-excited vibrations of a dry-friction system[J]. Journal of Mechanical Strength, 2008, 30(4):539-543.)( 1) 1) |
| [9] | Feeny B F, Moon E C.Chaos in a forced dry-friction oscillator:experiments and numerical modeling[J]. Journal of Sound and Vibration, 1994, 170(3):303-323.( 1) 1) |
| [10] | 刘素华.三维和四维非线性系统Hopf分岔反馈控制[D]. 长沙:湖南大学, 2008. (Liu Su-hua.Feedback control of Hopf bifurcation in two classes of nonlinear high dimensional systems[D]. Changsha:Hunan University, 2008.)( 1) 1) |
| [11] | 龚庆寿.进给爬行时临界驱动速度的计算与分析[J]. 机床与液压, 2004(6):110-114. (Gong Qing-shou.Analyzing and calculating the critical driving velocity before climbing phenomenon[J]. Machine Tool & Hydraulics, 2004(6):110-114.)( 1) 1) |




