由于硬涂层可在高温、高腐蚀环境下减少薄壳结构的振动响应,而受到越来越广泛的关注[1, 2, 3].为了更好地实施硬涂层阻尼减振,需要获得硬涂层的减振机理,即涂敷硬涂层后结构件振动响应减少的原因,进而实施硬涂层减振优化设计.现有的关于硬涂层减振机理研究,多集中于微观材料学[4, 5, 6],且多数学者认为硬涂层微观颗粒之间的内摩擦是硬涂层能够减振的原因.但是,完全基于材料学研究硬涂层的减振机理是不够的,还需要从宏观振动学的角度,创建硬涂层复合结构的动力学分析模型,进而研究硬涂层的减振机理.
创建可以真实表征硬涂层复合结构动力学特性的分析模型需要基于大量振动实验的结果,包括涂层前后结构件的固有频率、阻尼、振动响应等参数.但是,相对于固有频率、振动响应的测试,目前还无法较为准确地获取结构件的阻尼[7].通用的做法仍是基于瑞利阻尼假设,由半功率带宽法[8]或自由振动衰减法[9]获得结构件的阻尼比.这种测试手段获得的阻尼是一个综合性指标,包含了多种阻尼成分.由于无法有效分离硬涂层的阻尼贡献,致使创建硬涂层复合结构减振机理分析模型变得非常困难.
本文以基础激励作用下的硬涂层悬臂梁为对象,从分离硬涂层的阻尼贡献出发,创建了硬涂层悬臂梁复合结构减振机理的分析模型.首先,对涂层前后的悬臂梁系统进行了减振特性试验,获得了固有频率、阻尼比、振动响应等参数;然后,在对涂层前后悬臂梁系统储能及耗能分析的基础上,确定了获取硬涂层材料阻尼贡献的方法;最后,基于Oberst梁理论,创建了同时考虑材料阻尼和黏性阻尼的悬臂梁系统减振机理分析模型,并用实验校验了分析模型的正确性.
1 涂层前后硬涂层悬臂梁减振实验这里以单面涂敷NiCrAlY硬涂层的悬臂钛梁为例(见图 1),测试涂层前后悬臂梁固有频率、阻尼比、振动响应.梁的几何及材料参数见表 1.实验系统见图 2,梁以悬臂的方式装夹(夹持区为25mm),测试装置包括LMS采集前端、金盾EM-1000F电磁振动台和B&K4517轻质加速度传感器等.选用轻质加速度传感器可以尽量减少附加质量的影响,拾振点为距离夹持区100mm处.
 | 图 1 涂敷NiCrAlY的悬臂梁 Fig. 1 Cantilever beam with NiCrAlY coated |
| 表 1 钛基悬臂梁及涂层的几何及材料参数 Table 1 Geometrical and material parameters of titanium beam and hard coating |
 | 图 2 悬臂梁振动特性测试系统 Fig. 2 The system of testing the cantilever beam dynamic characteristic |
采用振动台扫频激励获得悬臂梁的固有频率,其中涂层前后前5阶固有频率见表 2.采用半功率带宽法获得各阶模态阻尼比,相关结果见表 3.以共振频率激励试件,激励幅度为1g(这里g为重力加速度),测试获得悬臂梁的共振响应,相关结果见表 4.
| 表 2 涂层前后悬臂梁的固有频率 Table 2 The natural frequencies of uncoated and coated beam |
| 表 3 涂层前后悬臂梁的模态阻尼比 Table 3 Modal damping ratios of uncoated and coated beam |
| 表 4 涂层前后悬臂梁的振动响应 Table 4 The vibration response of uncoated and coated beam |
从测试结果可以看出,涂敷NiCrAlY硬涂层后悬臂梁系统各阶模态损耗因子均增加,而振动响应显著降低,表明硬涂层具有减振效果.
2 涂层前后悬臂梁储能及耗能分析图 2所描述的是基础激励作用下处于稳态振动的悬臂梁系统.设Ub为涂层前悬臂梁系统一个周期内存储的能量,可表示为

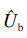 为最大应变能;
为最大应变能;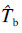 为最大动能.而Db为涂层前一个周期内消耗的能量,可表示为
为最大动能.而Db为涂层前一个周期内消耗的能量,可表示为


模态损耗因子是模态阻尼比的2倍,即


相应的Ds为涂层后系统一个周期内消耗的能量,表示为


同样,在共振状态时,有


设R=Uc/U′b为储能比,则式(9)可变为

参照式(1)储能比又可以表示为最大应变能比或者最大动能比,因而可设

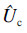 和
和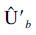 分别为硬涂层和基体的最大应变能;
分别为硬涂层和基体的最大应变能;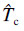 和
和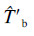 分别为硬涂层和基体的最大动能.因此硬涂层复合结构总的应变能及动能可表示为
分别为硬涂层和基体的最大动能.因此硬涂层复合结构总的应变能及动能可表示为



式(14)中的动能之比又可以表示为质量之比,即


可见只要获得涂层前后复合结构各阶固有频率、涂层与基体的厚度和密度等参数就可以获得储能比,进而代入到式(10)获得硬涂层材料对应各阶次的损耗因子.
4 硬涂层悬臂梁减振机理分析模型的建立及振动响应分析 4.1 基础激励硬涂层梁的解析分析模型图 2所示的基础激励悬臂梁系统,可用图 3所示的力学模型来描述.
 | 图 3 基础激励作用下的涂层梁 Fig. 3 The hard-coating beam under base excitating |
按照Oberst梁理论[10],可得硬涂层悬臂梁在基础激励作用下的解析分析方程,即

以下用所创建的模型分析第1部分实验所对应的悬臂梁涂层前后拾振点的响应,以校验上述分析模型的正确性.根据式(10)可获得硬涂层对应于各阶次的材料阻尼.分析模型中的基础激励幅度仍为1g,拾振点与实验相对应(x=0.1m处)可得到涂层后悬臂梁的振动响应.相关结果均列在表 5,表 6中.
| 表 5 悬臂梁前5阶的储能比R和硬涂层材料阻尼ηc Table 5 The first 5-orders storage energy ratios and hard-coating material damping |
| 表 6 实验与分析获得涂层梁共振响应的对比 Table 6 Vibration response comparison between experiment and analytical analysis of the coated cantilever beam |
1) 对单面涂敷NiCrAlY硬涂层的悬臂梁振动特性进行了测试,结果显示涂层后复合梁的阻尼系数增加、振动响应降低,表明该硬涂层具有阻尼减振效果.
2) 通过对涂层复合结构的储能及耗能分析,进一步利用损耗因子的定义,可以将硬涂层的阻尼贡献从测试的阻尼值中分离出来.
3) 剔除硬涂层贡献的阻尼,可用涂层前的阻尼值来代替,实践表明这并不会带来很大的分析误差.
4) 利用分离出的硬涂层材料阻尼以及涂层前测试获得的阻尼,可创建用于模拟实际涂层梁系统动力学特性的解析分析模型.
| [1] | Blackwell C, Palazotto A, George T J, et al.The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007, 14(1):37-51.( 1) 1) |
| [2] | 杜广煜, 谭祯, 巴德纯, 等.电弧离子镀制备 NiCrAlY 涂层及其阻尼性能[J]. 东北大学学报:自然科学版, 2012, 33(5):727-730. (Du Guang-yu, Tan Zhen, Ba De-chun, et al.Preparation and damping properties of NiCrAlY coating by arc ion plating[J]. Journal of Northeastern University:Natural Science, 2012, 33(5):727-730.)( 1) 1) |
| [3] | Reed S A, Palazotto A N, Baker W P.An experimental technique for the evaluation of strain dependent material properties of hard coatings[J]. Shock and Vibration, 2008, 15(6):697-712.( 1) 1) |
| [4] | Torvik P J.A slip damping model for plasma sprayed ceramics[J]. Journal of Applied Mechanics, 2009, 76(6):061018.( 1) 1) |
| [5] | Tassini N, Patsias S, Lambrinou K.Ceramic coatings:a phenomenological modeling for damping behavior related to microstructural features[J]. Materials Science and Engineering A, 2006, 442(1):509-513.( 1) 1) |
| [6] | Abu Al-Rub R K, Palazotto A N.Micromechanical theoretical and computational modeling of energy dissipation due to nonlinear vibration of hard ceramic coatings with microstructural recursive faults[J]. International Journal of Solids and Structures, 2010, 47(16):2131-2142.( 1) 1) |
| [7] | Srikantha Phani A, Woodhouse J.Viscous damping identification in linear vibration[J]. Journal of Sound and Vibration, 2007, 303(3):475-500.( 1) 1) |
| [8] | Torvik P J.On estimating system damping from frequency response bandwidths[J]. Journal of Sound and Vibration, 2011, 330(25):6088-6097.( 1) 1) |
| [9] | Magalhães F, Cunha Á, Caetano E, et al.Damping estimation using free decays and ambient vibration tests[J]. Mechanical Systems and Signal Processing, 2010, 24(5):1274-1290.( 1) 1) |
| [10] | 刘棣华.黏弹性阻尼减振降噪技术[M]. 北京:宇航出版社, 1990. (Liu Di-hua, Viscoelastic damping vibration noise reduction technology[M]. Beijing:Aerospace Press, 1990.)( 1) 1) |




