2. 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142
2. Information Engineering School, Shenyang University of Chemical Technology, Shenyang 110142,China.
Corresponding author: WANG Guo-zhu, E-mail: wang.guo.zhu@163.com
故障检测的实质可以用数据分类的问题来描述,通常数据可以分为正常(目标)样本与非正常(非目标)样本,在实际生产过程中,得到正常状态下的过程数据是很容易的,运用所获得的正常数据来对实时数据进行监视,是数据驱动故障检测的重要手段[1].SVDD方法是一种利用最小封闭球体与支持向量理论进行数据描述的方法,此方法与支持向量机类似,是一种针对小样本的学习理论[2, 3],其主要思想是通过寻找数据集合最小边缘半径的超球体,使其能够尽可能包含所有的同类数据,排除非同类数据,达到数据合理分类的目的.该方法是一种新的单值分类方法,可以运用于工业过程故障检测.因此,可以利用正常数据建立SVDD模型,求取模型控制限并对新的过程采样进行检测,实现过程监视的目的.
本文在SVDD算法的基础上,提出一种稀疏性SVDD(S-SVDD)建模方法,用于解决前者不能较好地处理大样本数据缺陷的问题.经过理论推导与仿真实验,验证了此方法可以有效地应用于工业过程故障检测.
1 SVDD方法与稀疏性理论介绍SVDD理论上要求一个包含所有目标数据的尽可能小的球体,与SVM[4]类似,这个球体由少部分支持向量决定.对于一个有限数据集,支持向量是位于高维数据分布边缘的少量样本,SVDD[3, 5]根据结构风险最小化原理,通过求取一个尽可能少的包含奇异点数据,并且体积最小的球体来描述样本数据,即求满足一定条件的半径为R和球心为a的球体.此方法适用于处理非线性与非高斯数据[6].
1.1 支持向量数据描述(SVDD)为建立一个非线性数据模型,SVDD方法首先通过一个非线性变换  :x→F将原始正常数据 X={xi∈ R d,i=1,2,…,n} 映射到一个高维特征空间;其次,在特征空间中寻找一个最小体积的球体并使其包含所有的高维空间数据点.SVDD求取最小超球体的实质就是求解以下最优化问题[1]:
:x→F将原始正常数据 X={xi∈ R d,i=1,2,…,n} 映射到一个高维特征空间;其次,在特征空间中寻找一个最小体积的球体并使其包含所有的高维空间数据点.SVDD求取最小超球体的实质就是求解以下最优化问题[1]:




根据上面分析求取使L最小值情况下的最优解αi,可以表现为以下三种情况(xsv为支持向量):

当αi=0,数据点在球体内;当αi=C,数据点在球体外;当0<αi<C,数据点在超球体表面上.

对于新采样的无故障数据只需满足以下条件:

连续过程采集到的数据点具有一定的稀疏性,并且它们之间的距离通常具有相似性,当把数据映射到高维特征空间后,数据点之间稀疏程度会更加明显.
一个高维数据点x的稀疏度定义如下:



定理:样本点x的稀疏度越大,其在高维空间中距离SVDD球心的距离越远.
假设原始数据中有两个样本点x1与x2,并且






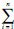 αiαjk(xi,xj)为常数,因此
αiαjk(xi,xj)为常数,因此


SVDD超球体是利用在所有样本中选取的支持向量来建立的,因此在建模之前要对所有数据点进行预判断,找出支持向量.对大样本数据而言,这样会经过很多不必要的步骤,既影响建模速度,又对建模精度不利.而在实际工业过程中,数据收集量往往非常庞大,为了及时检测到系统中是否存在故障,建模以及检测时间在一定程度上起到了关键作用.本文提出的S-SVDD方法是在数据稀疏度的基础上,选择稀疏度大的局部数据(超球体外层数据)样本进行SVDD超球体建模,可以弥补SVDD方法的不足.
S-SVDD建模及检测步骤如下:首先,对训练样本集合 X={xi∈Rd,i=1,2,…,n},根据1.2节求取各个采样时刻数据的稀疏度δ(xi);第二,选择稀疏度大的前k个采样数据,并利用这些数据建立SVDD模型,求取超球体球心、半径;第三,对于新的采样数据,根据式(7)计算其到球心的距离Dnew,Dnew<R为正常采样,否则发生故障.
3 仿真实验TE过程由压缩机、分离器、反应器、冷凝器和汽提塔5个主要的操作单元组成,包括A~H 8种成分,过程中有41个测量变量和12个控制变量.详细描述与工艺流程参见文献[10, 11, 12].仿真实验选取22个测量变量和11个控制变量作为监测样本集,数据通过仿真软件获得.各个工况的采样间隔均为3 min,每次运行时间为48 h,仿真开始时系统处于正常状态,在8 h时引入故障.正常工况的960个样本采自过程平稳运行状态,各故障工况前160个时刻为无故障样本,后800个时刻为故障样本.TE过程共有21种故障,表 1对其中的故障f2,f4,f13,f14进行了详细的描述.为了比较两种方法的仿真结果,其参数设置见表 2.
| 表 1 TE过程故障描述 Table 1 Faults description of TE process |
| 表 2两种方法的参数设置 Table 2 Parameters of two methods |
首先对正常过程的960个样本进行标准化处理,使用传统SVDD方法进行建模,计算正常状态的球心a和半径R,分别对21组故障数据进行监视,找到故障发生时刻,部分检测结果如图 1所示.
 | 图 1 SVDD方法的故障检测结果 Fig. 1 Fault detection results using SVDD method (a)—f2; (b)—f4; (c)—f13; (d)—f14. |
根据原始正常数据分布在高维映射空间内的稀疏特性,选取前100个高维分布边缘的数据点进行S-SVDD建模,找到最优的球心a和半径R,并求取新的采样数据距离球心a的距离,对应检测结果见图 2.
 | 图 2 S-SVDD方法的监视结果 Fig. 2 Fault detection results using S-SVDD method (a)—f2; (b)—f4; (c)—f13; (d)—f14. |
从TE过程故障f2,f4,f13和f14的检测结果可以看出:两种方法都可以及时检测到故障以及确定故障的发生时刻,但对比二者的建模与各个故障的检测时间,S-SVDD方法有明显的改善.具体建模及检测各故障情况耗时见表 3.
| 表 3 对4种故障的定量分析比较 Table 3 Comparison of quantitative analysis on the four kind of faults |
本文引入数据分布在高维映射空间内的稀疏性,并根据此特性选取前k个高维分布边缘的数据点进行S-SVDD建模,经过理论推导和仿真,验证了S-SVDD建模方法可以有效地提高建模和过程检测速度,减少冗余计算量;对样本量较大的数据集可以利用筛选后的小样本建模,在一定程度上改善了SVDD方法处理大样本数据计算耗时的问题.
| [1] | 谢磊,刘雪芹,张建明,等.基于NGPP-SVDD的非高斯过程监控及其应用研究[J].自动化学报,2009,35(1):107-112.(Xie Lei,Liu Xue-qin,Zhang Jian-ming,et al.Non-Gaussian process monitoring based on NGPP-SVDD[J].Acta Automatica Sinica,2009,35(1):107-112.)( 3) 3) |
| [2] | Vapnik V N.统计学习理论[M].北京:电子工业出版社,2004.(Vapnik V N.Statistical learning theory[M].Beijing:Electronic Industry Press,2004.)( 1) 1) |
| [3] | Tax D,Duin R. Support vector data description[J].Machine Learning,2004,54(1):45-66.( 2) 2) |
| [4] | Vapnik V N.The nature of statistical learning theory[M].New York:Springer-Verlag,1995.( 1) 1) |
| [5] | Tax D.One-class classification[M].Delft:Delft University of Technology,2001:21-55.( 1) 1) |
| [6] | Ge Z Q,Gao F,Song Z H.Batch process monitoring based on support vector data description method[J].Journal of Process Control,2011,21:949-959.( 1) 1) |
| [7] | Saitoh S.Theory of reproducing kernels and its applications[M].Harlow:Longman Scientific & Technical,1998.( 1) 1) |
| [8] | Asa B H,David H,Siegelmann H T,et al.Support vector clustering[J].Journal of Machine Learning Research,2001,2:125-137.( 1) 1) |
| [9] | Wang X M,Chung F L,Wang S T.Theoretical analysis for solution of support vector data description[J]. Neural Networks,2011,24:360-369.( 1) 1) |
| [10] | Lee J M,Yoo C K,Choi S W,et al.Nonlinear process monitoring using kernel principal component analysis[J].Chemical Engineering Science,2004,59:223-234.( 1) 1) |
| [11] | Yu J,Qin S J.Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models[J].AICHE Journal,2008,54:1811-1829.( 1) 1) |
| [12] | Lee J,Kang B,Kang S.Integrating independent component analysis and local outlier factor for plant-wide process monitoring[J].Journal of Process Control,2011,21:1011-1021.( 1) 1) |




