Corresponding author: CUI Xiao-yu, E-mail: cuixy@bmie.neu.edu.cn
按照使用相机的数量,立体视觉可以分为多相机系统和单相机系统两大类.现有的基于棱镜的单相机立体视觉算法可简单归结为两种:一种是利用“虚拟相机”的概念,将图像平面捕获的图像认为是两部或者多部“虚拟相机”拍摄而成[1,2,3],按照传统的标定算法,首先标定出虚拟相机的位置,然后进行匹配和重建;另一种是将棱镜参数化,根据光线追迹或者几何光学的思想计算光的传播路径,最终得到图像的极线几何关系,从而进行匹配和重建[4, 5, 6, 7].
第一种方法原理简单,可以使用现有的关于多相机的立体视觉算法实现.然而,这种方法在标定的过程中仅使用镜头的非线性畸变模型,没有考虑因为棱镜的引入和棱镜摆放位置的误差所带来的非线性畸变,所以“虚拟相机”方法不是一套完整精确的理论模型.第二种方法较为直观,因为计算的是实际的光路或者实际的像点,可以避免棱镜引入的非线性畸变.然而,这种方法所得结果的准确程度与棱镜的位置紧密相关.但在实际应用中,很难精确掌握棱镜的放置位置,棱镜的实际位置往往会和假设位置有一定的偏差,必然会影响到三维重建结果的稳定性和准确性.
本文针对现有两种模型方法上存在的不足,通过单相机标定所得的空间点和图像平面上投影点的对应关系,把棱镜的位置参数和透视投影的过程相结合,将解棱镜位置参数的问题转化为非线性最优化的问题.最后利用差分进化算法解出参数.
1 棱镜折射的透视投影变换 1.1 单相机的透视投影变换按照Zhang[8]的相机标定模型,单相机的投影变换过程为

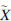 为物体点在世界坐标系下的坐标;
为物体点在世界坐标系下的坐标;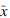 为投影点在图像平面上的坐标;Mint表示相机的内部参数矩阵;Mext表示相机的外部参数矩阵,即旋转平移矩阵;s为一个任意的比例因子.
1.2 棱镜折射的几何光学模型
为投影点在图像平面上的坐标;Mint表示相机的内部参数矩阵;Mext表示相机的外部参数矩阵,即旋转平移矩阵;s为一个任意的比例因子.
1.2 棱镜折射的几何光学模型
根据文献[8, 9, 10],空间一点经棱镜折射后所成的虚像点可以由以下公式表示:

如果将棱镜折射后的虚像点作为单相机投影变换中的物体点,根据式(1)可得

将式(1),(2)和(3)合并可得

该方程表示了基于棱镜的立体视觉系统在相机坐标系下一点到图像平面的投影变换过程.
2 棱镜的参数化简本文将棱镜的参数分为内参数和外参数两种.内参数在棱镜出厂时均已确定.而外参数是根据棱镜的摆放位置的改变而不同,理论上需要包含18个参数(3个点坐标和3个方向向量).由于参数过多,会影响计算的速度和精度,而且十分容易得到具有二义性的位置结果.这18个参数间存在着内部联系,所以本文根据棱镜的内参数所表示的3个平面的位置关系,将这些参数化简为6个.求出这6个参数,即可得到棱镜的全部外参数.
2.1 坐标系建立本文根据该系统在实际应用中的情况,建立的坐标系如图 1所示.
 | 图 1 坐标系的建立和光线从空间点到图像平面的折射变换 Fig. 1 Coordinate system and the refraction of ray from one point to the image plane (a)—俯视图;(b)—侧视图. |
如图 1b所示,设棱镜后平面MNBA的单位法向量为VB(vbx,vby,vbz),设向量 V(vx,vy,vz)与VB垂直,同时平行于UD并且方向向上.设棱镜的左右侧平面MUDA,NBDU的法向量分别为VR(vrx,vry,vrz),VL(vlx,vly,vlz),这两个平面可以认为是向量VB绕着轴V旋转而得到.

设棱镜的棱UD与平面y=0的交点为E(ex,0,ez),点E在平面MUDA和NBDU上,过点E向后平面MNBA做垂线,与后平面交点设为Q(qx,qy,qz),根据直线方程和两点距离公式,可得方程组:

根据前两节的化简,表示棱镜位置的参数可归纳为

POS表示棱镜位置参数的一个集合.设三维空间中物体点的个数为n,在不考虑遮挡等干扰因素的情况下,投影到相机图像平面上点的个数为2n.棱镜的位置估计过程可以表示为函数最小化问题:

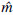 (Mint,Mp,Mext,Xi)表示在相机坐标系下空间一点Xi到图像平面的投影过程;xij表示点Xi在第j个图像平面的投影点坐标.因为有左右两个图像平面,所以j的取值为1和2.根据式(4)和式(7),可以将式(8)转化为
(Mint,Mp,Mext,Xi)表示在相机坐标系下空间一点Xi到图像平面的投影过程;xij表示点Xi在第j个图像平面的投影点坐标.因为有左右两个图像平面,所以j的取值为1和2.根据式(4)和式(7),可以将式(8)转化为

在实际情况下,事先不可能无误差地测量出棱镜与相机的相对位置,即没有一个准确的棱镜位置参考值.本文首先使用计算机模拟的方法,人为设置一组数据,来评估提出算法的可行性和准确性;然后使用实际数据的实验方式与现有方法进行比较,证明本文方法在计算精度上的优越性.
3.1 实验过程1) 拍摄标定板图像.相机位置固定,移动标定板在空间中的位置,并且分别拍摄同一位置下未放置棱镜和放置棱镜两种情况下的图像.
2) 相机标定.利用相机图像先标定出相机的内外参数.
3) 根据相机标定的结果,分别对10幅放置棱镜时捕获的图像进行畸变矫正,得到校正后无相机镜头畸变的图像.
4) 标定棱镜位置.利用校正后的棱镜图像找到对应点的图像坐标,根据前一步找到的空间坐标,通过式(9)和差分进化算法计算棱镜的位置.
5) 根据计算出的棱镜位置,将相机坐标系下的三维坐标重新投影到图像平面,计算与实际点的误差.
6) 利用计算出的棱镜位置,对三维空间点进行重建.在相同的条件下,按照现有的光线追迹和虚拟相机的方法进行三维重建,比较重建结果.
3.2 实验结果与分析表 1为使用本文方法迭代400次时,利用所得到的棱镜位置参数,计算三维空间点的重投影误差所得结果.计算过程在相机坐标系下进行,其中,距离误差表示重投影点和实际点在图像平面上的绝对距离,像素误差为距离误差乘以单位像素的尺寸.从表 1中可以看出,本文提出的方法在计算重投影点方面具有很高的精度,平均像素误差小于0.5个像素.这一点对计算极线几何的方法十分重要.因为误差很小,可以极大地提高计算极线的准确度,从而降低匹配过程的难度,提高匹配的精度.
| 表 1 使用迭代400次时所得棱镜位置计算空间点到图像平面的重投影误差 Table 1 The reprojection errors when using the parameters of prism which obtained by 400 times iterations |
表 2为在同一条件下,光线追迹、虚拟相机和本文提出的方法距离重建的结果对比.可以看出,虚拟相机的方法误差最大,因为棱镜的位置误差以及棱镜的畸变和普通相机的镜头畸变有很大的区别.相机的镜头畸变都会有一个光学中心,图像以这个光学中心为基准,呈桶形或者枕形的变形.而在引入棱镜之后,整幅图像的畸变不是以一点为基准,而是以靠近中心的一条直线为基准,而且这种畸变对虚拟相机方法的影响会随着距离的增加而降低.光线追迹的方法也很容易受到棱镜位置误差的影响,因为该方法完全使用参数化的棱镜位置进行光线的计算,略微的偏差都会直接影响到这个方法的重建精度.在实际放置棱镜位置时,总会有一定的误差存在.这种影响会使三维重建的结果很不稳定,而且重建误差也会随着物体距离的增加而增加.本文提出的方法实际上是在光线追迹的基础上加入了棱镜位置估计这一步骤.通过一系列的迭代计算,找到棱镜在相机坐标系中的实际位置.在此基础之上进行匹配和重建计算,精度会有很大幅度的提高.
| 表 2 三种方法重建结果比较 Table 2 Reconstruction results by three methods |
因为棱镜制作工艺的问题,包括棱镜角度、材质折射率和棱镜各个平面的位置很难完全量化为精确的参数.本文使用非线性最优化的方法,可以减少这方面问题所带来的误差,但是不可能完全避免误差.而且光线追迹的方法是将单位像素的光线简化为单条光线,在三维重建的过程中只能使用两条光线公垂线的中点作为重建结果,这一过程也会产生误差.使用本文方法可以在3 m的范围内将这些误差控制在4 mm,可以满足大多数视觉系统的需求.
4 结论1) 本文提出的方法弥补了以往基于棱镜的立体视觉方法仅仅根据理想的棱镜位置计算空间点坐标的不足,进一步减小误差.
2) 由于推导过程基于几何光学,所以算法不受棱镜大小的影响,可以将其应用于小体积的棱镜和相机.
3) 只需在初始配置时标定相机的内外参数和棱镜的位置参数,即可将任意相机拍摄的二维图像升级为三维图像,通过三维重建获得拍摄物体点的三维空间信息.
4) 本文的算法增加了棱镜立体视觉的实际应用范围,但基于棱镜的立体视觉技术还是存在一些问题.今后的工作将重点研究如何利用棱镜的位置信息,对棱镜折射产生的畸变进行图像校正以及如何获取稠密视差图.
| [1] | Gao Q,Wang H P,Wang J J.A single camera volumetric particle image velocimetry and its application[J].Science China Technological Science,2012,55(9):2501-2510.( 1) 1) |
| [2] | Genovese K,Casaletto L,Rayas J A,et al.Stereo-digital image correlation measurements with a single camera using a biprism[J].Lasers Engineer,2013,51(2):78-85.( 1) 1) |
| [3] | Cui X Y,Lim K B.A prism-based single-lens stereovision system:from trinocular to multi-ocular[J].Image and Vision Computing,2007,25(11):1725-1736.( 1) 1) |
| [4] | Wu L F,Zhu J G,Xie H M.A modified virtual point model of the 3D DIC technique using a single camera and a bi-prism[J].Measurement Science & Technology,2014,25(11):283-287.( 1) 1) |
| [5] | Erol A,Bebis G,Nicoescu M,et al.Vision-based hand pose estimation:a review[J].Computer Vision and Image Understanding,2007,108(1/2):52-73.( 1) 1) |
| [6] | Zhao M J,Lim K B,Wei L K.Geometrical-analysis-based algorithm for stereo matching of single-lens binocular and multi-ocular stereovision system[J].Journal of Electronic Science and Technology,2012,10(2):107-112.( 1) 1) |
| [7] | Cui X Y,Lim K B,Guo Q Y,et al.Accurate geometrical optics model for single-lens stereovision system using a prism[J].Journal of Optical Society of America A,2012,29(9):1828-1837.( 1) 1) |
| [8] | Zhang Z Y.A flexible new technique for camera calibration[J].Applied Optics,2013,52(1):182-187.( 2) 2) |
| [9] | Chen C Y,Deng Q L,Sun W S.Panoramic stereo photography based on single-lens with a double-symmetric prism [J].Optical Express,2013,21(7):8474-8482.( 1) 1) |
| [10] | 郭方,王克逸,闫佩正,等.用于大视场目标定位的复眼系统标定[J].光学精密工程,2012,20(5):913-920.( 1) 1) |




