Corresponding author: ZHANG Yu, E-mail: yeahzhangyu@126.com
弹性流体动力润滑接触是诸如轴承、齿轮、凸轮等机械结构部件中普遍存在的一种接触状态.润滑接触中的摩擦力对机械构件的系统表现和使用寿命有着重要的影响，因此摩擦的计算是机械构件润滑接触条件下优化设计的关键一步[1].
自Grubin和Vinogradova成功地实现了对弹性流体动力润滑油膜厚度的预测以来，润滑状态的摩擦行为也吸引了众多学者的广泛关注[2].然而对于摩擦的计算并不成功，实际的拖动测试表明流体具有牛顿型流变属性将会明显地高估润滑状态下的摩擦系数[2]，因此近年来学者们采用非牛顿流变属性预测润滑状态下的摩擦系数.Li等[3]，Xu等[4]对非牛顿弹性流体动力润滑和混合润滑状态下齿轮啮合的摩擦系数进行了研究，讨论了影响摩擦系数的相关因素.Seabra等[5]采用干接触状态下的赫兹应力分布作为润滑状态下的油膜压力，计算了非牛顿弹流润滑状态下滚子轴承中滚动体与滚道接触的摩擦系数.崔金磊等[6]分析了钢制接触副在冲击载荷下的瞬态弹流润滑问题，探讨了润滑剂的流变属性、温度等因素对摩擦系数的影响.
总结以上的工作，针对滚动轴承润滑状态下摩擦的研究相对较少，对影响摩擦系数因素的讨论更是有限.本文采用非牛顿弹性流体动力润滑模型，对深沟球轴承滚动体与滚道椭圆接触的润滑问题进行了计算，讨论了粗糙表面、滑滚比、接触力以及滚动速度等因素对轴承摩擦的影响.
1 点接触弹性流体动力润滑 1.1 本构模型采用Ree-Eyring双曲正弦本构模型描述流体的非线性黏性流变行为，本构方程可表述为[7]
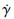为润滑剂的剪切应变率；τ0为参考应力，大于该值时，流体的剪切行为呈现非线性，当τ0趋近于无穷大时，流体为牛顿流；η为润滑剂黏度；τ为黏性剪切应力.
1.2 控制方程
点接触瞬态弹性流体动力润滑问题的雷诺方程可表示为
润滑区域的油膜厚度方程为
润滑剂的黏压力关系由Roelands[10]提出的方程来表示:
在较高压力作用下，油膜的密度发生改变，Dowson-Higginson[11]的油膜压力与密度关系为
润滑区域上油膜压力的总和应等于施加的接触力，具体表示为
考虑到滚动体与滚道润滑区域的油膜较薄，且滚动体与滚道的滚动方向为润滑油的主要流动方向，油膜的剪切应变率可近似认为是常数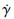，=(u2-u1)/h，因此通过式(1)可以计算剪切应力，
摩擦系数为摩擦力与接触力的比值：
本文以深沟球轴承滚动体与滚道椭圆接触润滑问题为研究对象，如图1所示，a与b分别表示依据赫兹理论计算得到的椭圆接触区域的半轴长.滚动体与滚道接触点处沿滚动方向和垂直滚动方向的当量曲率半径分别为6.276 9 mm和114.75 mm，椭圆率为6.621 7，当量弹性模量为2.274 7×1011 Pa，润滑油属性参见文献[12],环境黏度η0为9.6×10-2 Pa·s,黏压系数α为1.82×10-8 N-1·m2,参考应力τ0=18×106 Pa.采用多网格方法[13]求解润滑区域上的油膜厚度与油膜压力，为了分析网格结构对数值解精度的影响，首先采用最密集层的网格密度分别为257×2 049和257×1 025两种网格布局对接触力为1 000 N，滚动速度为5 m/s，且纯滑动(滑滚比SR=2)条件下的油膜厚度进行了计算，计算得到的中心油膜厚度均为9.805 4×10-7 m，最小油膜厚度分别为8.430 2×10-7 m和8.430 6×10-7 m，两种网格密度几乎给出了相同的计算结果.然而第一种网格布局计算时间是第二种网格布局计算时间的4倍多，因此本文选用第二种网格布局计算油膜厚度与油膜压力.
 | 图 1 深沟球轴承中滚动体与滚道的椭圆接触 Fig. 1 The ball element and raceway elliptical contact in deep grove ball bearing |
为了讨论粗糙表面对轴承摩擦系数的影响，需要获得滚动体与滚道的表面粗糙度以及具体的几何形态(即表面峰谷的几何高度)，数值模拟生成粗糙表面是一个实用且有效的方法.这里采用Patir[14]提出的数值方法生成均方根粗糙度R(下文简称粗糙度R)分别为0.1 μm和0.2 μm，表面峰谷高度符合高斯分布的粗糙表面样本，样本量均为15，以X=1，2，…，15分别表示第1个，第2个直至第15个样本.计算中认为滚动体表面光滑，滚道表面是粗糙的.为了检测润滑界面上是否存在金属接触，首先计算光滑表面在接触力为1 000 N，滚动速度分别为5和10 m/s，滑滚比为2(纯滑动)稳态润滑状态下的最小油膜厚度，分别为8.43×10-7 m和1.26×10-6 m.当表面粗糙度为0.1 μm时，所有15个粗糙表面样本中，表面峰值高度均小于8.43×10-7 m和1.26×10-6 m，因此润滑表面不会发生金属接触.当表面粗糙度为0.2 μm时，所有粗糙表面样本中表面峰值高度均小于1.26×10-6 m，但部分样本中个别表面峰值高度达到甚至略微超过8.43×10-7 m，然而通过作者的检查，这些峰值高度并不在最小油膜厚度的区域，并且也小于所在区域的油膜厚度.因此，无论滚动体与滚道接触表面粗糙度是0.1 μm或者0.2 μm，整个接触表面处于弹流润滑状态，并无金属接触存在.
图2给出了滚动体与滚道润滑表面在接触力为1 000 N，滚动速度分别为5和10 m/s，滑滚比为2，粗糙度分别为0.1和0.2 μm(各15个表面样本)时摩擦系数的计算结果，摩擦系数的统计结果列于表1.结合图2和表1可以看出，对于每一种粗糙度与速度组合的工况，计算得到的15个摩擦系数的变异系数较小，这表明粗糙度一定时，不同粗糙表面之间，表面几何形态(表面峰谷的几何高度)的差异对摩擦系数的影响较小.
 | 图 2 不同表面粗糙度时摩擦系数的比较 Fig. 2 Comparison of friction coefficients for different surface roughness |
 | 表 1 不同工况下摩擦系数的统计结果 Table 1 Statistical result of friction coefficients for different running conditions |
图2中的虚直线与实直线表示滚动速度分别为10和5 m/s时光滑表面的摩擦系数，分别为0.138 5和0.134 5.与粗糙表面摩擦系数的对比可以看出，当速度一定时，光滑表面的摩擦系数最大，粗糙度为0.1 μm表面的平均摩擦系数次之，粗糙度为0.2 μm表面的平均摩擦系数最小，但总体而言三者差距甚微(两种滚动速度条件下，三者差距均不足1%)，这表明在弹流润滑状态下，粗糙度的变化对摩擦系数的影响不大.对滚动速度为5 m/s，粗糙度为0.2 μm的15个不同粗糙表面处于名义接触区域(干接触状态下滚动体与滚道的实际接触区域)以内的油膜厚度的平均值进行了统计，并与光滑表面油膜厚度的平均值进行了比较，结果表明粗糙表面的平均油膜厚度(1.07×10-6 m)大于光滑表面的平均油膜厚度(1.05×10-6 m)，这应该是粗糙表面摩擦系数略小于光滑表面摩擦系数的主要原因.
另外，滚动速度为10 m/s时，润滑表面的摩擦系数大于滚动速度为5 m/s时的摩擦系数，这说明速度的提高引起摩擦系数的增加.
2.2 滑滚比对摩擦系数的影响图3表示的是接触力为1 000 N，滑滚比从0.1(滑滚状态)提高到2.0(纯滑动)，轴承滚动体与滚道润滑表面摩擦系数的计算结果.轴承的运行工况分为三种①滚动速度为5.0 m/s，表面粗糙度为0.2 μm；②滚动速度为5.0 m/s，接触界面光滑；③滚动速度为2.5 m/s，接触界面光滑.这里需要指出的是，对于工况①，粗糙表面以一定的速度从润滑区域的进口滚入，接触界面处于瞬态润滑状态，粗糙表面每移动一个网格的距离计算一次油膜厚度与压力.为了避免润滑界面出现金属接触的情况，并考虑到表面几何形态差异对摩擦系数的影响较小，从生成的粗糙度为0.2 μm的15个表面形貌样本中选取最大表面峰值小于8.43×10-7 m(该值为光滑润滑界面在滚动速度为5.0 m/s,滑滚比为2.0条件下的最小油膜厚度，如上文所述)的一个样本作为分析对象.在每个滑滚比条件下，当粗糙表面完全通过润滑区域后，粗糙表面继续移动10个网格距离，计算每移动一个网格距离时界面的摩擦系数，并且以这10个摩擦系数的平均值作为该滑滚比条件下的摩擦系数.
 | 图 3 滑滚比对摩擦系数的影响 Fig. 3 The influence of slide to rolling ratio on friction coefficient |
从图中可以看出，三种工况条件下的摩擦系数均随着滑滚比的提高而增大，滑滚比较小时摩擦系数增大速率较快，随着滑滚比的提高增大速率减慢，滑滚比为2.0时摩擦系数达到最大值，摩擦系数的变化趋势表明摩擦系数对滑滚比的变化非常敏感，特别当滑滚比较小时，敏感程度尤为显著.摩擦系数随着滑滚比的提高而增大的特点可归因于界面滑动速度的增加以及由此导致的油膜厚度的降低，计算结果表明，对于工况②处于名义接触区域内的油膜厚度的平均值从滑滚比为0.1时的1.09×10-6 m降至滑滚比为2.0时的1.05×10-6 m.从剪切应力的计算公式(10)可以看出，滑动速度的增加以及油膜厚度的降低起到了增大剪切应力的作用，因此引起表面摩擦系数增大.
另外与2.1节纯滑动状态下的规律类似，在滑滚状态下(滑滚比小于2)，粗糙表面(工况①)的摩擦系数也略小于光滑表面(工况②)的摩擦系数.对于光滑表面，相同滑滚比时，滚动速度越大(工况②中的滚动速度大于工况③中的滚动速度)，摩擦系数越大.
2.3 接触力与滚动速度对摩擦系数的影响图4给出了三种滚动速度条件下，滑滚比为0.05时，接触力从200 N增加至1 000 N，光滑表面稳态润滑状态下摩擦系数的计算结果.从图中可以看出，三种滚动速度条件下，摩擦系数随接触力的变化规律十分相似，随着接触力的增加,摩擦系数增大，但增大速率均逐渐减慢.表2给出了接触力从200 N增加至1 000 N，三种滚动速度条件下摩擦系数的差值结果，表中符号μi,j表示滚动速度为i m/s时润滑界面的摩擦系数与滚动速度为j m/s时摩擦系数的差值.任意两种滚动速度条件下，摩擦系数的差值随着接触力的增加逐渐减小，而并非保持恒定，这暗示了当润滑界面的滑滚比恒定时，滚动速度影响摩擦系数随接触力的变化趋势.
 | 图 4 摩擦系数随接触力的变化规律 Fig. 4 Variation of friction coefficient with the contact force |
| 表 2 三种滚动速度条件下摩擦系数的差值 Table 2 The difference of friction coefficient for three different rolling speeds |
1) 滚动速度一定时，粗糙表面的摩擦系数略小于光滑表面的摩擦系数，但二者差距不大.粗糙度一定时，不同粗糙表面间，表面几何形态(即表面峰谷的几何高度)的差异对摩擦系数影响较小.
2) 滑滚比的变化对摩擦系数的影响显著，特别当滑滚比较小时，摩擦系数对滑滚比的变化极为敏感.
3) 摩擦系数随着接触力的增加而增大，但增大速率逐渐减慢.
4) 接触力与滑滚比一定时，滚动速度的提高导致摩擦系数增大.滚动速度对摩擦系数随接触力的变化趋势有一定的影响.
| [1] | Dama R,Chang L.An efficient and accurate calculation of traction in elastohydrodynamic contacts[J].Wear,1997,206(1/2):113-121.( 1) |
| [2] | Brandao J A,Meheux M,Seabra J H O,et al.Traction curves and rheological parameters of fully formulated gear oils[J].Proceedings of the Institution of Mechanical Engineers,Part J:Journal of Engineering Tribology,2011,225(7):577-593.(1) |
| [3] | Li S,Kahraman A.A method to derive friction and rolling power loss formulae for mixed elastohydrodynamic lubrication[J].Journal of Advanced Mechanical Design,Systems,and Manufacturing,2011,5(4):252-263.(1) |
| [4] | Xu H,Kahraman A,Anderson N E,et al.Prediction of mechanical efficiency of parallel-axis gear pairs[J].Journal of Mechanical Design,2006,129(1):58-68.(1) |
| [5] | Seabra J,Sottomayor A,Campos A.Non-Newtonian EHL model for traction evaluation in a roller-inner ring contact in a roller bearing[J].Wear,1996,195(1/2):53-65.(1) |
| [6] | 崔金磊,杨萍,杨沛然.基于瞬态弹流润滑问题的热效应及非牛顿效应分析[J].润滑与密封,2013,38(2):18-22.(Cui Jin-lei,Yang Ping,Yang Pei-ran.Analysis of thermal effect and non-Newtonian effect based on transient elastohydrodynamic lubrication[J].Lubrication Engineering,2013,38(2):18-22.)(1) |
| [7] | Chapkov A D,Venner C H,Lubrecht A A.Roughness amplitude reduction under non-Newtonian EHD lubrication conditions[J].Journal of Tribology,2006,128(4):753-760.(1) |
| [8] | Ehret P,Dowson D,Taylor C M.On lubricant transport conditions in elastohydrodynamic conjunctions[J].Proceedings of the Royal Society of London:Series A,1998,454:763-787.(1) |
| [9] | Johnson K J.Contact mechanics[M].Cambridge:Cambridge University Press,1985:53-56.(1) |
| [10] | Roelands C J A.Correlational aspects of the viscosity-temperature-pressure relationship of lubricanting oils[D].Delft:Delft University of Technology,1966.(1) |
| [11] | Dowson D,Higginson G R.Elastohydrodynamic lubrication,the fundamentals of roller and gear lubrication[M].Oxford:Pergamon Press,1966.(1) |
| [12] | Hu Y Z,Zhu D.A full numerical solution to the mixed lubrication in point contacts[J].Journal of Tribology,2000,122(1):1-9.(1) |
| [13] | Venner C H,ten Napel W E,Bosma R.Advanced multilevel solution of the EHL line contact problem[J].Journal of Tribology,1990,112(3):426-431.(1) |
| [14] | Patir N.A numerical procedure for random generation of rough surface[J].Wear,1978,47(2):263-277.(1) |