Corresponding author: JIANG Lian-yun, E-mail:neu2015@163.com.
热轧带钢在轧后一般采用普通层流冷却、加强型冷却和超快速冷却,这三种冷却方式冷却速率高低不同,但均是采用射流冲击的原理来实现[1, 2, 3].为了保证热轧带钢性能的稳定性,需要在轧后冷却系统中实现带钢温度的精准控制,而为了实现带钢温度的精准控制则需要准确的温度计算模型[4, 5].温度场计算模型可采用两种方法来获得:①根据热传导偏微分方程及其初始条件和边界条件可得到温度场计算模型,该计算方法考虑了带钢厚度方向温度梯度的存在;②忽略带钢厚度方向上的温度梯度,根据热流量守恒建立温度场微分方程,并由初始条件求解微分方程得到温度场计算模型,该计算方法称之为集总参数法.
方法①获得的温度场计算模型精度较高,但是该模型较为复杂,并且还需要求解超越方程,如果可能的话尽量不采用该计算模型;方法②获得的温度场模型较为简单,方便使用,在大多数轧后冷却生产线中得到了应用[6, 7, 8],但是由于对模型做了进一步的简化,需要对其适用范围进行分析,以进一步提高热轧带钢温度控制精度.
文献[9]指出了集总参数法的适用范围和条件,在同一时刻,采用方法①所计算的带钢心部、1/4和表面温度是不同的,而方法②所计算的各个位置的温度则是相同的,因此,在相同偏差范围内,在不同位置方法②的适用范围是不同的,采用统一的适用范围来表达集总参数法的适用范围是不恰当的.
在温度场模型实际应用中较关心带钢心部、1/4和表面[10],但是在轧后冷却控制系统中更关心带钢表面温度.经过分析与计算得到了相对偏差在5%和10%范围内,带钢不同位置集总参数法的适用范围和条件.在传热学中,毕渥数(Bi)是一个非常常见和重要的无量纲数,因此采用毕渥数表示集总参数法的适用范围.该研究将为热轧带钢温度计算模型的选择和温度控制精度的进一步提高提供理论参考.
1 模型的建立热轧带钢的厚度为1.0~20.0mm,宽度为1000~2000mm,长度大于100m,因此带钢的宽度和长度远大于其厚度.在温度场分析与计算时更关注厚度方向温度分布情况,此时带钢的传热问题可简化为一维非稳态传热问题.为了获得温度场的解析解需要对模型进行简化处理,下面是简化和假设的条件:
1) 带钢初始温度均匀,大小为t0;
2) 带钢的物性参数为常数且不随时间改变;
3) 介质温度为tf,且保持不变;
4) 带钢上下表面换热系数α相同,且不随时间变化.
由于带钢上下表面换热系数相同,温度分布沿厚度中心线对称,只需取其半模型进行研究,如图 1所示.
 | 图 1 热轧带钢温度场计算模型坐标系 Fig. 1 Temperature coordinates for hot rolled strip |
根据以上假设条件得到了一维非稳态传热问题的偏微分方程,并根据边界条件和初始条件得到了带钢温度场计算模型,如式(1)所示[11].

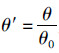 为无量纲过余温度;t,t0和tf分别为带钢温度、带钢初始温度和介质温度,℃;δ为带钢半厚,m;λ为导热系数,W/(m·K);ρ为密度,kg/m3;cp 为比热容,J/(kg·℃);α为换热系数,W/(m2·K);x为厚度方向位置,m;τ为冷却时间,s;a为带钢热扩散率;Bi为毕渥数,表征固体内部导热热阻与其界面上换热热阻之比的无量纲数;μn为式(2)第n个解.
为无量纲过余温度;t,t0和tf分别为带钢温度、带钢初始温度和介质温度,℃;δ为带钢半厚,m;λ为导热系数,W/(m·K);ρ为密度,kg/m3;cp 为比热容,J/(kg·℃);α为换热系数,W/(m2·K);x为厚度方向位置,m;τ为冷却时间,s;a为带钢热扩散率;Bi为毕渥数,表征固体内部导热热阻与其界面上换热热阻之比的无量纲数;μn为式(2)第n个解.
在式(1)中,由于级数的第二项后指数项的值非常小,采用级数的第一项与完整级数所计算的心部温度偏差在1%以内[11],因此,可取级数的第一项代替所有级数的和,并将 代入式(1)中可以得到温度场计算模型,如式(5)所示.
代入式(1)中可以得到温度场计算模型,如式(5)所示.

当带钢冷却过程中温度梯度较小时,可假定带钢温度均匀分布,忽略带钢厚度方向上的温度梯度,带钢温度只与冷却时间有关,因此该问题可简化为零维问题.根据热流量守恒可建立温度场微分方程,并由初始条件可以得到微分方程的解,该方程的解即为温度场计算模型[9],如式(6)所示.

由式(6)可以得到无量纲过余温度曲线,如图 2所示.令τ=ρcpδ/α,由式(6)可得θ/θ0=exp(-1)=0.368,这个指标一般用于表征物体对外界流体温度瞬间反应快慢的程度,它表示冷却过程已经进行到完全行程的63.2%所需的时间,称之为温度响应时间.在该时刻带钢的冷却过程已经完成,因此在误差分析时可取τ=ρcpδ/α.
 | 图 2 不同带钢厚度无量纲过余温度曲线 Fig. 2 Dimensionless excess temperature curves for various strip thicknesses |
由式(6)和图 2可知,可根据带钢温度计算冷却时间,也可以由冷却时间计算带钢温度.在带钢冷却过程中带钢温度将按照指数形式降低,在无限长时间后趋于平衡;在开始冷却阶段带钢温度下降较快,随着冷却过程的进行带钢温度变化趋于平缓,并将在无限长时间后到达稳定状态.
2 适用条件和计算偏差分析在工程实际应用中温度计算模型的相对偏差在5%以内是可接受的;在控制系统中,一般存在温度场计算模型自学习功能,模型计算相对偏差在10%以内时也能够通过模型自学习进行补偿,此时10%的计算误差也是可以接受的,具体的模型计算精度要求与所控制对象的控制精度高低有关,可根据控制精度需要选择计算模型.
令Bi=αδ/λ,F0=aτ/δ2,Bi=μ1tanμ1,则τ=ρcpδ/α=1/(BiF0),将其代入式(5)和式(6),并将两边相除进行整理可得

根据热轧带钢冷却工艺参数可知,带钢的毕渥数Bi < 2.0,根据Bi=μ1tanμ1可知此时μ1< 1.0,图 3为厚度方向不同位置处θ′/θ″曲线.
 | 图 3 厚度方向不同位置μ1- θ′/θ″ 曲线 Fig. 3 μ1-θ′/θ″ curves in different position along the thickness |
由图 3可以看出,随着μ1的增加相对偏差函数θ′/θ″也随之升高,即两者呈正比例关系,根据这个结论可以得到相对偏差小于5%和10%时毕渥数的取值范围.
x=0对应的带钢心部位置,将其代入式(7)中可以得到相对偏差为5%和10%时的不等式,如式(8)所示.

采用Matlab以及图 3的曲线可得到不等式(8a)的解为μ1< 0.3122,不等式(8b)的解为μ1< 0.4362;根据Bi=μ1tanμ1可得,当带钢心部计算值相对偏差在5%以内时Bi< 0.1008,带钢心部计算值相对偏差在10%以内时Bi< 0.2033.
x=δ/2对应带钢1/4位置处,将其代入式(7)中可以得到相对偏差为5%和10%时的不等式,如式(9)所示.

采用Matlab以及图 3的曲线可得到不等式(9a)的解为μ1< 0.3608,不等式(9b)的解为μ1<0.5042;根据Bi=μ1tanμ1可得,当带钢1/4位置处计算值相对偏差在5%以内时Bi< 0.1361,带钢1/4位置处计算值相对偏差在10%以内时Bi<0.2782.
x=δ对应带钢表面位置,将其代入式(7)中可以得到相对偏差为5%和10%时的不等式,如式(10)所示.

采用Matlab以及图 3的曲线可得到不等式(10a)的解为μ1< 0.8473,不等式(10b)的解为μ1< 0.9877,根据Bi=μ1tanμ1可得,当带钢表面计算值相对偏差在5%以内时Bi< 0.9593,带钢表面计算值相对偏差在10%以内时Bi< 1.4974.
对以上计算和分析结果进行整理可以得到带钢不同位置采用集总参数法所计算结果偏差为5%和10%时的毕渥数范围,如表 1所示.
| 表 1 不同位置和偏差范围时Bi取值范围 Table 1 Range of Biot with different position and deviation range |
由表 1中的计算结果可以看出,在相同的偏差范围内,带钢心部的Bi取值范围最小,带钢 1/4位置处次之,带钢表面最大,由此可知采用集总参数法所得到的温度场计算模型表面温度计算精度最高,1/4位置次之,心部温度计算精度最低,即越靠近带钢表面温度计算精度越高.
在采用集总参数法计算带钢温度场模型时忽略厚度方向上的温度梯度,而带钢表面按照热对流进行处理,正好与实际冷却过程相符合,因此,带钢表面温度计算精度最高.在热轧带钢生产线只能测量带钢表面温度,在带钢温度控制时一般只对带钢表面温度进行控制,采用集总参数法所得到的计算模型适用范围进一步扩大.
热轧带钢在轧后及冷却后的温度一般为300~900℃,在该范围内带钢的导热系数在27~50J/(kg·℃),层流冷却平均换热系数在500~2000W/(m2·K),带钢厚度为2.0~25.0mm,根据Bi=2αδ/λ,可以得到层流冷却时Bi的范围为0.01~0.93.在热轧带钢轧后冷却系统主要对带钢表面温度进行控制,而集总参数法计算的表面温度相对偏差在5%以内时Bi值范围为0~0.9593,因此,在层流冷却模式下可采用集总参数法所得到的温度计算模型.
轧后超快速冷却换热系数明显高于层流冷却换热系数,Bi值较大,需要根据实际的Bi值大小选择温度计算模型,具体如下:
1) Bi< 0.96(具体大小依温度计算精度要求而定)时,采用集总参数法所得到的温度计算模型;
2) Bi ≥0.96时,采用一般解法所得到的温度计算模型.
3 结论1) 集总参数法所得到的温度计算模型可用于带钢温度计算,在不同位置处,集总参数法所计算精度有所区别,带钢表面温度计算精度最高,1/4次之,心部最低,即距离带钢表面距离越近,计算精度越高.
2) 集总参数法所得到的温度场计算模型,计算相对偏差在5%以内时,带钢心部、1/4和表面毕渥数范围分别为0~0.1008,0~0.1361和0~0.9593;计算相对偏差在10%以内时,带钢心部、1/4和表面毕渥数范围分别为0~0.2033,0~0.2782和0~1.4974.
| [1] | Sharif M A R.Heat transfer from an isothermally heated flat surface due to twin oblique slot-jet impingement[J]. Procedia Engineering, 2013, 56(5):544-550.( 1) 1) |
| [2] | Jeng T M, Tzeng S C, Xu R.Heat transfer characteristics of a rotating cylinder with a lateral air impinging jet[J]. International Journal of Heat and Mass Transfer, 2014, 70(6):235-249.( 1) 1) |
| [3] | Wang B X, Xie Q, Wang Z D, et al.Fluid flow characteristics of single inclined circular jet impingement for ultra-fast cooling[J]. Journal of Central South University, 2013, 20(11):2960-2966.( 1) 1) |
| [4] | Wang J, Wang G D, Liu X H.Hot strip laminar cooling control model[J]. Journal of Iron and Steel Research, International, 2004, 11(5):13-17.( 1) 1) |
| [5] | Park C T, Yoon K S, Lee C H.Advanced temperature control of high carbon steel for hot strip mills[J]. Journal of Mechanical Science and Technology, 2010, 24(5):1011-1017.( 1) 1) |
| [6] | Liu E Y, Peng L G, Yuan G, et al.Advanced run-out table cooling technology based on ultra fast cooling and laminar cooling in hot strip mill[J]. Journal of Central South University of Technology, 2012, 19(5):1341-1345.( 1) 1) |
| [7] | Li H J, Li Z L, Yuan G, et al.Development of new generation cooling control system after rolling in hot rolled strip based on UFC[J]. Journal of Iron and Steel Research, International, 2013, 20(7):29-34.( 1) 1) |
| [8] | 李振垒, 李海军, 王昭东, 等.热轧板带钢的超快速冷却控制系统[J]. 东北大学学报:自然科学版, 2012, 33(12):1436-1439. (Li Zhen-lei, Li Hai-jun, Wang Zhao-dong, et al.Ultra-fast cooling control system for hot rolling strip[J]. Journal of Northeastern University :Natural Science, 2012, 33(12):1436-1439.)( 1) 1) |
| [9] | S 赵镇南.传热学[M]. 北京:高等教育出版社, 2002:123-126. (Zhao Zhen-nan.Heat transfer[M]. Beijing:Higher Education Press, 2002:123-126.)( 2) 2) |
| [10] | Yuan G, Li Z L, Li H J, et al.Control and application of cooling path after rolling for hot strip based on ultra fast cooling[J]. Journal of Central South University, 2013, 20(7):1805-1811.( 1) 1) |
| [11] | 于明.中厚板轧后冷却过程温度场解析解研究与应用[D]. 沈阳:东北大学, 2008. (Yu Ming.Research and application of analytical solution for temperature field in accelerated cooling process of plate[D]. Shenyang:Northeastern University, 2008.)( 2) 2) |




