Corresponding author: YAO Hong-liang, E-mail: hlyao@mail.neu.edu.cn
旋转机械碰摩故障的动力学形式很多,如周期、拟周期、混沌等,对其动态特性进行数值仿真很重要.目前对旋转机械动力学分析采用的主要方法有时域和频域两种.时域方法包括初值积分方法:Runge-Kutta方法[1]、Newmark-β方法等[2].
在分析相同振动问题时,频域分析方法的速度要比时域分析方法快很多,同时,该方法还能够直接揭示出系统中频率的各种特性.目前,常用的频域分析方法主要包括谐波平衡法(harmonic balance,HB)[3]、描述函数法(describing function,DF)[4]、增量谐波平衡法(incremental harmonic balance,IHB)等.
增量谐波平衡法,由Lau和Cheung等最早提出[5],该方法不仅可以分析弱非线性问题,还能分析强非线性问题,并能灵活控制算法的收敛精度,是研究强非线性问题稳态周期响应的有效方法.采用该方法能够分析非线性振动的周期响应、拟周期响应、周期解稳定性等问题,目前已经在转子动力学响应分析等方面得到了广泛的应用[6, 7].
现代大型旋转机械往往具有多跨转子结构.但是由于多跨转子系统结构复杂,动力学建模后自由度很多,如果直接采用增量谐波平衡法进行响应分析,势必遇到耗时长等问题.为了利用其稳态振动求解的优势并同时克服多自由度时计算效率低的问题,本文针对多跨碰摩故障转子系统的局部非线性特点,将固定界面模态综合法与增量谐波平衡法相结合,提出了一种新的降维增量谐波平衡法,并利用某双跨转子系统的仿真验证了该方法的有效性和效率.
1 碰摩转子模型建立方法设转子系统由弹性轴段单元组成,如图 1所示.轴段单元的广义坐标为两端节点的位移,仅考虑弯曲变形和扭转变形,而忽略轴向变形,则每个轴段的广义坐标为

 | 图 1 轴段有限元模型 Fig. 1 The finite element model of the shaft segment |
采用有限元建模方法,碰摩转子系统的运动微分方程为

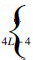 ,则碰摩力向量可以表示为Fb0=[0,…,0,Px,Py,0,…,0]T,Px,Py为碰摩力在x和y方向的分量.碰摩力的具体表达式为
,则碰摩力向量可以表示为Fb0=[0,…,0,Px,Py,0,…,0]T,Px,Py为碰摩力在x和y方向的分量.碰摩力的具体表达式为

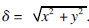 .
2 固定界面模态综合法降维
.
2 固定界面模态综合法降维
对于多跨转子系统,由于每个节点有4个自由度,所以当划分的转子系统具有几十甚至上百个节点时,所建立动力学模型的自由度将达到上百个甚至上千个.
为了提高计算效率,可以采用固定界面模态综合法(component mode synthesis,CMS)进行自由度的降维[8].将式(2)重新划分为线性和非线性(即碰摩位置)两部分,如式(4)所示,


假设给某个界面自由度单位位移,保持其他界面自由度为0,形成该自由度下的约束模态,

对每个界面自由度按式(6)操作,形成约束模态集ψc,

由固定主模态集和约束模态集组合可得系统的模态矩阵ψ:

因此,将式(4)变换为模态坐标下的振动方程为

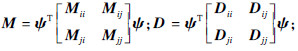
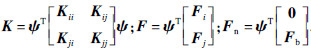 .
.
采用数值方法求得方程(9)在模态坐标下的解u,利用x=ψu返回到原物理坐标,可得原系统的动态响应.
可见系统的降维主要依靠主模态集的缩减实现,主模态集中模态数越小,所得模型的自由度越少,但是可能会影响所求得响应的精度.
3 降维后系统的增量谐波平衡求解法对降维后的系统采用增量谐波平衡法求解.
取τ=ωt,则方程(9)转化为

当系统存在稳态响应时,假设取到第r次谐波,则第i个自由度的响应为

取S=diag[Cs Cs … Cs],A=[A1T A2T … AhT]T,则u=SA.
设


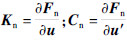 .
.
对式(13)取Galerkin过程并整理,有

即

对式(15)进行迭代,可以求得A0,从而求得u.
4 弧长法弧长法是Newton-Raphson迭代方法的一种改进迭代方法[9],与增量谐波平衡法相结合能够求得系统的不稳定稳态解.
针对式(15),取


增加控制方程

联立式(17)和式(18)求解ΔA和Δλ,由 A=A(i+1)=A(i)+ΔA,λ=λ(i+1)=λ(i)+Δλ,ω=ω(i+1)=λω(i)迭代求出最终解.
5 仿真与讨论某双跨转子系统如图 2所示,左侧为高压缸,右侧为低压缸,划分单元尺寸详见表 1.双跨转子之间用膜片联轴器相连,由于膜片联轴器刚度较低,故针对实际结构采用外径160 mm,内径140 mm,长500 mm的空心轴段来代替.此轴段介于表 1中15轴段和16轴段之间,即16和17节点间.
 | 图 2 双跨转子系统模型 Fig. 2 Model of the two span rotor system |
| 表 1 双跨转子系统轴段尺寸 Table 1 Shaft segment dimension of the two span rotor system |
取转子系统弹性模量为2.1×1011 Pa,高压缸偏心位于节点8,9处,偏心大小为mr1= 5×10-3 kg·m,两点的相位同时为0;低压缸偏心位于节点24,25处,偏心大小为mr2= 4×10-2 kg·m.高压缸支撑刚度为1.5×108 N/m,低压缸支撑刚度为1×109 N/m.系统阻尼为比例阻尼,其中α=0,β=0.000 5.假设碰摩发生在第24节点处,碰摩形式为整周碰摩.
设碰摩间隙为1×104 m,碰摩刚度为2×108 N/m,摩擦系数为0.15,求得碰摩点(低压缸上24节点)和非碰摩点(高压缸上8节点) x方向的幅频响应曲线分别如图 3a和3b所示.图中对比了不采用降维和采用CMS降维方法的精度,以不降维的结果为标准值,Z为采用CMS方法时所取的主模态数目.从图中可以看出,当主模态数目较小时(Z=5),计算结果与标准值的偏差较大,当Z=10时计算结果已经非常接近标准值,这说明本文方法的精度可以满足要求.
 | 图 3 小碰摩刚度时的幅频响应曲线 Fig. 3 Amplitude-frequency response curves with small rubbing stiffness (a)—碰摩点;(b)—非碰摩点. |
设其他参数不变,将碰摩刚度增至109 N/m,求得24节点和8节点x方向的幅频响应曲线分别如图 4a和4b所示.可见在碰摩刚度较大时,采用CMS方法进行降维后,仍然能够得到与标准值相近的结果.同时可以看出,在大碰摩刚度下,幅频响应曲线中存在不稳定区,不稳定解的求解是采用IHB方法结合弧长法的一个突出优点.
 | 图 4 大碰摩刚度时的幅频响应曲线 Fig. 4 Amplitude-frequency response curves with large rubbing stiffness (a)—碰摩点;(b)—非碰摩点. |
接下来通过对比计算某一固定转速下的稳态响应时所需的时间来说明本文方法的效率.所采用计算机性能:CPU2.83 GB,内存3.25 GB,采用编程语言MATLAB,每个周期积分取200步,计算所需时间结果见表 2.
| 表 2 运行所需CPU时间对比 Table 2 Comparison of CPU time |
由以上分析可见,降维后所用时间相比于未降维时明显减少.在主模态数取Z=10时,计算结果已经与不降维方法基本一致,而所用时间仅为不降维方法的1/25,验证了该方法的有效性.
6 结 论1) 结合固定界面模态综合法和增量谐波平衡法提出了降维增量谐波平衡方法,可以通过调整主模态数控制响应计算所需的时间.
2) 双跨转子系统的仿真表明主模态数取10时精度已经满足要求,而消耗时间缩短为1/25,证明了该方法具有较高的精度和效率.
| [1] | Meybodi R R,Mohammadi A K,Bakhtiari-Nejad F.Numerical analysis of a rigid rotor supported by aerodynamic four-lobe journal bearing system with mass unbalance[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(1):454-471.( 1) 1) |
| [2] | Bouaziz S,Belhadj M N,Choley J,et al.Transient response of a rotor-AMBs system connected by a flexible mechanical coupling[J].Mechatronics,2013,23(6):573-580.( 1) 1) |
| [3] | Wang C.Application of a hybrid method to the nonlinear dynamic analysis of a flexible rotor supported by a spherical gas-lubricated bearing system[J].Nonlinear Analysis:Theory,Methods & Applications,2009,70(5):2035-2053.( 1) 1) |
| [4] | Wei F,Zheng G T.Multiharmonic response analysis of systems with local nonlinearities based on describing functions and linear receptance[J].Journal of Vibration and Acoustics,2010,132(3):0310041- 0310046.( 1) 1) |
| [5] | Lau S L,Cheung Y K,Wu S Y.Incremental harmonic balance method with multiple time scales for nonlinear aperiodic vibrations[J].ASME Journal of Applied Mechanics,1983,50(1):871-876.( 1) 1) |
| [6] | Shen Y J,Yang S P,Liu X D.Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method[J].International Journal of Mechanical Sciences,2006,48(11):1256-1263.( 1) 1) |
| [7] | 姚红良,许琦,茅列前,等.行星齿轮系统弯扭耦合振动的增量谐波平衡求解方法[J].东北大学学报:自然科学版,2013,34(8):1451-1456.(Yao Hong-liang,Xu Qi,Mao Lie-qian,et al.Incremental harmonic balance method for coupled bending and torsional vibration in planetary gear system[J].Journal of Northeastern University:Natural Science,2013,34(8):1451-1456.)( 1) 1) |
| [8] | Kawamura S,Naito T,Zahid H M,et al.Analysis of nonlinear steady state vibration of a multi-degree-of-freedom system using component mode synthesis method[J].Applied Acoustics,2008,69(7):624-633.( 1) 1) |
| [9] | Ferreira J V,Serpa A L.Application of the arc-length method in nonlinear frequency response[J].Journal of Sound and Vibration,2005,284(1):133-149.( 1) 1) |




