急倾斜破碎中厚矿体是冶金矿山的难采矿体之一，通常应用有底柱崩落法或阶段矿房法开采；由于采准工程难以形成或形成后塌冒严重等原因，采场事故率高，矿石损失、贫化大.近年来，一些矿山试用诱导冒落法开采^[1]，在阶段的下部只布置一条沿脉进路，按步距爆破回采一定的高度，形成一定跨度的采空区，诱导上部矿岩自然冒落，冒落的矿石从回采进路的端部出矿口放出，冒落的废石留在采场形成覆盖层.这种采矿方法的主要优点是：减小常规底部结构对矿岩的切割程度，降低采动压力破坏，有效解决了采切工程难以形成或形成后塌冒严重的难题，改善了采场安全生产条件.此外，采场上部的大部分矿体诱导冒落，采准系数小，开采效率高，因此，对于难以开采的急倾斜破碎中厚矿体而言，沿脉进路诱导冒落法不失为一种有发展前景的高效采矿方法；但这种采矿方法在生产中存在着回采指标(贫化率、回收率)不稳定的问题，当沿脉回采进路的位置选择不当时，往往造成较大的矿石损失与贫化.为此，需要根据沿脉进路诱导崩落法落矿与放矿工艺特点，以矿石回收率和贫化率为指标，研究不同倾角条件下沿脉进路位置的确定方法.

1.1 最佳进路位置选定的理论依据

急倾斜破碎中厚矿体诱导冒落法的采场结构如图1所示，利用爆破后放矿形成的诱导空间，诱导其上部矿岩自然冒落^[2].在此过程中，沿脉进路一是用于崩落区的凿岩与爆破，将诱导冒落区的下部矿岩崩落；二是用于出矿，将崩落与冒落的矿石放出.沿脉进路的位置不同，出矿时引起的散体移动范围不同，而只有处于散体移动范围之内的崩落与冒落矿岩，才能在进路出矿过程中发生下移或被放出，那些发生移动的部位，才能为采场上部矿石的冒落提供碎胀空间^{[3, 4]}.而被放出的矿石，仅仅为进入放出体之内的矿石，位于放出体之外的移动矿石，变成迁移残留，残留于矿体的下盘^{[5, 6, 7]}.沿脉进路的位置，既决定了散体发生移动的范围，又决定了放出体的位置，因此，它不但影响上部矿石诱导冒落的范围，而且影响崩落与冒落矿石的放出量，是影响矿石回收指标的根本原因.

当沿脉进路处于最佳位置时，崩落区爆破出矿后形成的空区，能够诱导上部矿石自然冒落的范围达到最大值，同时，从端部出矿口放出的矿石量应能达到矿石回采指标最佳的要求.分析得出，在急倾斜破碎中厚矿体条件下，满足后一条件的进路位置，一般也能满足前一条件.为此.在实验研究不同倾角条件下的沿脉进路最佳位置确定方法时，可将问题简化为，寻求第一倾角条件下矿石回采指标最佳的沿脉进路位置.

图1所示方案中，正常回采时，崩落与冒落的矿石均在覆岩下放出，当放出体深入到覆岩中时，废石掺杂矿石一起放出；增加放出量，可提高矿石的回收率，但矿石的贫化率也将随之增大，此时，矿石回收率与贫化率成为矛盾统一体.本次物理模拟实验中采用了常用的截止品位放矿方式，即每个步距在当次放矿量达到截止品位时停止放矿.

图 1(Figure 1)

Fig. 1

1—沿脉回采进路;2—出矿横穿;3—出矿联巷;4—落矿炮孔;5—预测冒落线;6—覆岩;7—上分段残留矿体;8—炮孔推进方向;9—切割巷道;10—矿体界线;α—矿体倾角;H—阶段高度;h—崩落高度;L—采场长度;B—崩落区;A—诱导冒落区.图 1 沿脉进路诱导冒落法开采方案图 Fig. 1 Mining scheme of induced caving method of the following-vein drift

沿脉进路处于不同位置时所得矿石回收率和贫化率指标不尽相同.比较两种方案的回收率、贫化率指标，有以下4种情况：①矿石回收率相同，贫化率不同；②矿石贫化率相同，回收率不同；③矿石的回收率与贫化率均不相同，但其中一个方案的回收率高、贫化率低；④矿石的回收率与贫化率均不相同，但回收率高的贫化率也高，回收率低的贫化率也低.本文采用综合评定的比较方法：首先，通过数量指标进行比较，该方法较直观.比较原则：矿石回收率相同，贫化率不同，贫化率低者为优；矿石贫化率相同，回收率不同，且贫化率相对较小，以矿石回收率高者为优；矿石回收率、贫化率均不同，以矿石回收率高、贫化率低的一组为优.其次，在数量指标难以比较时，可通过经济指标进行比较，即根据式(1)进行比较^{[8, 9, 10]}.

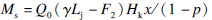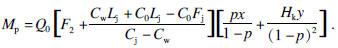
M₀为总盈利额，正值为盈利，负值为亏损，元；M_s为工业矿石量改变所代表的经济价值，元；M_p为混入岩石量改变所代表的经济价值，元；Q₀为崩落工业矿量，t；γ为精矿产出率，%；L_j为精矿售价，元/t；F₂为每吨矿石从放矿到选矿的费用，元/t；H_k为工业矿石回收率，%；p为贫化率，%；x为回收率的改变量，%；y为贫化率的改变量，%；C_w为尾矿品位，%；C_j为精矿品位，%；C₀为工业矿石品位，%；F_j为精矿成本，元/t.

由于Q₀为M_s，M_p共同的因子，不影响比较效果，因此，可以省略，此外，某一时期，某一企业，部分参数为固定值，因此可将M_s，M_p简化为

式中K₁和K₂皆为大于1的系数，该参数与不同时期矿山企业技术经济指标有关.

实验中，不同进路回收率、贫化率引起的经济指标比较转化为值M′₀ 的比较，即M′₀大的进路为最佳进路.

以双鸭山铁矿北区矿体条件、采场结构参数 为原型进行物理模拟实验，原型条件为：矿体倾角70°~90°，平均水平厚度10 m，矿体沿走向长度取18 m，阶段高度50 m，崩矿步距2.2~2.5 m.进路断面尺寸为2.8 m×2.8 m，模型几何相似比1∶100，物理模型如图2所示.回采进路沿矿体走向布置，从矿体中心位置向下盘方向移动，移动范围0~3.6 cm，由进路活动板控制.调整矿体倾角控制板可改变矿体倾角.受爆破挤压作用及矿石碎胀性等因素影响，崩落后的矿石层厚度比崩矿步距大15%~20%^[10]，因此，本实验放矿步距取3 cm.共设7个步距，第1步距装填废石，之后6个步距装填矿石，覆岩厚度保持20 cm，矿石、覆岩颗粒级配见表1.

图 2(Figure 2)

Fig. 2

图 2 模型装入矿石、白云岩后的正、侧面图 Fig. 2 Front and side views of model loaded in ore and dolomite

表 1

Table 1

表 1(Table 1)

表 1 散体的颗粒级配 Table 1 Particle gradation of loosening body 散体类别 实验散体力度级配/% 散体容重 < 1.25 mm 1.25~2.5 mm 2.5~5 mm 5~6 mm 6~7 mm 7~8 mm g·cm-3 磁铁矿石 20.6 21.1 27.8 24.8 3.7 2.0 2.41 白云岩 2.3 26.3 55.8 13.4 1.5 0.7 1.62

表 1 散体的颗粒级配 Table 1 Particle gradation of loosening body

2.1 残留体形态实验

模拟的矿体倾角从90°向70°逐次变化，每5°为一单元.矿体倾角70°~90°时，角度变动一次，进路位置(进路中心线距矿体下盘的距离)分别为5，4.3，3.6，3.1，2.6，2.1和1.4 cm.每次放出矿岩质量为128~144 g，单次放出量达到矿石与岩石体积比为1∶1时，即接近截止品位，停止该步距放矿，转入下一步距放矿，直至最后一个步距放矿结束.根据实验所得回收率和贫化率指标能够确定最佳的进路位置.该实验目的主要是确定首分段回采进路最佳位置随倾角变化的趋势，并得到残留体量及残留体形态，为第二分段放矿得到完整回采指标做准备.

将处于最佳回采进路位置时的残留体布置在上分段，其余部位矿岩装填方式不变.矿体倾角变化及放矿过程与残留体形态实验相同，不同的是：矿体倾角70°~90°时，角度变动一次，进路位置变动的主要位置为5，3.6，2.6和1.4 cm.

3.1 进路最佳位置与矿体倾角的关系

定义R为最佳进路位置至下盘距离与矿体厚度的比值，R值表征了进路在矿体中的相对位置；R值越小，进路位置越靠近下盘.通过残留体形态实验的矿石回收情况，得出R值随倾角α 变化的趋势(见图3).从图中可以看出：伴随矿体倾角α的减小，R以曲线形式逐渐变小.矿体倾角在90°~85°，70°~80°时，R值变化较小;85°~80°之间，R值受倾角影响较大，该范围内R值的小幅度变化都会对回收率、贫化率造成较大影响，说明该范围内，散体受重力场作用及边壁条件影响较大，崩落与冒落的矿石移动范围受倾角影响明显.

图 3(Figure 3)

Fig. 3

图 3 R值随倾角变化关系 Fig. 3 Relationship between the ratio R and orebody dip angle α

诱导冒落法回采指标实验得到的矿石回收率、贫化率见表2.由表2可看出：矿体倾角不同，R值对回收率、贫化率的影响程度不同.通过最佳进路位置的选择，得到不同倾角下的最佳位置所对应的R值.以矿体倾角90°为例：用数量指标的方法，R值为0.26，0.14时与R值为0.5，0.36时相比，回收率小而贫化率大，由此判断R值为0.26，0.14时的进路位置不合理；R值为0.5和0.36时两组数量指标相差较小，因此，需要通过经济指标进行比较.本文以2013年铁矿实际的经济指标计算，C₀=28.83%，C_j=66%，C_w=6%，γ=38.33%，，L_j=880元/t，F₂=73元/t，F_j=580元/t，K₁=264.3，K₂=305.2，x=0.94%，y=0.47%；代入式(2)得到M₀′=0.025.说明R值为0.5时的进路位置最佳.同理可得到其余角度最佳进路位置如下：倾角85°时，R值为0.5；倾角80°时，R值为0.26；倾角75°时，R值为0.14；从倾角大于75°时最佳进路位置对应的回采指标看，回收率皆大于81%，贫化率不足19.5%，能够得到较好的回采指标.而当倾角为70°时，即便回采进路紧靠下盘，回收率也不足76%，下盘残留量过大，因此，在矿体倾角小于75°时，不适合采用阶段诱导冒落法.

表 2

Table 2

表 2(Table 2)

表 2 矿石回收率、贫化率 Table 2 Ore recovery and dilution ratio α/(°) R=0.5 R=0.36 R=0.26 R=0.14 Hk p Hk p Hk p Hk p 90 82.39 19.48 81.45 19.01 77.60 19.54 75.81 20.31 85 81.95 18.73 81.50 18.95 78.57 19.20 75.33 19.00 80 76.69 18.79 80.55 19.01 81.29 18.54 77.83 17.23 75 73.64 19.83 77.28 20.25 74.67 16.66 81.18 17.53 70 60.76 21.79 64.70 21.16 66.87 20.20 75.84 19.91

表 2 矿石回收率、贫化率 Table 2 Ore recovery and dilution ratio

从物理实验数据中可看出：进路位置对矿体回收的影响非常重要.因此，在确保回收率的情况下，需结合施工条件、开凿效果等因素，设置沿脉进路的位置，使冒落能够有序进行，废石混入冒落矿石堆体较少.在实验条件下(矿体倾角75°~90°，平均厚度10 m)，当矿体倾角大于85°时，最佳的进路位置为进路中心线距离矿体下盘约5 m处；当矿体倾角80°~85°时，进路中心线应选在距离矿体下盘约2.5 m处；当矿体倾角在75°~80°时，将进路中心线紧贴下盘布置最佳.

1) 在应用诱导冒落法回采急倾斜破碎中厚矿体时，回采进路位置对诱导冒落区的矿体冒落和放出体发育影响重大，是影响矿石损失贫化的关键因素.

2) 将物理实验得到的回收率、贫化率数量指标与经济指标相结合，给出了一种最佳进路位置确定的综合评判方法.用该方法确定了不同倾角下的最佳进路位置.R值随倾角的减小变小；当倾角小于75°时，不适合采用阶段诱导冒落法方案.

3) 根据实验结果，给出了10 m左右厚度的中厚矿体在段高50 m、倾角为75°~90°区间内的最佳进路位置.研究结果对具有类似矿体条件的矿山具有一定的参考价值.