2012年沈阳市固定资产投资额为5625.4亿元,其中,房地产开发投资额为1942.96亿元,占固定资产投资额的34.54%.由此可见,沈阳市房地产市场建设情况影响着城市发展和人民生活水平.密切关注房地产市场、保证房地产市场平稳运行是保证人民生活水平和城市发展的重要内容[1].目前常用的反映房地产市场情况的指标是房地产价格指数,国内外房地产价格指数有很多,适用条件和计算方法也不尽相同,如何选择正确的、合适的方法计算房地产价格指数是进行房地产市场管理的首要问题[2].
1 房地产价格指数及编制方法1.1 国内外房地产价格指数
美国住宅价格指数(HPI),由美国联邦住宅供给机构监察办公室负责采用重复销售法进行编制,主要反映住宅价格的变动情况.主要数据包括:美国50个州与华盛顿特区的房价评估及排名;美国九大地区房价百分比变化;对220个大都市的房价评估排名.
加拿大综合房屋价格指数,由Teranet公司和加拿大国民银行采用重复销售法进行编制,主要反映公寓、城镇房屋和住宅销售价格情况.主要数据包括:温哥华、卡尔加里、多伦多、渥太华、蒙特利尔和哈利法克斯区域指数;6个指数赋予不同权重形成一个国家综合指数.
英国住宅价格指数(Halifax HPI),由英国房屋抵押贷款协会采用特征价格法进行编制,主要反映抵押住房情况.主要数据包括:综合价格指数,独栋、联体、叠拼、公寓指数,首次购房者指数,国资购房者指数,新、半新、旧房屋指数.
中房指数,由中国指数研究院采用加权综合指数法和特征价格法进行编制.主要反映预售项目、新建商品住宅及二手房价格.主要数据包括:十个城市提供综合指数、住宅指数、Hedonic指数、商铺指数、写字楼指数,其中北京、上海、广州、深圳同时还提供二手房指数、别墅指数、普通住宅租赁价格指数.
全国70个大中城市房地产价格指数由国家统计局采用固定权数加权平均法进行编制.主要反映销售项目、租赁项目及土地价格.主要数据包括:土地出让价格指数、房屋销售价格指数、房屋租赁价格指数和物业服务价格分类价格指数.
伟业指数,由伟业顾问与清华大学房地产研究所采用特征价格法进行编制.主要反映销售项目及租赁项目(写字楼)价格.主要数据包括:北京市普通住宅、公寓、别墅、写字楼的价格和租金指数.
1.2 房地产价格指数编制方法房地产价格指数的编制方法有很多,但归纳起来主要有两大类:第一类是直接应用价格指数理论,另一类是应用特征价格理论[3].
直接应用价格指数理论常用的方法包括:加权平均法、成本投入法和中位数价格法.这几种方法简便易行,无需大量样本,适用于计算综合房地产价格指数.
应用特征价格理论常用的方法包括:特征价格法、重复交易法和混合模型法.特征价格法取样容易,可以得到大量价格资料,计算相对简单,但存在多重共线性问题和因房地产的个别性而掩盖市场供求关系对价格影响的问题;重复交易法是基于同一宗房地产价格变化运行的,如果剔除折旧的影响,就可满足房地产价格同质性的需要,但合适的样本数量非常有限,误差较大;混合模型法是综合特征价格法和重复交易法的一种改进方法,数据资料比较容易获得,样本误差也比较小,但仍然存在多重共线性问题[4, 5].
1.3 沈阳市商品住宅价格指数编制方法选择沈阳市各区域、各类型房地产都有着不同特点,综合房地产价格指数并不能全面反映沈阳市房地产市场的真实情况,只能进行宏观趋势的预测.本文选取沈阳市的商品住宅作为研究对象,旨在分析影响商品住宅的市场因素.直接应用价格指数理论计算沈阳市房地产价格指数不是非常合适,能满足重复交易法的计算价格指数的样本又极其有限,因此,本文采用特征价格法进行沈阳市商品住宅价格指数的编制.
2 沈阳市商品住宅特征价格建模2.1 特征变量的选择
影响商品住宅价格的因素很多,但特征价格法对变量的要求是避免多重共线性,这就要求在选择特征变量时,应尽可能选择影响力较大的因素[6].为了分析方便,将特征变量分为建筑特征、邻里特征和区位特征.建筑特征指住宅本身的情况,包括:建筑面积、房间数目、建筑朝向、装修程度[7]、有无车库、建筑质量.邻里特征指住宅小区的情况,包括:容积率、小区环境、物业管理、文体设施、基础设施配套、噪声[8, 9].区位特征指住宅小区周边情况,包括:至CBD(central business district)距离、至地铁口距离、至医院距离、公共交通.
2.2 特征价格模型的构建特征价格模型函数常用的有三种:基本模型、对数模型和半对数模型.本文采用半对数模型lnP=α0+∑αiCi+ε构建沈阳市商品住宅特征价格模型.
选择沈阳市商品住宅价格(P)作为因变量,建筑特征向量(S)、邻里特征向量(N)和区位特征向量(L) 作为自变量,其基本函数模型为
模型的估计方法采用最小二乘法(OLS),即

通过求偏导数,可以得出商品住宅特征的隐含价格及特征价格.
评价模型的好坏有两个标准:一是拟合优度,实践中采用校正的判定系数R来度量拟合度,R越高,则模型越好;二是理论一致性,模型中向量符号与实际情况相悖,即使拟合度再高也不能说模型合理,只有模型计算结果与理论解释具有很好的一致性,才证明模型是合适的.
2.3 特征价格模型的检验对2014年1月至2014年4月沈阳市研究区域内(市内五区)146个住宅小区进行调研,住宅小区的选择兼顾建筑特征、邻里特征和区位特征,保证每种特征小区数量基本相当,对挂牌价格进行修正,得到有效样本数量146个.运用统计软件SPSS对样本进行回归分析,在5%显著性水平下从模型的方差分析可以看出:采用半对数模型求得的复相关系数为83.6%,大于基本模型计算得出的复相关系数80%,这证明了半对数模型的选择更适合沈阳市商品住宅特征价格的计算.半对数模型的判定系数R2=69.9%,经调整的R2=66.1%,说明因变量和自变量之间线性关系明显,模型对因变量差异的解释能力约为66.1%.从回归分析来看:显著性检验值为0.000,说明房屋价格与其特征呈现密切的线性相关,见表 1.
| 表 1 模型回归分析表 Table 1 Model regression analysis |
从散点图(图 1)可以看出:无论是回归标准化残差还是回归标准化预计值,绝大多数点都分 布在-2至+2之间,只有9个点不在此范围内,满足方差齐性假设.从回归标准化残差的标准P-P图(图 2)可以看出:半对数模型的曲线近似于直线,可见残差符合正态分布.半对数模型不仅
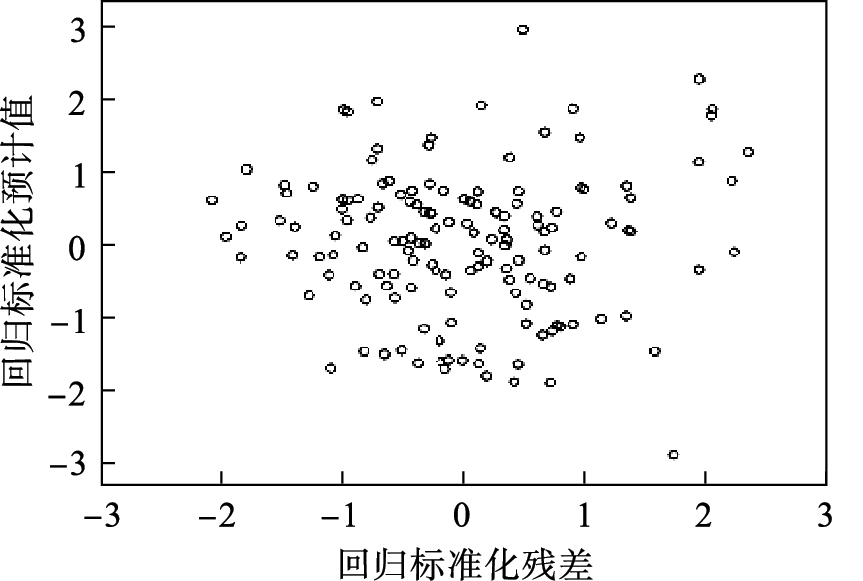 | 图 1 残差散点图 Fig. 1 Scatter diagram of residuals |
 | 图 2 回归标准化残差的标准P-P图 Fig. 2 Standard P-P diagram of regression standardized residuals |
满足正态性假设和等方差性假设,而且具有很好的拟合度和较高的解释能力,用来分析和解释商品住宅特征对商品住宅价格的影响是比较合适的.
2.4 特征价格分析通过半对数模型的分析,并与理论一致性相比较,去除建筑朝向、文体设施两项与理论相悖的因素,得出沈阳市商品住宅特征价格模型:
lnP=8.666+0.004×建筑面积+0.055×有无车库+0.138×装修程度-
0.129×房间数目+0.017×
建筑质量+0.001×小区环境+
0.048×物业管理+0.021×
容积率+0.003×基础设施配套+
0.014×噪声-0.027×
至CBD距离-0.008×
至地铁口距离+0.012×
至医院距离+0.013×公共交通.
由模型可知:其他变量不发生变化时,建筑面积每增加1m2,商品住宅单价将增加e0.004=1元.同理,可计算得出其他特征价格对商品住宅价格的影响.
3 沈阳市商品住宅特征价格指数设计与分析3.1 沈阳市商品住宅特征价格指数设计
采用商品住宅特征价格模型,以2005年1月沈阳市商品住宅特征价格为基期水平,商品住宅特征价格指数为

计算2006年至2013年沈阳市商品住宅特征价格指数,结果见表 2.
| 表 2 2006年至2013年沈阳市商品住宅特征价格指数 Table 2 Hedonic price index of Shenyang commercial housing from 2006 to 2013 |
从2006年至2013年沈阳市商品住宅特征价格指数来看,沈阳市商品住宅市场始终保持稳步上升态势.从指数增长率来看,2007年至2010年成上涨态势,2011年至2013年指数增长率有所减缓,总体趋势符合正态分布.沈阳市2007年至2013年商品住宅特征价格指数增长率趋势图如图 3所示.
 | 图 3 沈阳市2007年至2013年商品住宅特征价格指数增长率趋势图 Fig. 3 Growth rate trend chart of Shenyang commercial housing hedonic price index from 2007 to 2013 |
沈阳市商品住宅价格指数仅对市内五区商品住宅进行取样,结论仅对市内五区商品住宅有效.从商品住宅价格指数增长率的变化情况可以看出,沈阳市商品住宅价格虽然还有上涨空间,但已经明显表现出增速减缓,说明沈阳市的商品住宅市场已经快接近繁荣期的顶峰时段,根据价值规律,在可见的未来,沈阳市商品住宅价格势必会下调.房价增幅减缓并不意味着房地产市场崩盘,市场应注意引导相关企业注重品质提升进而提升竞争力.
沈阳市商品住宅价格增速减缓,有效地抑制了房价的进一步上涨,阻止了房地产泡沫的进一步加大,在未来的一段时间内,房价会在相对低位运行,市场应加强管理,确保逐渐消化掉危险泡沫.
市场繁荣期过后,房地产相关企业的数量会减少,这必然会反作用到房地产业上,使其发展受到阻碍.为了保证沈阳市房地产市场的稳定,可加大、加快保障房建设.这样做,不但可以保证中低收入家庭能够安居乐业,同时可以保存一批有实力、有优势的房地产企业顺利度过低迷期.
随着市场逐渐走向低迷,商品住宅售后的物业管理工作势必会受到影响,加上各种买房时没有发现的问题在居住时逐渐表现出来,这对后期物业管理造成更大压力.政府相关部门应该规范物业管理,并适时进行人员培训,加强责任感教育,提升物业管理水平.
| [1] | Boyle M A, Kiel K A.A survey of house price hedonic studies of the impact of environmental externalities[J]. Journal of Real Estate Literature, 2001, 9(2):117-144.( 1) 1) |
| [2] | 洪开荣, 杨晨.国内外房地产特征价格研究方法评述[J]. 山东工商学院学报, 2013, 27(4):9-13. (Hong Kai-rong, Yang Chen.Research method comment of real estate hedonic price at home and abroad[J]. Journal of Shandong Institute of Business and Technology, 2013, 27(4):9-13.)( 1) 1) |
| [3] | Feenstra R C, Shapiro M D.Introduction to “scanner data and price indexes”[M]. Chicago:University of Chicago Press, 2003:1-14.( 1) 1) |
| [4] | Gourieroux C, Laferrere A.Managing hedonic housing price indexes:the french experience[J]. Journal of Housing Economics, 2009, 18(3):206-213.( 1) 1) |
| [5] | Brasington D M, Hite D.A mixed index approach to identifying hedonic price models[J]. Regional Science and Urban Economics, 2008, 38 (3):271-284.( 1) 1) |
| [6] | Jacobsen D H, Naug B E.What drives house prices?[J]. Economic Bulletin, 2005, 76(4):29-41.( 1) 1) |
| [7] | 李巧芝.石家庄市区住宅特征价格模型的构建与分析[J]. 统计与管理, 2011(4):78-80. (Li Qiao-zhi.Construction and analysis of Shijiazhuang urban housing hedonic price model[J]. Statistics and Management, 2011(4):78-80.)( 1) 1) |
| [8] | Adnersson H, Jonsson L.Property price and exposure to multiple noise resource:hedonic regression with road and railway noise[J]. Environment and Resource Economics, 2010, 45(1):73-89.( 1) 1) |
| [9] | Theebe M A J.Planes, trains and automobiles:the impact of traffic noise on house prices[J]. Journal of Real Estate Finance and Economics, 2004, 28(2/3):209-234.( 1) 1) |



