风力机专用翼型是在航空翼型的基础上发展起来的.比较著名的有几种:美国NREL的S系列[1],荷兰的DU系列[2,3]以及瑞典FFA的FFA-W系列,丹麦RISФ的RisФ系列[4].Gopalarathenam等 [5]发展了一种可用于多点设计的反设计法,可以根据流体约束确定相应的不同翼型段.Drelaf[6]基于牛顿法编写了XFOIL程序用于翼型设计.Veers等[7]提出了一种尺寸较短、尾部平滑的新型翼型,通过分析表明这种翼型具有更高的升力系数.丹麦RISФ的Fuglsang等[8]
采用XFOIL软件以及数学方法分别对RisФ系列翼型进行优化分析,优化主要是从前缘入手.Ribeiro等[9]采用2条B样条分别表达翼型的上下表面,每个样条用6个控制点.余莉等[10]在ISIGHT平台下通过基准航空翼型NACA4412和固定的前后缘点一起确定翼型形状.现有翼型表达大都是基于控制点和原有成熟翼型,优化时对翼型形状参数进行局部调整.在前人研究基础上,本文从翼型的底层形状表征寻求方法,寻找一种设计空间丰富且可控、包含多样翼型曲线的通用表示形式.
基于位势流和无黏流的流场分析不能反映真实流动的物理机制.CFD求解的是黏性可压N- S方程,能够更加细致地模拟翼型绕流的物理特征本质.文献[11]在ISIGHT平台下采用基于基准翼型的动网格方法执行优化设计,文献[12]在HyPerworks软件下基于网格变形进行翼型优化.本文采用集成表达,在富含各种可能翼型的设计空间内选取种群.在优化中种群变化较大,翼型的变化空间比较大,基于动网格的方法不太适用,此处采用大变形网格重构技术.最终基于通用型线理论和多学科设计方法,得到了相对厚度18 % 翼型,并分析其性能.
1 翼型参数化型线表达理论基于Joukowski保角变换的通用翼型表征形式[13,14,15]是一种易于优化和扩展构成的翼型表达形式.基于Joukowski保角变换思想,复平面Z上的一偏心圆Zc可以变换成另一复平面上类似翼型的曲线:


 |
图1 翼型变换 Fig.1 Airfoil transformation |
基于西奥道生的表达思想,采用一个简单并且通用的拟圆公式:


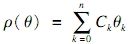 .通过选取不同的Ck就可以表达任意形状的翼型.
2 集成耦合设计流程
.通过选取不同的Ck就可以表达任意形状的翼型.
2 集成耦合设计流程为了实现集成设计,流程分为自编程序耦合翼型形状生成、ICEM网格划分、FLUENT流场分析、优化设计4个子模块.耦合设计流程如图2 所示:1) 由翼型形线表达理论生成翼型形状数据文件,并将符合要求的翼型坐标点通过I/O操作保存为文本文件;2) ICEM调用翼型形状数据文件,读入命令流文件,自动重构网格并生成非结构网格输出;3) 流场计算模块调用网格,设置翼型气动计算各流场参数,气动计算收敛后将气动系数I/O存档于数据文件;4) 读取气动数据文件,计算适应度值,然后进行相应的遗传算法交叉变异等操作,得到新的翼型函数系数,使新的系数有利于产生高适应度值的翼型.再由新的翼型函数系数,得到新的翼型数据.重复步骤1)~4) ,判断是否满足终止准则,若不满足则继续生成新一代种群,直到优化收敛.
 |
图2 集成耦合设计流程 Fig.2 Coupling design chart flow |
计算域网格重构在ICEM中进行,应用分块组合网格技术,划分不同部件和区域,设置不同部件上网格节点的分布规律,进而控制此区域网格疏密等属性.再构成一个整体流场网格,划分情况如图3所示.将组合生成的整体网格转化为FLUENT可以识别的非结构网格.
 |
图3 流场网格 Fig.3 Grids of flow field |
采用分块组合划分,在不同区域采用不同精度的网格,对流场参数变化梯度比较大的敏感区域(翼型前后缘及边界层)以及尾流区域进行加密.保证计算精度基础上极大减少计算资源,这对于多达几千次的优化计算来说尤为重要.翼型表面边界层网格划分情况如图4,图5所示.翼型表面第一层网格高度为1×10-5m,增长率为1.17,共30 层边界层网格.表面Y+值控制在在10以内[16,17,18].
 |
图4 翼型附近网格 Fig.4 Grids near airfoil |
 |
图5 边界层网格 Fig.5 Boundary layer grids |
采用二维连续性方程和二维不可压缩N-S方程.质量守恒方程为

动量守恒方程为

气动计算在FLUENT中完成,编程读入网格文件、设置边界条件等各种流场及计算参数的设置.采用二维双精度定常求解器,分离式求解器求解稳态N-S方程.选取S-A湍流模型,控制方程对流、压力等项均采用二阶格式进行离散,速度和压力耦合采用SIMPLE算法.无穷远处来流速度为入口边界条件,施加给图3中左侧、上侧、下侧三个边界;标准大气压强为出口边界条件,加给图3中右侧边界;翼型边界条件为标准无滑移壁面,收敛精度标准为10-6.
为了验证本文流场计算方法的可靠性,本文计算了WT180翼型[19]在43.822m/s工况风速下的气动性能,并在攻角-8°,0°,25°下与该翼型在西北工业大学NF-3风洞得出的试验结果进行对比,翼型表面压力分布如图6所示.在-8°和0°攻角下,计算的压力系数分布与实验值在大部分区域高度一致.在25°攻角下,由于大分离非稳态流动特性,在翼型前缘吸力面计算和实验差别较大.由于本文在设计攻角下优化翼型,不涉及大分离流动状态,所以验证了CFD方法的可信性和精确性.
 |
图6 三种不同攻角下的压力分布对比 Fig.6 Comparison of pressure distribution at three different attack angles |
叶片展向的70 % ~90 % 处为主要功率产生区域,本文优化相对厚度为0.18的叶尖翼型.叶尖翼型应有较高的升阻比,有助于减小风轮实度、增大启动力矩.以翼型在设计攻角αd下升阻比最大作为目标函数:

设计工况雷诺数Re=3×106,马赫数Ma=0.102,光滑翼面条件.考虑翼型设计空间覆盖特性和型线自由度特性的影响,选取ρ θ 第2到第9项系数作为设计的变量:

翼型型线的设计空间要足够大,这样才能选出优秀种群.边界约束条件为

为使变换后翼型具有前圆后尖、表面光滑过度以及尾缘闭合的流线型特性,复平面上拟圆需通过变换奇点(a,0),x轴方向偏置ε×a,y轴方向偏置 ,则翼型设计的形状函数控制方程(系数控制方程)为
,则翼型设计的形状函数控制方程(系数控制方程)为

翼型应具有较高的升力系数,设计攻角下翼型的升力系数

翼型气动扭矩中心一般在0.25倍弦长位置.考虑与其他翼型的相互兼容性和扭矩特性,翼型最大厚度位置的约束条件为

为控制风轮工作时的噪声,翼型应具有尖尾缘特性:

采用改进遗传算法,当种群规模取值较大时,全局搜索能力增强,收敛所需代数降低;但它并不是愈大愈好,当种群规模增大时,收敛时间在开始会降低;当种群达到一定规模,收敛时间又会上升.进化代数取得较大时,对种群规模的要求也会降低.本文的变量有8个,取种群规模约为变量个数的4倍(30).根据程序调试,取最大进化代数200代、初始交叉算子为0.7、初始变异算子为0.2.在标准遗传算法中,交叉与变异概率是固定点.当变异和交叉的概率较大时,会破坏已经得到的优良个体,而概率较小时会依赖于初始种群的选择,会引起种群未成熟收敛现象.因此需要在进化中,不断控制交叉变异操作.本文算法在进化开始保持当前一个最优解、采用初始交叉变异概率,随着进化进行,逐渐增加最优解的保留个数,减小交叉变异概率、搜索步长,此举既能扩大搜索空间,又不破坏已经得到的最优解,能迅速逼近最优解,且避免震荡的产生.优化得到了相对厚度为0.180的性能优良的风力机专用翼型CF180.
表1给出了CF180及两种相同厚度的国际知名翼型的几何特性,翼型轮廓对比如图7所示.与NACA633-418翼型、DU96W180翼型对比,CF180翼型Tmax在弦长方向29.0 % ,而另外两者分别为34.5 % ,35.5 % .CF180的最大厚度处更靠近翼型气动中心,且具有更大的前缘半径和上翼面厚度,这有利于翼型气动性能的提高.CF180的最大弯度为0.063,NACA633-418,DU96W180分别为0.044,0.050.
| 表1 各翼型几何参数 Table 1 Geometrical parameter of airfoils |
 |
图7 各翼型形线对比 Fig.7 Comparison of airfoil profiles |
图8所示为三种翼型在相同工况条件下(雷诺数Re=3×106,马赫数Ma=0.102,同为自由转捩或固定转捩条件模拟粗糙或光滑翼面条件)、不同攻角范围内的气动特性对比.在主要攻角范围内,粗糙壁面以及光滑条件下,CF180新翼型的升力系数和升阻比都大于NACA633-418翼型和DU96W180翼型,主要气动参数见表2.
自由转捩工况时,CF180在攻角为11°时取得最大升力系数1.690,在攻角为5°时获得最大升阻比160.840,大幅优于NACA633-418的1.416(攻角为13°)和136.167(攻角为5°),增幅分别为19.4 % 和18.1 % .DU96W180在攻角为11°有最大升力系数1.287,在攻角为6°有最大升阻比158.651.CF180相对DU96W180的增幅分别为31.1 % 和1.4 % .虽然从最大升阻比数据看,相对增幅较小,但从0°到13°攻角范围内看,升阻比平均提高了39.5 % .
 |
图8 各翼型的气动性能 Fig.8 Aerodynamic performances of airfoils |
| 表2 各翼型气动参数 Table 2 Aerodynamic parameter of airfoils |
固定转捩工况时,吸力面1 % 弦长位置处施加固定转捩(Xtrs=0.01),压力面10 % 弦长位置处施加固定转捩(Xtrp=0.01)模拟翼型粗糙条件.CF180在攻角为11°时取得最大升力系数1.540,在攻角为7°时获得最大升阻比91.057.NACA633-418在攻角为13°时取得最大升力系数1.363,在攻角为7°时获得最大升阻比79.551.CF180相对NACA633-418的增幅分别为13.0 % 和14.5 % .DU96W180在攻角为12°时取得最大升力系数1.257,在攻角为7°时获得最大升阻比76.654.CF180相对DU96W180的增幅分别为22.5 % 和18.8 % .可看出叶片表面粗糙度增加时,新翼型仍可保持较高升力系数和升阻比.综上所述,新翼型在设计工况和非设计工况下、主要攻角范围内有较高的升力系数和升阻比.
4 结论1) 采用通用翼型形线表达和CFD相结合的方法,体现了集成表达使用方便、设计空间丰富且可控的优点.
2) 耦合翼型生成、网格重构、边界条件生成和流场解算,摆脱了控制点、初始翼型和流场计算等方面的限制因素.
3) NACA翼型是低攻角航空翼型,对于风力机来说性能明显较差.DU96W180翼型是风力机知名翼型,尤其在失速段表现良好.CF180新翼型在设计和非设计工况下都有良好的气动性能.
| [1] |
Tangler J L,Somers D M.Status of the special purpose airfoil families [C]// Proceedings of WINDPOWER’87.San Fransisco,1987:229-335.
( 1) 1)
|
| [2] |
Timmer W A,van Tooij P.Summary of the Delft University wind turbine dedicated airfoils [J].Journal of Solar Energy Engineering,2003,125(4):488-496
( 1) 1)
|
| [3] |
Van Rooij R,Timmer W A.Roughness sensitivity considerations for thick rotor blade airfoils [J].Journal of Solar Energy Engineering,2003,125(4):468-478
( 1) 1)
|
| [4] |
Fuglsang P,Bak C,Gaunaa M,et al.Design and verification of the RisФ-B1 airfoil family for wind turbines[J].Journal of Solar Energy Engineering,2004,126(4):1002-1010
( 1) 1)
|
| [5] |
Gopalarathenam A,Selig M S.Multipoint inverse methods for multielement airfoil design[J].Journal of Aircraft,1998,35(3):398-404
( 1) 1)
|
| [6] |
Drela M.XFOIL:an analysis and design system for low Reynolds number airfoils[M].Berlin:Springer Heidelberg,1989:1-12.
( 1) 1)
|
| [7] |
Veers P S,Ashwill T D,Sutherland H J,et al.Trends in the design,manufacture and evaluation of wind turbine blades[J].Wind Energy,2003,6(3):245-259
( 1) 1)
|
| [8] |
Fuglsang P,Bak C.Development of the Ris wind turbine airfoils [J].Wind Energy,2004,7(2):145-162
( 1) 1)
|
| [9] |
Ribeiro A F P,Awruch A M,Gomes H M.An airfoil optimization technique for wind turbines[J].Applied Mathematical Modelling,2012,36(10):4898-4907
( 1) 1)
|
| [10] |
余莉,呼政魁,程涵,等.风力机翼型的多学科设计优化[J].南京航空航天大学学报,2011,43(5):697-700.(Yu Li,Hu Zheng-kui,Cheng Han,et al.Multidisciplinary design optimization for wind turbine airfoil[J].Journal of Nanjing University of Aeronautics & Astronautics,2011,43(5):697-700.)
( 1) 1)
|
| [11] |
朱雄峰,郭正,侯中喜,等.基于动网格的翼型设计优化[J].国防科技大学学报,2013,35(2):1-6.(Zhu Xiong-feng,Guo Zheng,Hou Zhong-xi,et al.Dynamic mesh based airfoil design optimization[J].Journal of National Universityof Defense Technology,2013,35(2):1-6.)
( 1) 1)
|
| [12] |
闵新勇,董湘怀,邬旭辉.基于网格变形法的风机翼型气动性能优化[J].太阳能学报,2011,32(9):1303-1308.(Min Xin-yong,Dong Xiang-huai,Wu Xu-hui.Aerodynamic optimization of a wind turbine airfoil by mesh morphing technique[J].Acta Energiae Solaris Sinica,2011,32(9):1303-1308.)
( 1) 1)
|
| [13] |
Wang Q,Chen J,Pang X,et al.A new direct design method for the medium thickness wind turbine airfoil[J].Journal of Fluids and Structures,2013,43:287-301
( 1) 1)
|
| [14] |
Cheng J,Zhu W,Fischer A,et al.Design and validation of the high performance and low noise CQU-DTU-LN1 airfoils[J].Wind Energy,2013,17(12):1817-1833
( 1) 1)
|
| [15] |
Chen J,Zhang S Q,Hou Y,et al.Parametric geometry representations for wind turbine blade shapes[J].High Technology Letters,2011,17(3):325-332.
( 1) 1)
|
| [16] |
Chen J,Wang Q,Pang X,et al.Improvement of airfoil design using smooth curvature technique[J].Renewable Energy,2013,51:426-435
( 1) 1)
|
| [17] |
Lanzafame R,Mauro S,Messina M.Wind turbine CFD modeling using a correlation-based transitional model[J].Renewable Energy,2013,52:31-39
( 1) 1)
|
| [18] |
Ram K R,Lal S,Ahmed M R.Low Reynolds number airfoil optimization for wind turbine applications using genetic algorithm[J].Journal of Renewable and Sustainable Energy,2013,5(5):052007,1-15
( 1) 1)
|
| [19] |
张石强,陈进,沈文忠,等.基于多目标遗传算法的风力机翼型形状优化[J].太阳能学报,2011,32(8):1269-1274.(Zhang Shi-qiang,Chen Jin,Shen Wen-zhong,et al.Multi-objective optimization of wind turbine airfoil profile based on genetic algorithm[J].Acta Energiae Solaris Sinica,2011,32(8):1269-1274.)
( 1) 1)
|




