露天矿工程量(包括采剥量、堆放量等)计算是矿山测量验收工作中的一项重要工作，对加强矿山生产监控和成本管理具有重要意义.目前露天矿工程量计算方法主要有断面法、格网法、等高线法和DTM三角网差值法等^[1].其中，断面法实施工序复杂、工作量大，计算精度受限于外业测量的横断面密度及平行度，主要适用于狭长地带；格网法外业工作量大，计算精度取决于格网间距及地形坡度，较适用于地形平坦的矿山；等高线法要求等高线为闭合曲线，且需与断面法结合使用，较适用于地形坡度变化较大的矿山；而DTM三角网差值法可真实地反映地表特征，计算精度高，已得到广泛应用^{[1, 2]}.

采用DTM三角网差值法的前提是获取地形数据.目前露天矿山地形数据采集主要利用全站仪、GPS-RTK测量或远距地面LiDAR扫描等.然而，全站仪、GPS-RTK测量工作量大且GPS信号强度易受距离及环境干扰；远距地面LiDAR设备昂贵，且对架站场地要求高，地形数据采集存在困难.小型无人机的快速发展及其在矿山测量中的应用大大提高了地形数据的采集效率.Liu等^[3]利用低空无人机影像构建了矿山DTM，并评估了模型精度；McLeod等^[4]利用旋翼无人机获取的视频帧序列重建出露天矿山三维点云，并用于测量断层方向.

本文利用低空旋翼无人机影像\视频帧序列与计算机视觉理论结合，研究了露天矿山无人机影像三维重建及多期点云配准方法，实现了一套完整的自动化、低成本、高效的露天矿山工程量计算新模式.

计算机视觉中，运动恢复结构(structure from motion，SfM)是指从二维图像或视频帧序列中恢复出相应的三维信息，包括成像摄像机姿态参数、场景结构等^[5].其主要过程如下：

首先，在影像序列中提取特征点集，并构建描述子，用于存储特征点相似度计算的空间向量.目前使用比较广泛的特征点提取算法有SIFT (scale-invariant feature transform)^[6]，SURF(speed-up robust features)^[7]等.

其次，利用基于K-D树的近似最邻近(approximate nearest neighbors，ANN)算法计算邻域范围内特征点间描述子的欧式距离差，进行特征点相似度判断，初步确定有匹配关系的特征点对集FM_set={(f,f′)}^[5].其中,(f，f′)为某目标影像与其待匹配影像间的一对粗匹配特征点.

然后，采用随机抽取一致性(random sample consensus，RANSAC)^[8]策略和8点算法^[9]相结合，剔除误匹配点，建立满足几何约束的精匹配特征点对集.

继而，采用透视投影，将点云坐标投影到像平面坐标，计算投影误差的目标函数为

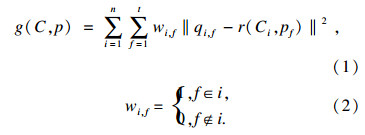
最后，采用基于Levenberg-Marquardt算法的稀疏光束法平差(sparse bundle adjustment,SBA)^[10]解决目标函数的非线性最小二乘问题.通过逐步迭代，不断最小化投影点与观测图像点之间的重投影误差g(C,p)，解算出最佳相机位置、姿态，进而恢复场景三维结构^[5].

为增强重建点云密度，本文基于SfM稀疏点云，采用多目立体视觉(patch-based multiple view stereopsis,PMVS)^[11]算法计算稠密点对匹配关系，构建稠密匹配特征点集，并采用三角化技术，恢复场景致密三维点云.

基于影像重建的点云为独立坐标系，为计算矿山工程量，需将点云转换到用户坐标系，本文利用均匀布设在地面的控制点进行坐标转换.此外，以后期点云为基准，通过选取同名标识点将前期数据转换到统一坐标系，完成点云粗配准.

点云精配准是在粗配准的基础上进一步优化转换参数，即缩放比例k、转换矩阵R及平移系数T，提高配准精度的过程.其中，贡献最突出的是Besl 和Mckay^[12]提出的迭代最近点(interative closest points,ICP)算法，通过寻找两个点集的对应匹配关系，计算坐标转换参数，来完成匹配过程.由于矿山生产过程中，两期点云的形态发生了变化，全局点云配准易出现局部最优，导致配准误差较大.因此，本文设计了一种基于形态不变区的点云配准方法.主要思想：首先，选取两期数据中形态未发生变化的区域，通过ICP算法计算全局最优的转换参数k，R，T.然后，利用上述转换参数对形态发生变化的区域进行刚性转换，完成点云精配准.

此外，为提高匹配效率，迭代匹配过程增加了法向量的方向约束^[13]，具体过程如下：

1) 建立重叠区域内的待匹配面：首先将点云分割成大小相等的区域(立方体)，并分别拟合成面.

2) 阈值判断：若区域内的所有点到拟合面的距离方差小于某阈值T₁，则保留该平面，同时计算其法向量，记为n.反之，则将该区域等分成8块子区域，分别拟合成子平面.

3) 重复步骤2)：当图块包含的点数少于某阈值T₂时，停止判断.

4) 寻找同名匹配点：设基准点集为I={x₀,y₀,z₀,n₀}，在待匹配点集中搜索邻域d范围内的匹配点J = {x,y,z,n}，据文献[13]则有：

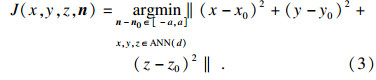
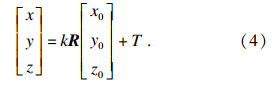
5) 计算转换参数：通过迭代最小化匹配点间的距离差G，计算参考转换参数.

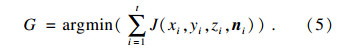
当某次迭代的距离差与上一次迭代结果的差值小于阈值ε时，停止迭代，得到最终的转换参数，用于全局点云配准.

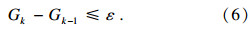
无人机影像具有分辨率高、重叠度大、连续性强等特点，为SfM特征提取与匹配提供了有力保障.为验证本文方法的有效性，选取福建某金属露天矿进行实验.采用八旋翼无人机(BNU D8-1)，手动遥控对堆建中的某矿堆场进行间隔航拍(图 1)，获取该堆场的高重叠、多角度影像.同时记录航拍间隔内矿车运矿量，作为该矿堆土方量变化的标准值.两期数据采集间隔4h，航拍高度约为50m.为测试不同影像类型对SfM重建效果的影响，两期无人机数据获取分别选用不同传感器(表 1).其中，前期数据为较低分辨率的视频帧影像，分辨率为2.7cm×2.7cm；后期数据为高分辨率数码影像，分辨率为1cm×1cm.为尽可能保证两期数据的重建效果一致，选取前期视频影像84帧，后期影像32幅，分别进行点云重建，详见表 1.

图 1(Figure 1)

Fig. 1

图 1 实验区及数据采集 Fig. 1 Experimental area and data acquisition

表 1

Table 1

表 1(Table 1)

表 1 传感器及实验数据 Table 1 Sensors and data set 参数 前期数据 后期数据 采集时间 2013-07-109:30am 2013-07-1013:40pm 相机型号 Sony PJ 790 Canon EOS 50D Mark Ⅱ 航拍高度/m 50 50 影像尺寸/像素 1920×1080 5616×3744 影像分辨率/cm 2.7×2.7 1×1 影像数量 84帧 32幅

表 1 传感器及实验数据 Table 1 Sensors and data set

图 2为利用SfM和PMVS算法生成的堆场三维点云.其中，图 2a为利用前期视频帧影像重建的点云模型；图 2b为利用后期影像重建的点云模型.两期点云密度存在较大差异，分别约为60,290点/m².点云的重建密度主要取决于参与重建的影像分辨率，分辨率越高，地物细节越明显，单位面积内提取的特征点越多，进而完成精匹配恢复重建的点密度越大.

图 2(Figure 2)

Fig. 2

图 2 基于无人机视频帧和影像序列的三维重建点云 Fig. 2 Three dimensional point clouds generated from UAV video frames and UAV images (a)—无人机视频帧重建点云； (b)—无人机影像重建点云.

为评估无人机影像重建点云模型的精度，以后期影像重建点云为例，利用均匀布设在地面的12个控制点将点云转换到用户坐标系，评估点云模型精度.

土方量计算主要参考点间的相对位置.为此，本文重点评估模型的相对误差(即计算长度和实际长度之差与实际长度的比值)^[14].如图 3所示，重建模型的点间相对误差主要分布在±1%范围内.

图 3(Figure 3)

Fig. 3

图 3 UAV影像重建模型的相对精度 Fig. 3 Relative accuracy of point cloud model from UAV images

图 4为两期点云配准结果.其中，图 4a为选取的形态不变区(主要分布在堆场的顶部和底部)配准结果，配准误差的中误差为4.2mm.图 4b为利用图 4a中的转换参数对全局点云进行刚性转换得到的配准结果.

图 4(Figure 4)

Fig. 4

图 4 点云配准结果(前、后期点云分别用蓝色和粉色表示) Fig. 4 Results of point cloud registration (pre-and post-event point clouds are marked in blue and pink, respectively) (a)—形态不变区点云配准； (b)—全局点云配准.

采用Delaunay算法构建点云DTM.图 5为两期点云DTM叠加分析的结果.结果表明，该矿堆后期点云较前期点云整体呈正增长，点间形变距离主要在0.1~0.8m；在后期点云的顶面与侧面交界处出现局部负增长，这主要是由矿车现场作业轮压、推滚所致.

图 5(Figure 5)

Fig. 5

图 5 目标矿堆的形变量分析 Fig. 5 Change analysis for the study area

为进一步评估矿堆形变监测精度，对本文方法与地面LiDAR(Riegl VZ-4000)扫描的监测结果进行了对比分析.为覆盖整个形变区域，地面LiDAR需多站点扫描，且其对架站场地要求较高，数据采集耗时较长.因此，为减少数据采集过程中矿车运输对评估结果的影响，地面LiDAR扫描选取矿车停运时间段进行，两期扫描间隔18h，每期扫描设置3站.结合矿山生产要求，LiDAR首次扫描时间与无人机第二次数据获取时间近乎同步.此外，由于两期扫描过程中，LiDAR仪器角分辨率设置不同，导致前后期点云密度差异较大，分别约为144，400点/m².

为减小点云密度差异对构建DTM精度的影响，本实验设置影像重建点云与LiDAR点云的采样间隔相同，为0.2m.同时，该采样间隔可确保采样后的点云能反映地形真实特征.此外，为保证点云尽量映射到格网内，本文设置DTM格网大小与点云采样间隔保持一致.

两种方法均以两期作业间隔时间内矿山工程部对矿车运载吨位记录的统计表为准，通过对比体积变化进行评估.实验结果见表 2,由表 2可看出，本文方法监测该矿堆体积变化精度约为92%，而地面LiDAR扫描监测的该矿堆体积变化精度约为93%，两者结果基本一致.

表 2

Table 2

表 2(Table 2)

表 2 不同时间间隔内基于本文方法与LiDAR扫描的矿堆体积变化检测结果 Table 2 Results of volume change detection of one stockpile yielded using LiDAR scanning and the proposed method within different time intervals 方法 时间间隔/h 体积变化量参考值/m3 体积变化量检测值/m3 体积变化检测绝对差值/m3 精度/% 本文方法 4 462 424.6 37.4 91.9 LiDAR扫描 18 3102 3318 216 93.0

表 2 不同时间间隔内基于本文方法与LiDAR扫描的矿堆体积变化检测结果 Table 2 Results of volume change detection of one stockpile yielded using LiDAR scanning and the proposed method within different time intervals

本文提出了一种利用无人机影像序列的露天矿山工程量计算方法.首先，针对低空无人机影像分辨率高、重叠度大的特点，采用计算机视觉原理，通过特征匹配实现了露天矿山三维场景重建，有效地克服了传统地形数据采集中存在的困难.其次，针对矿山开采过程中局部形态发生变化的特点，设计了一种基于形态不变区的点云配准方法，保证了矿山多期点云配准精度.最后，通过实例与两期地面LiDAR扫描及矿部统计得到的某矿堆体积变化监测结果进行了对比，对比结果表明，该方法提高了工作效率，保障了矿堆体积变化监测精度，并形成了露天矿山工程量计算评估新模式.

致谢：紫金矿业集团紫金山金铜矿测量科兰万灵科长、舒德福副科长提供了现场帮助，临沂风云航空科技有限公司协助了无人机飞行作业.