Corresponding author: LI Yang-long, E-mail: yanglong.xlnm@163.com
高炉下部调节主要是调节风口尺寸、鼓风参数和喷煤量,维持下部合理的煤气量和均匀的煤气流分布,使炉缸周向工作均匀,并保持整个炉缸具有活跃的工作状态.大型高炉由于炉缸直径大,风口数目多,操作过程中容易发生炉缸圆周方向气流不均、炉缸不活等问题,进而影响煤气流的均匀分布乃至上、下部调节的配合.在调整风口鼓风参数的过程中,对于如何调整风口长度和风口面积存在一定的争议.事实上,高炉风口的风量、风速和鼓风动能的大小与风口中流体流动过程的阻力有密切关系.
现场操作者对于高炉下部调节已有一些操作实践和经验[1, 2],由于高炉下部实验和监测的复杂性和困难性,研究者主要通过数值模拟的方法分析了高炉炉缸内部的工作状态[3, 4, 5, 6, 7, 8],但是目前仍然没有一个完整的、统一的风口风量分配数学模型.通过正确调整风口长度和风口面积,实现高炉风口风量的合理分配,显得十分重要和迫切.
1 高炉风口风量分配数学模型 1.1 风口压力损失高炉热风总管与热风围管连接,各送风支管、鹅颈管、弯头、直吹管及风口小套等设备构成热风输送系统,与高炉直接相通,如图 1a所示.除风口小套以外,每个风口位置的送风支管、直吹管等设备结构设计相同.由于主要分析风口小套长度或面积对风口鼓风参数的影响,因此不考虑热风围管、送风支管等设备热风的压力损失,则高炉风口可简化为一个由各风口小套组成的并联管路,各风口热风的压力损失相等且等于总压差,如图 1b所示.
 | 图 1 高炉热风管道及风口并联示意图 Fig. 1 Schematic of hot blast pipes and parallel tuyeres (a)—高炉热风管道示意图; (b)—风口并联示意图. |
假设高炉有n个风口,风口沿程的压力损失和局部压力损失按式(1)计算:

定义风口的综合阻力系数  ,则有
,则有

由于各个风口的连接方式属于并联管路,并联风口的压力损失和质量流量满足如下关系:

由式(3)知,并联管路的阻力损失可以表示为

参考电阻、热阻的定义,不妨提出适合风口管道流动的流阻的概念,定义式为

由于流动的复杂性,流阻为压力损失的平方根与流量之比,表示风口对流体流动阻碍作用的大小,单位为kg1/2·m-7/2.对比式(4)和式(5)可知:

音速的计算公式为  ,其中R为气体常数,k为绝热指数.对于热风而言,R=286.7,k=1.4,得到1 200 ℃时热风中的音速为769 m/s,热风速度远小于当地音速,可将热风近似为不可压缩流体.
,其中R为气体常数,k为绝热指数.对于热风而言,R=286.7,k=1.4,得到1 200 ℃时热风中的音速为769 m/s,热风速度远小于当地音速,可将热风近似为不可压缩流体.
大高炉风口直径一般在110~150 mm,风口绝对粗糙度约为6.3 μm,鼓风压力约在0.4~0.5 MPa内.分别计算了两种风口直径(110,150 mm)在两种压力(0.4,0.5 MPa)条件下,鼓风速度与雷诺数及沿程阻力系数的关系,如图 2所示.当风口的鼓风速度在200~300 m/s范围时,雷诺数在105量级,根据莫迪图可知,风口的热风流动处于湍流光滑管区,与风口的相对粗糙度无关,只与Re有关,可按式(7)计算沿程阻力系数:

从图 2中可知,鼓风速度在200~300 m/s范围时,沿程阻力系数介于0.011~0.015之间.当风口直径不变时,随着风速增加,风口沿程阻力系数减小;而在相同风速下,风口直径减小,风口的沿程阻力系数增加.由式(7)可以推出式(8):
 | 图 2 风口风速与雷诺数和沿程阻力系数的关系 Fig. 2 Relationship between blast velocity and Reynolds number and frictional resistance coefficient |

又由于


当各风口热风压力和温度相同时,对于任意的i,j风口,有Δpi = Δpj,ρi=ρj,νi=νj(风口并联).继而,有  ,代入整理得到
,代入整理得到

若已知风口j的沿程阻力系数λj,就可以求得风口i的沿程阻力系数λi.
1.4 风口调整后鼓风参数变化在总风量不变条件下,分别调整m (1≤m≤n)个风口长度或者风口面积,计算各风口风量、风速和鼓风动能的变化.进行如下假设:
1) 总风量Q保持不变;
2) 为了定量化计算,不考虑各风口的局部压力损失,局部压力损失的影响在后面讨论;
3) 当调整风口长度时,风口面积不作调整;调整风口面积时,风口长度不作调整.
1.4.1 初始条件
风口调整前,各个风口尺寸相同,各风口流量近似相等,满足:  ,Qi=
Q/n,i=1,…,n.
,Qi=
Q/n,i=1,…,n.
由式(5)可知,风口的流量比实际上是风口流阻比的倒数,则有

使用下标a,u分别表示已调整的和未调整的风口;上标′表示调整后的参数,无上标的变量表示调整前的参数. La′,Lu′分别为调整后,已调整的和未调整的风口长度; da′,du′分别为调整后,已调整的和未调整的风口的直径;Qa′,Qu′分别为调整后,已调整的和未调整风口的体积流量;λa′, λu′分别为调整后,已调整的和未调整的风口的沿程阻力系数.
1) 增加m个风口长度,其余风口尺寸不变,则有La′>La=Lu,Lu′=Lu.
由式(12)可知,风口长度增加后,已调整与未调整的风口的流量比为

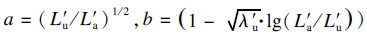 ,得到调整后各个风口的风量:
,得到调整后各个风口的风量:

2) 减小m个风口直径,其余风口尺寸不变,则有da′<da=du,du′=du.
由式(12)可知,风口直径减小后,已调整与未调整的风口的流量比为

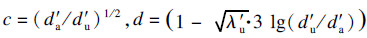 ,得到调整后各个风口的风量:
,得到调整后各个风口的风量:

综合1.4.2节中风口长度和面积的调整,各风口调整前、后的风量比为

各风口调整前、后的风速比为


需要注意的是,式(15)~(17)中,当调整风口长度时,风口面积不作调整(此时c =d =1);调整风口面积时,风口长度不作调整(此时a=b=1).
2 结果分析 2.1 风口流阻分析风口流阻表示风口中流体流动时受到的阻碍作用.风口属于逐渐收缩管,其局部阻力系数采用下式计算:


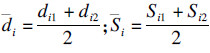 ;di1,di2分别表示第i个风口的入口截面和出口截面的直径.
;di1,di2分别表示第i个风口的入口截面和出口截面的直径.
若风口的鼓风速度为250 m/s,di1,di2分别为180,130 mm,利用式(19)计算在1 200 ℃,0.4或0.5 MPa下的风口流阻,如图 3所示.随着风口长度的增加以及风口直径的减小,风口流阻都表现出逐渐增大的趋势.因此,风口流阻能够正确反映热风在风口中流动所受阻力的大小.
 | 图 3 风口长度和直径对风口流阻的影响 Fig. 3 Influence of tuyere length and diameter on tuyere flow resistance |
某5 500 m3高炉有42个风口,风口长度为620 mm,风口直径为130 mm.从图 2中可知,风口沿程阻力系数的范围约在0.011~0.015,取平均值λu′=0.013作为未调整风口的沿程阻力系数.
图 4所示为调整风口的长度对于鼓风参数的影响,图 4a中已调整的风口长度由620 mm增加至730 mm,图 4b中已调整的风口长度由620 mm减小至510 mm,未调整的风口长度不变.横坐标表示调整的风口个数,纵坐标为调整之后与调整之前的风口鼓风参数的比值.从图中发现:1)增加部分风口的长度后,其风量、风速和鼓风动能都降低,而未调整风口的风量、风速和鼓风动能都提高;2)减小风口长度后,已调整的风口风量、风速、鼓风动能提高,而未调整风口的风量、风速、鼓风动能相应降低;3)当调整全部风口长度时,各风口鼓风参数与调整前相同.
 | 图 4 调整风口长度对鼓风参数的影响 Fig. 4 Influence of adjusting length of tuyeres on blast parameters (a)—增加风口长度; (b)—减小风口长度. |
回旋区深度范围一般在0.8~1.8 m左右[9],回旋区深度的经验公式[10]为

图 5所示在总风量不变的条件下,调整风口直径对风口鼓风参数的影响.缩小风口面积时,已调整的风口直径由130 mm减小至110 mm;增大风口面积时,已调整的风口直径由130 mm增加至150 mm,未调整的风口直径保持不变.
 | 图 5 调整风口直径对风口鼓风参数的影响 Fig. 5 Influence of adjusting diameter of tuyeres on blast parameters (a)—风口风量; (b)—风口风速; (c)—鼓风动能. |
从图 5a可知,减小部分风口直径后,已调整风口的风量降低,而未调整风口的风量提高.随着调整风口个数的增加,未调整的风口的风量逐渐增加,而已调整的风口的风量降低幅度减缓.当增加风口直径时,风口风量的变化趋势正好相反.
图 5b,5c分别为风口直径对风口风速和鼓风动能的影响.风口直径由130 mm缩小至110 mm后,调整的风口个数在1~12个时,已调整风口的风速降低,而未调整的风口风速增加;当调整的风口个数大于12个,已调整的、未调整的风口的风速都增加,但是未调整的风口的风速增加幅度更大.调整的风口个数在1~23个时,已调整风口的鼓风动能降低,而未调整的风口鼓风动能增加;当调整的风口个数大于23个,已调整的、未调整的风口的鼓风动能都增加,但是未调整风口的鼓风动能增加幅度更大.当增加风口面积时,风口鼓风参数的变化趋势正好相反.可见,缩小风口面积不一定能提高该风口的速度和鼓风动能.
3 讨 论 3.1 风口局部阻力损失的影响图 6所示为风口长度和直径对风口流阻的影响,图中R考虑,R不考虑分别表示考虑、不考虑局部阻力损失的风口流阻.考虑局部阻力损失的风口流阻比不考虑局部阻力损失的风口流阻略大.不论是否考虑局部阻力损失,当风口长度增加,或者风口面积减小时,风口流阻都表现出增加的趋势,考虑局部阻力损失的风口流阻约为不考虑局部阻力损失的风口流阻的1.26倍.因此,模型中忽略局部阻力系数的结果仍然可以正确反映调整风口长度或面积后,风口鼓风参数的变化.
 | 图 6 局部阻力系数对流阻的影响 Fig. 6 Influence of local resistance coefficient on tuyere flow resistance |
从前面的分析中可知,缩小部分风口的面积,对应风口的风速和鼓风动能不一定提高,这取决于风口的调整数目和调整尺寸.当调整前后已调整的风口风速不变时,由式(16)可知需满足

整理式(21),得到调整风口面积后,风口风速提高的临界风口个数计算公式:

根据式(17),得到调整风口面积后,风口鼓风动能提高的临界风口个数计算公式:

上式中[]表示向下取整数.利用式(22)和式(23),可以计算实现已调整风口的风速、鼓风动能提高或降低需要调整的风口个数,调整策略列于表 1中.
| 表 1 风口面积改变时的风口风速和鼓风动能调整 Table 1 Adjustment of blast velocity and kinetic energy of tuyere with changing the tuyere area |
1) 提出风口流阻的概念,风口流阻与风口的综合阻力系数、流体密度的平方根成正比,与风口横截面积成反比,表示风口对流体流动阻碍作用的大小.给出风口流阻的计算公式,计算表明增加风口长度和缩小风口面积都会增加风口流阻.
2) 建立了高炉风口风量分配数学模型,分析了某5 500 m3高炉在风口长度改变时,各风口的风量、风速和鼓风动能的变化.发现增加部分风口长度,已调整风口的风量、风速和鼓风动能都将减小,未调整风口的风量、风速和鼓风动能增加;减小部分风口长度,已调整风口的风量、风速和鼓风动能增加,未调整风口的鼓风参数降低.
3) 分析了某5 500 m3高炉在风口面积改变时,各风口的风量、风速和鼓风动能的变化,并提出了已调整风口的风速、鼓风动能增加(或减小)的临界风口调整个数公式.当调整风口个数较少时,已调整风口的风速和鼓风动能降低;当调整多个风口时,已调整风口的风速和鼓风动能才可能增加.而未调整风口的风量、风速和鼓风动能都增加,并且增加幅度远大于缩小面积的风口.
| [1] | Sasaki K, Hatano M, Watanabe M, et al.Investigation of quenched No.2 blast furnace at Kokura works[J]. Tetsu-to-Hagane, 1976, 62(5):580-591.( 1) 1) |
| [2] | 吴狄峰,程树森,赵宏博,等.风口尺寸对高炉操作影响的研究[J].钢铁,2008,43(4):18-23. (Wu Di-feng, Cheng Shu-sen, Zhao Hong-bo, et al.Study on effect of tuyere size on blast furnace operation[J]. Iron and Steel, 2008, 43(4):18-23.)( 1) 1) |
| [3] | 陈辉,张卫东,马泽军,等.高炉送风系统压力损失的理论解析[J].钢铁,2011,46(2):22-25. (Chen Hui, Zhang Wei-dong, Ma Ze-jun, et al.Theoretical analysis on pressure loss in blast system of BF[J]. Iron and Steel, 2011, 46(2):22-25.)( 1) 1) |
| [4] | 王晓鸣,李强,邹宗树,等.利用壅塞原理均匀分配高炉各风口的喷煤量[J].东北大学学报(自然科学版), 2006, 27(9):999-1002. (Wang Xiao-ming, Li Qiang, Zou Zong-shu, et al.Uniformly distributed mass flow rate of PCI into BF tuyeres on formation principle of choking[J]. Journal of Northeastern University( Natural Science), 2006, 27(9):999-1002.)( 1) 1) |
| [5] | Natsui S, Ueda S, Nogami H, et al.Analysis on non-uniform gas flow in blast furnace based on DEM-CFD combined model[J]. Steel Research International, 2011, 82(8):964-971.( 1) 1) |
| [6] | Natsui S, Ueda S, Oikawa M, et al.Optimization of physical parameters of discrete element method for blast furnace and its application to the analysis on solid motion around raceway[J]. ISIJ International, 2009, 49(9):1308-1315.( 1) 1) |
| [7] | Umekage T, Kadowaki M, Yuu S.Numerical simulation of effect of tuyere angle and wall scaffolding on unsteady gas and particle flows including raceway in blast furnace[J]. ISIJ International, 2007, 47(5):659-668.( 1) 1) |
| [8] | Guo J, Cheng S S, Zhao H B, et al.A mechanism model for raceway formation and variation in a blast furnace[J]. Metallurgical and Materials Transactions B, 2013, 44(6):487-494.( 1) 1) |
| [9] | Gupta G S, Rudolph V.Comparison of blast furnace raceway size with theory[J]. ISIJ International, 2006, 46(2):195-201.( 1) 1) |
| [10] | 项钟庸,王筱留.高炉设计-炼铁工艺设计理论与实践[M].北京:冶金工业出版社,2007:171-172. (Xiang Zhong-yong, Wang Xiao-liu.Blast furnace design- theory and practice of ironmaking process design[M]. Beijing:Metallurgical Industry Press, 2007:171-172.)( 1) 1) |




