2. 沈阳新松机器人自动化股份有限公司, 辽宁 沈阳 110168
2. SIASUN Robot & Automation Co., Ltd., Shenyang 110168, China.
Corresponding author: LIU Yu, E-mail: yuliu@me.neu.edu.cn
车削颤振是切削过程中刀具与工件之间的动态切削力激发的自激振动[1].车削颤振不仅破坏加工零件的表面质量,还破坏机床,影响刀具寿命.因此进行车削颤振稳定性预测就显得尤为重要[2, 3].
目前,国内外学者针对车削加工过程的颤振预测理论进行了大量的研究并已形成部分商用化的软件.Tobias和Fishwick提出了车削颤振源于加工系统的不稳定性理论,建立正交切削模型,得到车削颤振预测的稳定性叶瓣图(stability lobe diagram,SLD),给出了转速-切宽加工参数的稳定情况.Altintas等[4]提出了频域稳定性预测方法,采用零次近似和高次近似法得到稳定性叶瓣图,提高了稳定性预测精度.Stépán 等 [5, 6, 7]采用时域预测方法对具有时间延迟的周期线性系统进行研究,提出了半离散方法,提高了预测精度.Ding 等 [8, 9, 10]采用全离散法获得周期线性系统稳定性叶瓣图.
国外,美国的MLI公司进行车削颤振研究并开发了MetalMax系统,通过对刀具的敲击实验,找出车床主轴的最优转速.加拿大的Altintas等 对车削加工过程中的颤振预测进行研究[11],开发了Cutpro软件,对车削等加工过程进行颤振预测.丹麦的B&K公司对车床、铣床进行研究,开发了PULSE测试系统,对车床、铣床振动信号进行采集并得到其频响函数.国内,北京航空航天大学高效数控加工技术研究应用中心主任刘强教授进行相关研究[12],开发了“基于数控加工过程动力学的仿真优化系列软硬件系统——X-Cut”,对数控车床进行颤振预测和仿真优化.但以上软件都不能根据得到的频响函数设置分析频率范围,不能根据用户需求进行叶瓣数等参数设置来绘制稳定性叶瓣图.
本软件基于再生型振动理论[13, 14],采用再生颤振的频域预测方法[15]进行颤振预测,将信号采集与分析结合,实现了振动信号同步触发采集和变参数稳定性叶瓣图[15]绘制的一体化.同时,系统能够进行频率分析范围设置,对输入参数进行判断识别.软件采用C#语言[16]编程,对系统进行了功能模块及界面设计.
1 系统需求分析软件具有能够进行触发信号识别设置、振动信号同步触发采集、设置频响函数分析频率范围、变参数稳定性叶瓣图绘制、图形显示及数据保存等功能.
1.1 车削颤振稳定性预测软件设计的总体目标软件系统涵盖车床测试的整个过程,形成完善的数据采集、数据分析体系.
1.2 车削颤振稳定性叶瓣图算法车削加工系统主要存在x,z两个方向的振动.如果考虑刀尖半径的影响,则需要将切削和力分解到x或z方向上.忽略刀尖半径,则端面车削时以x向振动为主,外圆车削时以z向振动为主.
忽略刀尖半径的端面车削,其车削加工系统动力学模型如图 1所示.相对工件来说,刀架的刚度小很多,所以假设工件为刚性结构.
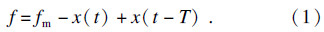

 | 图 1 车削加工系统动力学模型 Fig.1 Dynamics model of the turning system |
对于刀架系统,由图 1可得
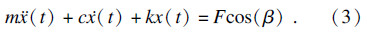
由式(1)~式(3)得
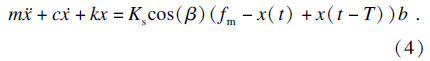
由式(4)得出传递函数:
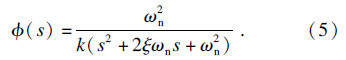
转换成复数域,则传递函数的实部和虚部分别为
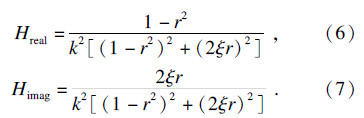
车削过程中的切削稳定性极限为
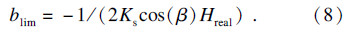
因为切削稳定性极限必须为正数,所以Hreal应为负数,此时刀尖点系统才是稳定切削.
切削过程中主轴转速的计算公式为
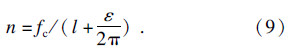
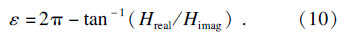
车削颤振稳定性预测软件主要包括信号采集模块和叶瓣图计算模块.由采集卡得到的时域信号经FFT变换变为频域信号,计算得到刀具的频响函数,显示FRF并保存数据.在叶瓣图计算模块中对频响函数进行分析频率范围设置、切削力系数及叶瓣数设置,然后绘制稳定性叶瓣图,显示并保存数据.
2.2 软件界面软件采集模块界面如图 2所示,主要由参数设置部分和绘图部分组成.设置部分包括硬件设置、分析设置、触发设置、力锤加窗、加速度加窗和测试部分.绘图部分依次显示频响函数实部、虚部及相干性.
 | 图 2 采集模块界面 Fig.2 Gathering module interfaces |
车削颤振稳定性预测软件的功能实现主要难题在于触发信号的识别、振动信号同步触发采集的实现、计算稳定性叶瓣图类的设计及绘图功能的实现.
3.1 触发信号的识别信号触发采用上升沿触发方式,即上升沿信号从低于触发滞宽线上升并超过触发电平才为触发信号.软件触发设置如图 3所示,根据力锤敲击的脉冲信号确定触发电平和触发滞宽.图 3中触发电平为5N,触发滞宽为3N.
 | 图 3 系统触发条件设置 Fig.3 Trigger condition setting of the system |
以采样率fs=4 096个/s,预触发样本数为100,样本数N=2 048,触发位置1 000为例,分析信号获取过程如图 4所示.程序每次从PC缓存中读取N个数据存入data中,通过FindTrigger函数寻找触发信号,将不包含触发信号的数据块存入预触发缓存pretrigger中,然后由DAQmx中的异步回调函数从RAM中读取下一个数据块.未找到触发时,将数据存入上次的pretrigger中,继续读取数据,直到找到触发信号.找到触发后,将触发位置前100个数据及剩余的1 048个数据保存到数据表中,继续读入900个数据,保存到数据表中.
 | 图 4 分析信号获取过程 Fig.4 Analytical signal acquisition |
稳定性叶瓣图类包含字段、属性、构造函数和方法.其计算叶瓣图的流程如图 5所示.
 | 图 5 叶瓣计算的流程图 Fig.5 The flow diagram of the lobes calculation |
软件采用了开源的.NET图表类库:ZedGraph,实现了图形的平移、缩放、保存及数值的显示等功能.
4 实验使用该软件在CJ0625车床进行刀尖点测试,得到车床加工系统的位移频响函数.考虑到低频数据对测量结果的影响,故只分析10~400 Hz范围内的频响函数.图 6为加工系统位移频响的实部与对应的虚部.
 | 图 6 CJ0625台式车床加工系统频响函数 Fig.6 FRF of the CJ0625 machine system |
由测试得到的频响函数进行稳定性叶瓣图绘制,得到其在主轴转速ω在500~3 000 r/min时的车削颤振稳定性叶瓣图,如图 7所示.
 | 图 7 主轴转速在500~3 000 r/min车刀的稳定性叶瓣图 Fig.7 Stable lobes at a rotated speed of 500~3 000 r/min |
由图 7可以看出,当转速为1 800 r/min,切宽为2 mm时,加工系统发生颤振.当切宽为1.8 mm时,加工系统稳定.用端面车刀45#钢工件进行切削实验,工件表面如图 8所示,这与预测结果吻合.
 | 图 8 加工表面 Fig.8 Workpiece surface |
1) 基于C#开发了车削颤振稳定性预测软件,研究了频响函数测试过程中多通道高速同步触发采集的实现算法,开发了具有由频域分析方法获得颤振稳定性叶瓣图功能的C#类.
2) 建立了正交车削加工动力学模型,对CJ0625车床的端面车刀进行实验.结果表明车削颤振稳定性预测软件能够对车削颤振进行预测.
| [1] | 刘习军,陈予恕.机床速度型切削颤振的非线性研究[J]. 振动与冲击,1999,18(2):5-9. (Liu Xi-jun,Chen Yu-shu.Nonlinear analysis of speed type cutting chatter of machine tools[J]. Journal of Vibration and Shock,1999,18(2):5-9.)( 1) 1) |
| [2] | 王晓军.车削加工稳定性极限预测的研究[D]. 长春:吉林大学,2005. (Wang Xiao-jun.Study on the prediction of stability limits in turning[D]. Changchun:Jilin University,2005.)( 1) 1) |
| [3] | 曲兴田,吴博达,刘笑羽,等.车削加工中心切削颤振的预报控制[J]. 吉林工业大学学报(自然科学版),1998,28(2):24-28. (Qu Xing-tian,Wu Bo-da,Liu Xiao-yu,et al.The predictive control of cutting chatter at the center of turning process[J]. Journal of Jilin University of Technology (Natural Science Edition) ,1998,28(2):24-28.)( 1) 1) |
| [4] | Budak E, Altintas Y.Analytical prediction of stability lobes in milling[J]. CIRP Annals-Manufacturing Technology,1995,44(1):357-362.( 1) 1) |
| [5] | Insperger T, Stépán G.Updated semi-discretization method for periodic delay -differential equations with discrete delay[J]. International Journal for Numerical Methods in Engineering, 2004,61(1):117-141.( 1) 1) |
| [6] | Insperger T, Stépán G.Semi-discretization method for delayed systems[J]. Internation Journal for Numerical Methods in Engineering,2002,55(5):503-518.( 1) 1) |
| [7] | Elbeyli O, Sun J Q.On the semi-discertization method for feedback control design of linear systems with time delay[J]. Journal of Sound and Vibration,2004,273(1):429-440.( 1) 1) |
| [8] | Ding Y,Zhu L,Zhang X,et al.Second-order full-discretization method for milling stability prediction[J]. International Journal of Machine Tools and Manufacture,2010,50(10):926-932.( 1) 1) |
| [9] | Ding Y,Zhu L,Zhang X,et al.A full-discretization method for prediction of milling stability[J]. International Journal of Machine Tools and Manufacture,2010,50(5):502-509.( 1) 1) |
| [10] | Huang T ,Zhang X ,Ding H, et al.An efficient linear approximation of acceleration method for milling stability prediction[J]. International Journal of Machine Tools and Manufacture,2013,74:56-64.( 1) 1) |
| [11] | Altintas Y,Ko J H.Chatter stability of plunge milling[J]. CIRP Annals - Manufacturing Technology,2006, 55 (1):361-364.( 1) 1) |
| [12] | 赵明,刘强,彭翀.面向制造企业应用的切削数据库研究与开发[J]. 制造技术与机床,2011(6):35-40. (Zhao Ming,Liu Qiang,Peng Chong.Research and development on cutting database for manufacturing enterprises[J]. Journal of Manufacturing Technology and Machine Tool,2011(6):35-40.)( 1) 1) |
| [13] | Taylor F W.On the art of cutting metals[J]. Transaction of ASME,1906,28:31-244.( 1) 1) |
| [14] | Tlusty J, Polacek M.The stability of machine tools against self excited vibrations in machining[C]// Proceedings of the International Research in Production Engineering Conference.New York:ASME,1963:465-474.( 1) 1) |
| [15] | Schmitz T L,Smith K S.Machining dynamics:frequency response to improved productivity[M]. New York:Springer,2009:58-97.( 1) 1) |
| [16] | 钱哨,李挥剑,李继哲.C# WinForm实践开发教程[M]. 北京:中国水利水电出版社,2010:125-156. (Qian Shao,Li Hui-jian,Li Ji-zhe.C# WinForm practice development tutorial[M]. Beijing:China Water Power Press, 2010:125-156.)( 1) 1) |




