Corresponding author: FAN Yun-yun, E-mail: yunyunfan@126.com.
河流海岸工程中的水沙运动是一种常见的自然现象,并伴随有底床冲淤变形等水沙问题的存在,因此了解水沙的运动规律具有重要意义[1, 2, 3, 4, 5].通过得到悬移质泥沙的运动过程,不仅可以找到水流作用下悬移质泥沙运动的发展规律,还可以为引水排沙、河床演变等复杂工程问题提供科学依据.
国内外学者在泥沙模型方面进行了大量研究,并取得了一定的成果[4, 5].但大多数的研究以稳态泥沙浓度分布居多,细致分析讨论其非稳态运动过程以及规律的研究则相对较少.本文首先建立联合k-ε紊流方程和悬沙输运方程的单流体模型,应用该模型分别对净冲刷和净淤积试验进行数值计算,验证了计算模拟的正确有效性.并对试验过程中悬移质泥沙上扬和沉降的运动过程进行了数值模拟,得到试验中悬移质泥沙运动的全过程,并对结果进行分析.
1 水沙运动基本方程 1.1 水流基本方程根据Boussinessq假定,可将垂向二维不可压缩流体的连续方程和雷诺平均的动量方程表示如下:

k-ε紊流模型:


| 表 1 k-ε模型常数取值 Table 1 k-ε model constant value |
本文采用的水沙数学模型为单流体模型,其悬沙输运方程如下:


1) 进出口边界.入口处采用Dirichlet型边界条件,在计算区域的进口断面给定输运变量的初值,出口处采用Neumann型边界条件,所有变量的梯度为0.
2) 壁面边界.水流方程的床面边界条件采用壁面函数法[5].悬沙输运方程的床面边界条件为[5]


3) 自由表面边界.在水流自由表面,流速和紊动动能k的法向梯度为零.紊动耗散率边界条件根据文献 [7] 得到.
悬沙输运方程的自由表面边界条件为[5]

本文选用有限体积数值方法对控制方程进行离散,采用SIMPLE[8]数值方法求解流场,并采用TDMA算法对离散的代数方程组进行数值求解,限于篇幅本文不再做详细介绍.
2 数值模拟 2.1 净冲刷试验数值模拟Van Rijn在1981年进行了净冲刷试验研究[9].试验情况如图 1所示,水槽中床面泥沙颗粒在清水来流作用下上扬直至形成稳定的泥沙浓度分布.试验水槽长30 m,宽0.5 m,高0.7 m,试验水深为0.25 m,水深平均流速为0.67 m/s,床面泥沙粒径D50=0.23 mm,D90=0.32 mm.计算中取D50为代表粒径,相应的沉速ωs=0.22 m/s,床面粗糙高度ks=0.01 m.划分的计算网格水平向长度为0.04 m,竖直向长度为0.01 m.时间步长为0.01 s.
 | 图 1 净冲刷试验示意图 Fig. 1 Sketch of net entrainment from loose bed in the experimental flume flow |
当计算运行到24 s时,泥沙浓度达到稳定状态,其沿程分布如图 2所示.距离冲刷起点处不同位置泥沙浓度沿水深分布的计算值与实测值的比较见图 3.从图中可以看出,计算结果与实测结果吻合良好,验证了模型以及计算的正确有效性.
 | 图 2 泥沙浓度沿程分布最终计算结果(单位:kg/m3) Fig. 2 Calculation results of sediment concentrations longitudinal variations (unit: kg/m3) |
 | 图 3 泥沙浓度计算结果与实测结果对比图 Fig. 3 Comparison of the calculated and measured sediment concentrations |
图 4为试验中不同时刻泥沙浓度的沿程分布计算结果.从图中可以看出,当运行到5 s时,自由水面泥沙浓度几乎为0.而当运行到10 s时,距离起始冲刷点分别为4 m和6.2 m位置处的泥沙质量浓度已经分别达到0.002 kg/m3和0.005 kg/m3.随着运行时间的增加,自由水面沿水平方向的泥沙含量逐渐增大,当运行到20 s时,计算结果已经和稳定状态的泥沙分布结果基本一致.
 | 图 4 不同时刻泥沙浓度的沿程分布计算结果(单位:kg/m3) Fig. 4 Calculation results of sediment concentrations longitudinal variations at different time(unit:kg/m3) (a)—5 s; (b)—10 s; (c)—15 s; (d)—20 s. |
Wang和Ribberink在1990年进行了净淤积试验研究[10].试验情况如图 5所示,试验水槽长30 m,宽0.5 m,在水槽前部通过加沙箱加沙,挟沙水流经过10 m无底孔水槽的调节后进入长为16 m的有底孔水槽.通过多孔床面捕捉沉降的泥沙,致使上扬通量几乎为零.水槽试验水深为0.215 m,水深平均流速为0.56 m/s.计算时按均匀沙处理,泥沙颗粒的沉速取0.006 5 m/s,床面的有效粗糙高度ks=0.002 5 m.进口含沙量条件由水槽实测资料给出,数值求解时由最小二乘法拟合给出.划分的计算网格水平向长度为0.01 m,竖直向长度为0.002 5 m.时间步长为0.01 s.
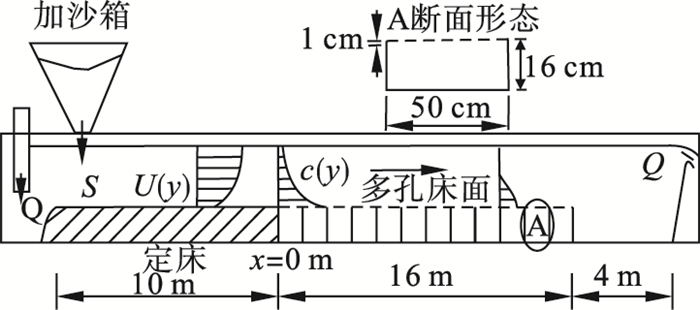 | 图 5 净淤积试验示意图 Fig. 5 Sketch of net deposition on honeycombed bed |
计算运行35 s后,泥沙浓度分布达到稳定状态,稳态泥沙浓度沿程分布结果如图 6所示.距离进口不同位置泥沙浓度沿水深分布的计算值与实测值的比较见图 7.从图中可以看出,计算结果与实测结果吻合良好,验证了计算模拟的正确有效性.
 | 图 6 泥沙浓度分布最终计算结果(单位:kg/m3) Fig. 6 Calculation results of sediment concentrations longitudinal variations (unit: kg/m3) |
 | 图 7 泥沙浓度计算结果与实测结果对比图 Fig. 7 Comparison of the calculated and measured sediment concentrations |
图 8为试验中不同时刻泥沙浓度的沿程分布计算结果.从图中可以看出,当运行到10 s时,距离进口处0~4 m之间的泥沙沉降基本达到稳定状态.当运行到20 s时,距离进口处0~8 m之间的泥沙沉降达到稳定状态,且沿水平方向的浓度梯度随时间增加而逐渐减小.当运行到30 s时,计算结果已经和稳定状态泥沙浓度分布结果基本一致,仅仅在最后的15~16 m内存在差异.
 | 图 8 不同时刻泥沙浓度的沿程分布计算结果(单位:kg/m3) Fig. 8 Calculation results of sediment concentrations longitudinal variations at different time (unit: kg/m3) (a)—10 s; (b)—20 s; (c)—30 s. |
1) 应用联合紊流方程和悬沙输运方程的单流体模型,分别对净冲刷和净淤积试验进行了数值模拟,模拟结果与试验结果基本一致,说明计算模拟正确有效,表明该模型可以用来模拟悬移质泥沙的运动问题.
2) 在净冲刷试验中,泥沙从开始上扬直至稳定状态共运行了24 s.其中,当运行到10 s时,距离起始冲刷点分别为4 m和6.2 m位置处的泥沙质量浓度已经分别达到0.002,0.005 kg/m3.
3) 在净淤积试验中,泥沙从开始沉降直至稳定状态共运行了35 s.其中,当分别运行到10 s和20 s时,距离进口处分别为0~4 m和0~8 m之间的泥沙沉降基本达到稳定状态,且沿水平方向的浓度梯度随时间增加而逐渐减小.
| [1] | Falcini F,Piliouras A,Garra R.Hydrodynamic and suspended sediment transport controls on river mouth morphology[J].Journal of Geophysical Research:Earth Surface,2014,119(1):1-11.( 1) 1) |
| [2] | 李勇,余锡平.基于两相紊流模型的悬移质泥沙运动数值模拟[J].清华大学学报(自然科学版),2007,47(6):805-808.(Li Yong,Yu Xi-ping.Two-phase turbulent flow model for suspended sediment motion[J].Journal of Tsinghua University(Science and Technology),2007,47(6):805-808.)( 1) 1) |
| [3] | 刘诚,沈永明.曲线坐标系下的三维k-ε-Ap固液两相湍流总沙输运模型[J].水力发电学报,2009,28(3):164-170.(Liu Cheng,Shen Yong-ming.A three-dimensional k-ε-Ap two-phase turbulence overall sediment transport model in non-orthogonal curvilinear coordinates[J].Journal of Hydroelectric Engineering,2009,28(3):164-170.)( 1) 1) |
| [4] | 赵东淼,唐军,吴修广.基于Youngs-VOF方法的垂向二维悬沙数值模拟[J].水力发电学报,2013,32(6):99-103.(Zhao Dong-miao,Tang Jun,Wu Xiu-guang.Vertical 2-D numerical model of suspended sediment transport based on Youngs-VOF method[J].Journal of Hydroelectric Engineering,2013,32(6):99-103.)( 3) 3) |
| [5] | Wu W,Rodi W,Wenka T.3D numerical modeling of flow and sediment transport in open channels[J].Journal of Hydraulic Engineering,ASCE,2000,126(1):4-15.( 5) 5) |
| [6] | Van Rijn L C.Sediment transport,part II:suspended load transport[J].Journal of Hydraulic Engineering,ASCE,1984,110(11):1613-1641.( 1) 1) |
| [7] | Krishnappan B G,Lau Y L.Turbulence modeling of flood plain flows[J].Journal of Hydraulic Engineering,ASCE,1986,112(4):251-266.( 1) 1) |
| [8] | Patankar S V,Spalding D B.A calculation procedure for heat,mass and momentum transfer in three-dimensional parabolic flows[J].International Journal of Heat and Mass Transfer,1972,15:1797-1806.( 1) 1) |
| [9] | Van Rijn L C.Mathematical modeling of suspended sediment in non-uniform flows[J].Journal of Hydraulic Engineering,ASCE,1986,112(6):433-455.( 1) 1) |
| [10] | Wang Z B,Ribberink J S.The validity of a depth-integrated model[J].Journal of Hydraulic Engineering,ASCE,1990,116(10):1270-1288.( 1) 1) |




