2. 中国航天标准化与产品保证研究院, 北京 100071
2. China Academy of Aerospace Standardization and Product Assurance, Beijing 100071, China.
履带车辆在凹凸不平的路面上行驶时,负重轮和车体都会产生振动.这些振动影响履带车辆的使用性能,主要表现在影响车辆的行驶平顺性、牵引特性、稳定性及各零部件的疲劳强度和使用寿命.地面-履带-负重轮系耦合系统的激励特性主要表现为负重轮的振动特性,地面-履带-负重轮系耦合系统激励特性作为履带车辆行驶系统的激励输入,在履带车辆的设计研发中具有重要的地位.而影响负重轮振动的因素主要包括履带预张紧力、车辆行驶速度、地面形貌、车辆的质量及车辆悬挂系统参数等[1, 2]. 本文以履带车辆负重轮动位移为研究对象,采用理论推导计算和动力学仿真相结合的方法,分析车辆行驶速度这一因素对地面-履带-负重轮系耦合系统激励特性的影响.
1 不考虑履带影响时负重轮动位移的理论计算影响履带车辆负重轮动位移变化规律的因素多,系统内部关系复杂,且履带结构建模困难,为了计算负重轮动位移车辆行驶速度的变化情况,需构建车辆悬挂系统的动力学模型[3, 4, 5, 6, 7].
1.1 基本假设为了简化问题、便于建模与计算,对履带车辆作如下简化[8, 9, 10].
1) 履带车辆行驶过程中,假定行驶的路面为刚性路面,路面不平度不会因为车辆辗压而发生变化,且左右车辙的不平度函数相同,路面不平度对各轮的振动输入只存在时间延迟.
2) 将履带结构视为一种近似于铺设地面激励的“无限轨道”,不计履带对车体的作用,波长小于履带节距的路面不平度完全被履带板所覆盖.
3) 车体质心关于纵轴线左右对称.车体侧倾振动小,且很快停止,可不计车体的侧倾振动,只考虑车辆垂直运动和俯仰运动,用8自由度平面半车模型建立车辆悬挂系统的力学模型.
4) 车辆采用独立线性悬挂,将悬挂质量分解到悬挂与非悬挂中去,使其简化为弹簧刚度和阻尼.
1.2 半车8自由度动力学模型的建立履带车辆以速度v向右方行驶,选取履带车辆静平衡位置时悬挂质量的质心为动坐标原点,过履带车辆质心的纵轴为x轴,横轴y轴,竖轴为z轴,车体绕过质心的横轴y的俯仰角位移为φ,x,y,z和φ的正向均按右手定则判定.
半车车辆悬挂系统模型见图 1.

|
图1 半车车辆悬挂系统模型 Fig. 1 Model of half-vehicle suspension system |
建立半车动力学方程:


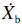 ,
,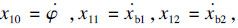
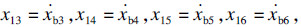 ,则可以建立如下的状态方程:
,则可以建立如下的状态方程:

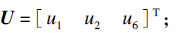

系统的输出向量:

输出方程为

为了书写方便,记


各分块矩阵为


为了研究履带车辆行驶速度对负重轮动位移的影响需对4种典型路面(起伏路、砂石路、戈壁路、铺面路)的不平度进行测试,以构建4种典型路面的仿真模型.由于篇幅限制,本文只列出了起伏土路的测试结果.
根据待测路面的实验条件,选用接触式动态纵断面测试仪器进行路面不平度测试.起伏路路面见图 2,得到的起伏路路面的不平度测试数据见图 3.

|
图2 起伏路路面 Fig. 2 Rough road pavement |

|
图3 起伏路路面不平度测试数据 Fig. 3 Road roughness data of rough road pavement |
测量得到的大量路面不平度随机数据经过数据处理可以得到路面功率谱.
1.4 不考虑履带影响时负重轮动位移的理论估算根据车辆悬挂系统的动力学方程及履带车辆的具体结构参数,利用MATLAB软件平台可以实现负重轮动位移的理论计算,计算流程见图 4.履带车辆以10 km/h的速度行驶时理论计算得到的第一负重轮动位移的功率谱相对值与路面不平度的功率谱相对值对比关系见图 5.

|
图4 计算流程图 Fig. 4 Flowchart of calculation |

|
图5 功率谱相对值对比 Fig. 5 Comparison of relative value for power spectrum |
由负重轮动位移的理论计算结果可知,在低频段,负重轮动位移的功率谱曲线与地面的功率谱曲线相似;在高频段,负重轮动位移的功率谱曲线明显下降,这说明负重轮对地面功率谱中的高频成分有明显的滤波作用.
2 仿真分析不同行驶速度对负重轮动位移的影响利用动力学仿真软件LMS,结合履带车辆参数建立悬挂系统仿真模型,见图 6.结合车辆设计参数,实验结果与仿真结果验证了仿真模型的准确性.

|
图6 履带车辆仿真模型 Fig. 6 Simulation model of tracked vehicle |
采用理论计算时,假设履带车辆的行驶路面不变,研究负重轮动位移随行驶速度的变化规律.动力学仿真时,假设履带车辆的行驶路面不变,研究不同车辆行驶速度下负重轮动位移的变化情况,仿真条件见表 1.
| 表1 仿真条件 Table 1 Simulation conditions |
不同行驶速度下履带车辆负重轮动位移的变化情况(起伏路)见图 7.对不同行驶速度下的负重轮动位移仿真结果进行统计分析,并结合不考虑履带影响的负重轮动位移理论计算结果,得到负重轮动位移相对值的统计数据见表 2.车辆行驶速度为30 km/h时,第一负重轮位移分布见图 8.

|
图7 第一负重轮的动位移 Fig. 7 Dynamic displacement of the first road wheel |
| 表2 第一负重轮动位移统计数据表 Table 2 Statistics table of dynamic displacement for the first road wheelmm |

|
图8 第一负重轮动位移分布直方图 Fig. 8 Histogram of dynamic displacement distribution for the first road wheel |
根据负重轮动位移的仿真结果及不考虑履带影响的理论估算结果,可以得出负重轮动位移均方根值随车辆行驶速度的变化情况,见图 9.

|
图9 第一负重轮动位移均方根值变化情况 Fig. 9 Changes of RSM to dynamic displacement for the first road wheel |
通过图 8和图 9可以得出以下结论:
1) 第一负重轮动位移变化量均方根值随车辆行驶速度呈现不规律变化趋势,行驶速度为50 km/h时第一负重轮动位移的均方根值最大,行驶速度为60 km/h时第一负重轮动位移的均方根值最小.这主要是因为随着车辆行驶速度的提高,负重轮受到的冲击激励增大,从而造成负重轮动位移的增加;而车辆的行驶速度越高,激励作用于负重轮的时间越短,负重轮对激励响应不充分,从而使负重轮动位移减小.
2) 第一负重轮动位移的仿真结果近似服从正态分布,随着车辆行驶速度的变化,其均方根值相对理论估算值明显降低,这说明履带及其张紧力是影响负重轮动位移的的重要因素,由于履带及履带张紧力的存在,使得负重轮在行驶过程中的动位移明显减少,进而表明履带对地面有明显的滤波作用.
3 结 论本文以负重轮动位移为研究对象,采用理论推导和动力学仿真相结合的方法,研究履带车辆行驶速度对负重轮动位移变化规律的影响.研究结果表明,履带车辆以不同的速度行驶时,负重轮动位移的均方根值变化情况较为复杂,且负重轮的动位移近似成正态分布.履带车辆行驶速度与负重轮动位移变化规律的研究为整车道路模拟系统直接对负重轮进行位移激励加载控制提供了技术支持.
| [1] | 丁法乾.履带式装甲车辆悬挂系统动力学[M].北京:国防工业出版社,2004.(Ding Fa-qian.Tracked armored vehicle suspension system dynamics[M].Beijing:National Defense Industry Press,2004.)( 1) 1) |
| [2] | Dhir A,Sankar S.Ride dynamics of high-speed tracked vehicles:simulation with field validation[J].Vehicle System Dynamics,1994,23(1):379-409.( 1) 1) |
| [3] | Auersch L.The excitation of ground vibration by rail traffic:theory of vehicle-track-soil interaction and measurements on high-speed lines[J].Journal of Sound and Vibration,2005,284:103-132.( 1) 1) |
| [4] | Lee H C,Choi J H.Spatial dynamics of multi-body tracked vehicles.Part II:contact forces and simulation results [J].Vehicle System Dynamics,1998,29(1):113-137.( 1) 1) |
| [5] | Rubinstein D,Hitmn R.A detailed multi-body model for dynamic simulation of off-road tracked vehicles[J].Journal of Terramechanics,2004,41(5):163-173.( 1) 1) |
| [6] | Liu Y,Liu G.Modeling of tracked mobile manipulators with consideration of track-terrain and vehicle-manipulator interactions[J].Robotics and Autonomous Systems,2009,57:1065-1074.( 1) 1) |
| [7] | Garnich M R,Grimm T R.Modeling and simulation of a tracked vehicle[M].Las Vegas:ASME,1984:591-600.( 1) 1) |
| [8] | Wheeler P.Tracked vehicle ride dynamics[J].SAE Preprints,1977,330(15):3744-3765.( 1) 1) |
| [9] | Galvin P,Romero A,Dominguez J.Fully three-dimensional analysis of high-speed train tracks soil-structure dynamic interaction[J].Journal of Sound and Vibration,2010,329:5147-516.( 1) 1) |
| [10] | Wong J Y.Development of high-mobility tracked vehicles for over snow operations[J].Journal of Terramechanics,2009,46(4):141-155. ( 1) 1) |
 2016, Vol. 37
2016, Vol. 37
