目前全断面岩石隧道掘进机[1](tunnel boring machine,TBM)已经广泛应用于硬质岩土中的隧道机械自动掘进施工.滚刀破岩效率直接关系到TBM的施工成本,对TBM掘进性能具有决定性影响[2].
岩石在滚刀作用下的破坏方式目前并未产生明确共识.如剪切破岩理论,岩石属裂纹扩展拉伸破坏,以剪切破坏为主同时辅以挤压和张拉破坏;以张拉破坏为主的拉剪综合失效模式,以剪切破坏为主的拉剪综合失效模式等[3].作者结合前人研究,已对TBM 施工时滚刀作用下岩石破碎的效率进行了一定的研究[4],提出在TBM滚刀作用下岩石以剪切破坏和张拉破坏为主,并以岩石破坏时裂纹长度与剪切面在岩石自由表面投影长度及滚刀刀刃宽度间的关系识别岩石破坏方式并计算岩石破碎体积,结合CSM模型计算破岩比能,并通过工程实例计算验证了该方法的有效性,为TBM的设计与施工提供一定参考.
1 CSM模型下的破岩效率评价方法在盘型滚刀工作过程中,刀具所受作用力Ft的各向分力分别为垂向力、滚动力和侧向力[5].由于侧向力Fs较小,因此通常可不考虑侧向力影响.滚刀受力如图 1所示.

|
图 1 滚刀所受各向分力[5] Fig. 1 Individual forces on cutter |
本文采用刀具破岩比能值作为破岩效率评价参数.比能(specific energy,SE)是研究刀具破岩效率的重要指标,采用能量法,将其定义为刀具切削破坏单位体积岩石所消耗的能量[6]:

式中:SE为比能;Fn为滚刀所受垂向力;Fr为滚刀所受滚动力;p为滚刀贯入度;l为滚刀滚动切削行程;V为岩石破碎体积;∑Fn为刀盘所受总垂向力;∑Fn·l为刀盘所受总扭矩.
对于Ft,本文采取应用最为广泛的由科罗拉多矿业学院(Colorado School of Mines,CSM)提出的CSM预测模型[7]进行估算.此模型在数学分析的基础上经大量试验验证,已经在众多工程中得到了成功应用,比其他模型具有更高准确性,该模型不考虑滚刀所受侧向力.
盘形滚刀所受作用力


联立式(2)~式(5),计算Fn和Fr:

将式(6)和式(7)代入到式(1)中,即可求出刀具破岩比能值.
2 岩石破碎体积计算方法 2.1 岩石破坏方式TBM并非要将掌子面处岩石碾压成岩屑,其目的主要为利用滚刀滚压岩石使掌子面表面岩石碎块掉落[8].岩石破碎体积与其破坏方式联系紧密,结合文献[5],对其破坏简化考虑,岩石受滚刀作用形成的受压粉核区较小,滚刀破岩过程主要以岩石剪切破坏和张拉破坏为主,并通过岩石破坏时裂纹长度和剪切面在岩石自由表面投影长度以及滚刀刀刃宽度间的关系来识别其破坏方式.
根据文献[5, 9],岩石在刀具作用下形成压碎破坏区之后产生的侧向裂纹扩展长度L经数值模拟方法拟合得到的计算公式为

岩石存在破碎角β,当剪切破坏面在岩石自由表面投影长度(x)大于L与一半的刀刃宽度(T)之和,即x=ptan >L+
>L+ 时认为岩石以剪切破坏为主;反之则认为岩石以裂纹张拉扩展破坏为主.
时认为岩石以剪切破坏为主;反之则认为岩石以裂纹张拉扩展破坏为主.
本文认为TBM上每把刀的受力情况与破碎岩石情况均相同,岩石破碎体积的计算式为

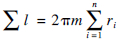 计算.
计算.
通过对5种不同滚刀间距情况进行简化处理(对岩石破坏简化为仅考虑剪切破坏区与裂纹张拉区),得出在每种情况下的岩石破碎体积计算公式,简化结果如图 2所示.图中T为滚刀刀刃宽度,L为侧向裂纹长度,p为滚刀贯入度,认为其近似取剪切面最大深度,β为岩石破碎角,S为滚刀刀刃中心间距,c为相邻滚刀间剪切面交叉区投影长度.经此简化,则可得剪切面在岩石自由表面投影长度为x=ptan .
.

|
图 2 岩石破碎截面 Fig. 2 Section of broken rock (a)—2L+T<2x<S; (b)—2L+T<S<2x; (c)—S<2L+T<2x; (d)—2x<2L+T<S; (e)—2x<2L+T,S<2L+T. |
当x=ptan >L+
>L+ ,且
,且 S≥x=ptan
S≥x=ptan 时,如图 2a所示,此时认为滚刀之间属独立破坏岩石,岩石以剪切破坏为主,则
时,如图 2a所示,此时认为滚刀之间属独立破坏岩石,岩石以剪切破坏为主,则

当x=ptan >L+
>L+ ,L+
,L+ <
< S<x=ptan
S<x=ptan 时,如图 2b所示,经计算可得
时,如图 2b所示,经计算可得 c=ptan
c=ptan -
- S.根据文献[10],由于施工扰动的影响,岩石中的非贯通裂纹可能会发生张开、闭合或扩展,岩桥可能会失稳造成破坏,因此此处引入控制参数(破坏扩大系数)ξ,ξ>1.该情况下,认为滚刀之间属协同破坏岩石,岩石以剪切破坏为主,则
S.根据文献[10],由于施工扰动的影响,岩石中的非贯通裂纹可能会发生张开、闭合或扩展,岩桥可能会失稳造成破坏,因此此处引入控制参数(破坏扩大系数)ξ,ξ>1.该情况下,认为滚刀之间属协同破坏岩石,岩石以剪切破坏为主,则
当x=ptan >L+
>L+ ,且12S≤L+
,且12S≤L+ 时,如图 2c所示,此时滚刀间剪切面有所交叉,且同时侧向裂纹发生交汇贯通.引入控制参数破坏厚度系数λ,当裂纹向岩石深部扩展交汇贯通时λ>1;当裂纹平行于岩石自由表面扩展交汇贯通时λ=1;当裂纹向岩石自由表面扩展交汇贯通时λ<1.该情况下,认为滚刀之间属协同破坏岩石,岩石属于剪切-张拉破坏,以剪切破坏为主,则
时,如图 2c所示,此时滚刀间剪切面有所交叉,且同时侧向裂纹发生交汇贯通.引入控制参数破坏厚度系数λ,当裂纹向岩石深部扩展交汇贯通时λ>1;当裂纹平行于岩石自由表面扩展交汇贯通时λ=1;当裂纹向岩石自由表面扩展交汇贯通时λ<1.该情况下,认为滚刀之间属协同破坏岩石,岩石属于剪切-张拉破坏,以剪切破坏为主,则

当x=ptan >L+
>L+ ,且
,且 S≤L+
S≤L+ 时,仍采取前述简化方式,如图 2d所示,此时刀刃间剪切面与扩展裂纹均无交汇,只有剪切破坏区形成的碎片,岩石内部张拉裂纹由于并未贯通而形成岩脊,其岩石截面破碎面积可视同独立单滚刀破岩情况.该情况下,认为滚刀之间属独立破坏岩石,岩石属于剪切-张拉破坏,且以裂纹张拉扩展破坏为主,则
时,仍采取前述简化方式,如图 2d所示,此时刀刃间剪切面与扩展裂纹均无交汇,只有剪切破坏区形成的碎片,岩石内部张拉裂纹由于并未贯通而形成岩脊,其岩石截面破碎面积可视同独立单滚刀破岩情况.该情况下,认为滚刀之间属独立破坏岩石,岩石属于剪切-张拉破坏,且以裂纹张拉扩展破坏为主,则

当x=ptan >L+
>L+ ,且
,且 S≤L+
S≤L+ 时,如图 2e所示,此时刀刃间侧向扩展裂纹发生交汇贯通,从而使滚刀之间的岩石剥落破坏.该情况下,可认为滚刀之间属于协同破坏岩石,岩石属于剪切-张拉破坏,且以裂纹张拉扩展破坏为主,则
时,如图 2e所示,此时刀刃间侧向扩展裂纹发生交汇贯通,从而使滚刀之间的岩石剥落破坏.该情况下,可认为滚刀之间属于协同破坏岩石,岩石属于剪切-张拉破坏,且以裂纹张拉扩展破坏为主,则

以秦岭隧道工程[11]为例,采用本文提出的计算方法,分别计算了该工程所使用的TBM在刀盘旋转一周时所受的总垂向力、总扭矩和总岩石破碎体积.秦岭隧道的岩石以混合花岗岩和混合片麻岩为主,抗压强度平均在150 MPa左右,抗拉强度在6 MPa左右.
该工程所采用的TB880E型隧道掘进机刀盘直径为8 800 mm,共布置了71把17寸盘型滚刀.分别求出中心滚刀区 =1.512 m,该区刀间距S1平均为84 mm;正面滚刀1区
=1.512 m,该区刀间距S1平均为84 mm;正面滚刀1区 =8.470 m,该区刀间距S2平均为70 mm;正面滚刀2区
=8.470 m,该区刀间距S2平均为70 mm;正面滚刀2区 =103.607 m,该区刀间距S3平均为65 mm;边缘滚刀区
=103.607 m,该区刀间距S3平均为65 mm;边缘滚刀区 =58.303 m,该区刀间距S4平均为45 mm;刀盘总平均刀间距S为65 mm.
=58.303 m,该区刀间距S4平均为45 mm;刀盘总平均刀间距S为65 mm.
本文根据实际地质条件和掘进机刀具布置,计算参数取值如下[10]:
n=71,p=9 mm,R=216 mm,m=1,T=20 mm,ψ=0.1,c=2.12,σc=150 MPa,σt=6 MPa,ξ=1.3,λ=1.0,S=65 mm, =1.512 m,
=1.512 m, =8.470 m,
=8.470 m, =103.607 m,
=103.607 m, =58.303 m,
=58.303 m, =171.892 m.
=171.892 m.
将上述参数代入式(2)~式(5),可以得出单把滚刀所受作用力Ft=186.238 kN,小于滚刀承载能力250 kN,较为合理.通过式(6)、式(7),可以求出单把滚刀所受垂向力Fn=184.288 kN,单把滚刀所受切削力Fr=26.881 kN.由此可得总垂向力∑Fn=n·Fn=13 084.448 kN;总扭矩∑Fr·l=Fr· =4 620.629 kN·m.
=4 620.629 kN·m.
通过式(8)~式(10),可计算出L=7 mm,则x=ptan =51 mm>L+
=51 mm>L+ =17 mm,且0.5S1=42 mm,0.5S2=35 mm,0.5S3=32.5 mm,0.5S4=22.5 mm,则在刀盘上4个滚刀布置区均符合情况L+
=17 mm,且0.5S1=42 mm,0.5S2=35 mm,0.5S3=32.5 mm,0.5S4=22.5 mm,则在刀盘上4个滚刀布置区均符合情况L+ <
< S<x=ptan
S<x=ptan ,利用式(13)计算得到V1=0.006 m3,V2=0.029 m3,V3=0.337 m3,V4=0.150 m3,从而总的岩石破碎体积为V=V1+V2+V3+V4=0.522 m3.
,利用式(13)计算得到V1=0.006 m3,V2=0.029 m3,V3=0.337 m3,V4=0.150 m3,从而总的岩石破碎体积为V=V1+V2+V3+V4=0.522 m3.
由文献[11]分析本文计算结果如表 1所示.
| 表 1 实际值与计算值对比 Table 1 Comparison of actual values and calculated values |
由表 1可知,误差值均小于10%,且计算所得岩石破碎体积较为准确.由此数据结合式(1),即可得到TBM滚刀刀具破岩比能值,从而可以对TBM施工进行预测分析.
4 结论1) 以岩石破坏时裂纹长度与剪切面在岩石自由表面投影长度及滚刀刀刃宽度间的关系识别岩石破坏方式并计算岩石破碎体积的方法有效.
2) 结合CSM模型及本文提出的岩石破碎体积计算方法可以得出破岩比能值,并可据此评估滚刀破岩效率.
3) 破岩比能值反映滚刀破岩效率的大小,破岩比能值越小,滚刀破岩效率越高.
| [1] | Lu Y,Ma J M,Xu Q J,et al.TBM in the future of China[J].Marine Georesources and Geotechnology,2004,22(3):185-193.( 1) 1) |
| [2] | Rostami J,Ozdemir L,Nilson B.Comparison between CSM and NTH hard rock TBM performance prediction models[C]// Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling Technology.Las Vegas,1996:1-10.( 1) 1) |
| [3] | 赵贺兴.TBM滚刀破岩作用机制及其效率评价研究[D].沈阳:东北大学,2015.(Zhao He-xing.Study of rock fragmentation characteristic and efficiency evaluation by TBM disccutters[D].Shenyang:Northeastern University,2015)( 1) 1) |
| [4] | 赵贺兴,王述红,昝世明,等.基于不同岩石破坏方式的滚刀效率评价模型研究[J].水利与建筑工程学报,2015(4):6-11.(Zhao He-xing,Wang Shu-hong,Zan Shi-ming,et al.Model study on the efficiency evaluation of TBM disc cutters based on different kinds of rock fragmentation methods[J].Journal of Water Resources and Architectural Engineering,2015(4):6-11.)( 1) 1) |
| [5] | 朱逸.TBM多滚刀组合破岩特性的数值模拟及实验研究[D].长沙:中南大学,2013.(Zhu Yi.Numerical simulation and experimental study of rock fragmentation characteristic by TBM disc cutters[D].Changsha:Central South University,2013.)( 4) 4) |
| [6] | Acaroglu O,Ozdemir L,Asbury B.A fuzzy logic model to predict specific energy requirement for TBM performance prediction[J].Tunneling and Underground Space Technology,2008,23(5):600-608.( 1) 1) |
| [7] | Ozdemir L.Development of theoretical equations for predicting tunnel boreability[D].Golden:Colorado School of Mines,1977.( 1) 1) |
| [8] | Cho J W,Jeon S,Yu S H,et al.Optimum spacing of TBM disc cutters:a numerical simulation using the three-dimensional dynamic fracturing method[J].Tunneling and Underground Space Technology,2010,25(3):230-244.( 1) 1) |
| [9] | Liu H Y,Kou S Q,Lindqvist P A.Numerical studies on bit-rock fragmentation mechanisms[J].International Journal of Geomechanics,2008,8(1):45-67.( 1) 1) |
| [10] | 郭牡丹,朱浮声,王述红,等.岩体非贯通结构面的岩桥贯通准则研究[J].岩土工程学报,2013,35(8):1513-1518.(Guo Mu-dan,Zhu Fu-sheng,Wang Shu-hong,et al.Coalescence criterion for ligament of rock mass containing discontinuous structural planes[J].Chinese Journal of Geotechnical Engineering,2013,35(8):1513-1518.)( 2) 2) |
| [11] | 张厚美.TBM的掘进性能数值仿真研究[J].隧道建设,2007,26(02):1-7.(Zhang Hou-mei.Study on numerical simulation of performance of tunnel boring machines (TBM)[J].Tunnel Construction,2007,26(02):1-7.)( 3) 3) |
 2016, Vol. 37
2016, Vol. 37
