有将近一半的脊椎骨折发生在T11-L2节段中.虽然爆裂骨折在其中的占比为15%, 但是爆裂骨折引起的神经损伤率却高达60%.爆裂骨折的表现为发生骨折的椎骨节段, 其部分骨折碎片侵入到椎管中, 造成椎管狭小, 引起神经损伤.垂直方向的高能量冲击力是引起爆裂骨折的最重要原因, 常见于生活中的事例就是高空坠落和车祸.
Holdsworth[1]首先提出了爆裂骨折定义, 并将脊椎定义为两柱体来解释爆裂骨折.Denis[2]在此基础上定义了更细分的三柱体来解释爆裂骨折.Kifune等[3]利用一个高塔释放重物的设备冲击胸腰椎节段来再现爆裂骨折的发生, 以研究在不同的冲击能量下, 爆裂骨折的发生率.Isomi等[4]研究在爆裂骨折后, 人体在前屈和后伸姿势时, 椎管的横截面面积变化.El-Rich等[5]建立一个L4-L5节段的腰椎模型并赋予失效材料来研究在不同的载荷速率下腰椎发生骨折的具体过程.王吉博[6]建立了T10-L2节段的有限元模型来模拟爆裂骨折后的两种治疗方案效果.文献[7]统计了各种不同的骨折类型并加以分类, 归纳总结了诱发不同骨折类型的作用力的形式.
本文的目的是研究人体脊椎胸腰节段在直立、前屈和后伸三种姿势下爆裂骨折的发生机制, 提取评估爆裂骨折的相关参数, 分析三种姿势下爆裂骨折的严重程度, 为爆裂骨折的研究提供一个新的思路和方法.
1 材料和方法 1.1 T12-L2胸腰椎模型的建立本模型是以一个处于50百分位的成年中国女性仰卧的脊椎CT断层图片为基础重建的几何模型.CT图像厚度为0.6 mm, T12-L2节段的CT图像为374张, 然后导入到MIMICS软件中获得胸腰节段的3D几何外形, 再导入到处理几何软件ANSA中进行有限元网格的划分, 最后导入到hypermesh中进行材料属性的赋予、边界条件的加载等, 利用内置的RADIOSS求解器进行计算分析.
椎体可分为皮质骨和松质骨.为了得到更准确的结果, 根据文献[8]的研究, 本模型将皮质骨和终板划分为9个不同厚度的3节点三角形网格区域, 将松质骨划分为7个不同材料属性的4节点四面体网格区域, 如图 1所示.

|
图 1 皮质骨和松质骨的不同材料属性区域示意图 Fig.1 Schematic diagram of different material property regions of cortical bone and cancellous bone |
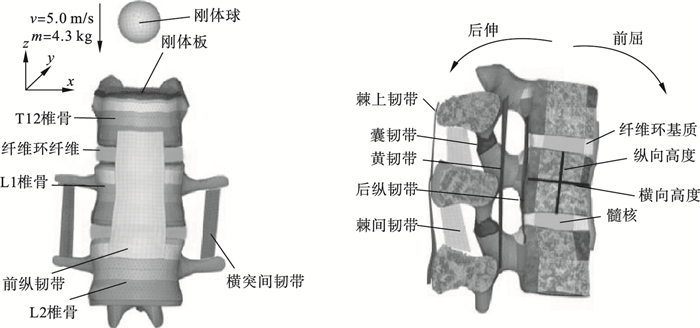
椎间盘建立在相邻上下终板间, 椎间盘被划分为两个部分, 分别为纤维环和髓核, 所占体积分别约为56%和44%.纤维环被划分为纤维环基质和纤维环纤维两部分, 其中, 纤维环纤维的体积约为基质的19%.椎间盘在纵向被划分为7层结构, 纤维环基质在周向被划分为6层结构, 纤维环纤维为3D-truss单元包裹基质, 与上下终板的角度约为±35°.胸腰椎段共有7个韧带结构, 分别为前纵韧带、后纵韧带、黄韧带、棘间韧带、棘上韧带、横突间韧带、囊韧带.所有韧带都以1 mm厚度的面单元组成, 除了囊韧带为3节点三角形单元外, 其余韧带都是4节点四边形单元,如图 2所示.
|
图 2 T12-L2节段有限元模型 Fig.2 Finite element model of T12-L2 |
骨骼的材料属性与弹塑性材料存在类似的变形及屈服极限点, 在屈服极限点以前, 骨头的属性为弹性材料, 在超过屈服点之后, 材料的属性为塑性变形.因此使用Johnson-Cook弹塑性材料公式来模拟骨骼的材料性质, 并加入失效条件来模拟骨骼的断裂.在标准温度下, 塑性应力的等效公式为

|
(1) |

|
(2) |
式中:σ为等效应力;A为屈服应力;B为硬化模量;n为硬化指数;C为应变率系数;εp为塑性应变;

| 表 1 椎骨的材料属性 Table 1 Material properties of vertebral bone |
| 表 2 材料参数的失效验证结果 Table 2 Validation of material properties in failure |
纤维环和髓核采用了带有应变能密度公式的一阶不可压缩Mooney-Rivlin超弹性公式:

|
(3) |
式中:C10, C01为材料常数;I1, I2为变形张量的不变量;W为能量密度.
Mooney-Rivlin超弹性公式没有考虑到应变率的影响, 但实验结果表明, 应变率对椎间盘的材料属性有很大的影响, 因此将材料属性分为低速和高速材料, 如表 3所示.其中低速材料应用于静态或准静态分析, 如本文中模型的验证是在准静态条件下模拟的, 采用低速率材料属性.碰撞是在高应变率的动态条件下模拟的, 选用高速率材料属性.纤维环纤维和韧带的材料属性采用文献[10]的数据.
| 表 3 椎间盘的材料属性 Table 3 Material properties of intervertebral disc |
仿真的坐标轴系如图 2所示, 竖直向上为z轴的正方向, y轴方向为从左到右, x轴方向为从前到后.L2下表面和后部结构的所有自由度都被固定.
为了将冲击力均匀同时地传递到椎骨上, 在T12上方建立1个以T12上表面外形为基础, 厚度为3 mm的刚体板并与T12绑定连接.撞击脊椎的刚体球忽略重力加速度, 给予1个竖直向下的5 m/s初速度, 刚体球半径为11 mm, 质量为4.3 kg, 刚体球最低点距离刚体板上表面20 mm, 刚体球的中心与T12中心处于1条竖直直线上.
本文模拟3种姿势下的爆裂骨折结果, 3个模拟过程分别为直立姿势、前屈姿势和后伸姿势.直立姿势就是模型建立时的姿势, 前屈姿势和后伸姿势需要将脊椎模型弯曲一定角度.结合脊椎的生理活动曲线, 保证撞击前模型的完整性, 根据文献统计的人体脊椎各节段的活动范围[11], 本文在T12上表面施加了使脊椎前屈和后伸弯曲8°的力矩, 仿真持续总时间为6 ms.为了使计算步长在合理范围, 节约计算时间和得到易收敛的结果, 在撞击前的0~4 ms, 将8°的弯曲力矩线性增长地施加到T12上, 在4 ms后保持8°直到仿真结束.为了保证在刚体球撞击椎体时与T12中心仍处于同一竖直直线上, 在前屈后伸姿势时, 刚体球应在仿真开始前调整到相应的位置.
椎间盘和韧带与椎骨的连接方式为绑定接触, 相邻的关节突、刚体球与刚体板及所有的不同结构的部件之间都采用了无摩擦的接触方式以防止可能的穿透.
1.4 模型验证为了保证结果的准确性, 需要对模型进行验证.将T12-L2模型分成T12-L1和L1-L2两段分别验证.T12-L1在前后弯曲、左右侧弯、轴向左右弯曲6个方向上施加7.5 N·m线性增加的力矩.L1-L2在同样的6个方向上施加包含100 N预应力的10 N·m线性增加的力矩.
2 结果 2.1 模型验证结果T12-L1, L1-L2节段模型的验证结果如图 3所示, 与已发表的参考文献结果[12-13]相比, 在误差允许的范围内高度吻合, 变化趋势也非常相近, 因此, 模型的验证结果是准确的, 可以进行模拟分析.

|
图 3 模型的验证结果 Fig.3 Model validation results (a)~(c)—T12-L1节段;(d)~(f)—L1-L2节段. |
3种模拟条件下刚体球撞击模型产生的最大接触力为(11±0.8) kN, 因此, 可以认为3种模拟为相同能量冲击下的对比.在3种模拟仿真中, 破坏的位置都发生在L1椎体.在前屈姿势下, 由于L1上端骨折分离出的楔形碎片变形太大, 因此, 在前屈姿势下, 模拟在5.7 ms停止.
在直立状态时, 骨折破坏开始于椎体上半部分的后壁处及两侧的椎弓根与终板的邻近区域, 随后骨折向椎体中心和前部延伸, 在骨折延伸过程中, 椎体下半部分前端在矢状面上裂开.在后伸姿势时, 骨折的破坏过程与直立状态时相似, 但椎体下半部分保持完整.在前屈姿势下, 骨折开始于椎体上半部分的中间前壁靠近终板的位置, 随后破坏向终板中心延伸.3种姿势在4个时间点:4.5, 5.0, 5.5, 6.0 ms(前屈状态5.7 ms)的应力云图如图 4所示.

|
图 4 不同姿势下松质骨在4个时间节点的应力云图 Fig.4 Stress distribution of trabecular bone in different postures at four time points (a)—直立姿势;(b)—后伸姿势;(c)—前屈姿势. |
3种姿势下椎体L1的纵向高度减少、横向宽度增加, T12-L1关节突接触力的时间曲线如图 5~7所示.在图 5中, 前屈姿势高度丢失最大, 为4.12 mm, 后伸姿势为3.64 mm, 直立姿势最小, 为3.19 mm.在图 6中, 后伸姿势横向宽度增加7.32 mm, 向椎管内偏移量最大;直立姿势横向宽度增加2.33 mm;在前屈姿势下, 横向宽度基本没有变化.在图 7中, 后伸姿势得到最大的接触力为0.36 kN, 直立姿势下的最大接触力为0.136 kN, 前屈姿势下的最大接触力为0.09 kN.

|
图 5 纵向高度减少位移曲线 Fig.5 Displacement curves of longitudinal height reducation |

|
图 6 横向宽度增加位移曲线 Fig.6 Displacement curves of lateral widthincreasement |

|
图 7 关节突接触力曲线 Fig.7 Contact force curves of facet joints |
3种姿势下的最终骨折形式如图 8所示(隐藏部分失效单元), 其相应的骨折类型都可在文献[7]中找到对应的分类.

|
图 8 仿真骨折结果与Magerl的分类对比图 Fig.8 Comparison of simulation fractures to Magerl's classification |
本文使用了一个具有破坏准则的胸腰椎节段模型来研究在3种不同姿势下该节段的爆裂骨折原理.这个方法不仅再现了脊椎爆裂骨折的过程, 还对比了3种不同姿势下爆裂骨折的差异, 并且将得到的3种骨折类型与文献进行对比分析, 保证了其骨折形式的合理性.碰撞产生的骨折更符合实际情况.在韧带结构中, 压缩力为主要作用力时, 很少发生破坏[2], 因此本模型没有将韧带结构的破坏准则加入.根据文献[14]可知, 产生椎体破坏的冲击能量为50~180 J, 本文的冲击能量为56 J, 在此区间内.
临床观测CT图和实验室碰撞结果如图 9所示[15-16].图 9a的结果与本次模拟前屈状态下的碰撞结果相似, 椎体前柱完全破坏, 椎体高度严重损失.图 9b的CT图表明椎骨的上终板完全破坏, 从上终板到椎体前柱, 部分椎体形成楔形碎片, 脊椎后柱侵入到脊椎管当中, 造成椎管狭窄, 这与本次模拟后伸姿势下的碰撞结果相似.图 9c是实验室中T12-L2节段垂直碰撞的结果, 其终板完全破坏, 且在椎骨前部结构中, 有楔形的骨头碎片形成, 这与本文直立姿势的模拟仿真结果非常相似.

|
图 9 临床CT观测图和实验室碰撞结果图 Fig.9 CT images in clinic observation and collision result in experiment (a)—与前屈姿势骨折相似的CT扫描图;(b)—与后伸姿势骨折相似的CT扫描图;(c)—与直立姿势骨折相似的实验室碰撞结果. |
文献[7]统计了大量的骨折类型并描述了相应作用力形式.爆裂骨折的最主要作用力就是垂直向下的压缩力, 这与本文的垂直冲击力相吻合.不同力造成不同骨折类型的原因:①脊椎在受到垂直载荷作用前有预加载时, 其椎间盘产生了不同方向的剪切力;②关节突在不同的预加载条件下, 在受到垂直载荷时传递的接触力是不同的.
纵向高度减少被用来评估椎体的骨折严重程度, 横向宽度增加则与椎管狭窄相关, 是爆裂骨折的重要评价参数.关节突是脊椎重要的维持稳定的结构, 也是评价椎管狭窄的参数, 因此, 关节突接触力在爆裂骨折的形成中也有重要作用.在图 5~7中, 前屈姿势的纵向高度减少最大, 与后伸姿势与直立姿势相比增加了约12%和29%;而在横向宽度参数上, 前屈姿势下基本没有变化, 后壁的完整也间接表明了这点;关节突接触力上也是最小值.而后伸姿势在横向宽度增加和关节突接触力中的值都是最大的, 即造成的椎管狭窄程度最严重, 也最有可能引发严重的神经损伤.
4 结语本文通过建立一个完整的胸腰椎节段T12-L2, 利用失效准则模型研究直立、前屈、后伸3种姿势下爆裂骨折的原理机制, 得到了3个在临床观测中分类的骨折类型, 为爆裂骨折的研究提供了一个新的方法和思路.在这3种姿势中, 后伸姿势下爆裂骨折的程度更严重.
| [1] |
Holdsworth F. Fractures, dislocations, and fracture-dislocations of the spine[J]. Journal of Bone & Joint Surgery, 1970, 52(8): 1534-1551. |
| [2] |
Denis F. The three column spine and its significance in the classification of acute thoracolumbar spinal injuries[J]. Spine, 1983, 8(8): 817-831. DOI:10.1097/00007632-198311000-00003 |
| [3] |
Kifune M, Panjabi M M, Liu W, et al. Functional morphology of the spinal canal after endplate, wedge, and burst fractures[J]. Journal of Spinal Disorders, 1997, 10(6): 457-466. |
| [4] |
Isomi T, Panjabi M M, Kato Y, et al. Radiographic parameters for evaluating the neurological spaces in experimental thoracolumbar burst fractures[J]. Journal of Spinal Disorders, 2000, 13(5): 404-411. DOI:10.1097/00002517-200010000-00006 |
| [5] |
El-Rich M, Arnoux P J, Wagnac E, et al. Finite element investigation of the loading rate effect on the spinal load-sharing changes under impact conditions[J]. Journal of Biomechanics, 2009, 42(9): 1252-1262. DOI:10.1016/j.jbiomech.2009.03.036 |
| [6] |
王吉博. 有限元法评估经皮椎体成形和后凸成形治疗脊柱三明治骨折的生物力学变化[J]. 中国组织工程研究, 2017, 21(35): 5703-5708. (Wang Ji-bo. Biomechanical characteristics of percutaneous kyphoplasty versus percutaneous vertebroplasty for spinal sandwich fracture by finite element analysis[J]. Chinese Journal of Tissue Engineering Research, 2017, 21(35): 5703-5708. DOI:10.3969/j.issn.2095-4344.2017.35.021) |
| [7] |
Magerl F, Aebi M, Gertzbein S D, et al. A comprehensive classification of thoracic and lumbar injuries[J]. European Spine Journal, 1994, 3(4): 184-201. DOI:10.1007/BF02221591 |
| [8] |
Zhao F D, Pollintine P, Hole B D, et al. Vertebral fractures usually affect the cranial endplate because it is thinner and supported by less-dense trabecular bone[J]. Bone, 2009, 44(2): 372-379. DOI:10.1016/j.bone.2008.10.048 |
| [9] |
Garo A, Arnoux P J, Wagnac E, et al. Calibration of the mechanical properties in a finite element model of a lumbar vertebra under dynamic compression up to failure[J]. Medical & Biological Engineering & Computting, 2011, 49(12): 1371-1379. |
| [10] |
Shirazi-Adl A, Ahmed A M, Shrivastava S C. Mechanical response of a lumbar motion segment in axial torque alone and combined with compression[J]. Spine, 1986, 11(9): 914-927. DOI:10.1097/00007632-198611000-00012 |
| [11] |
Wilke H J, Krischak S, Claes L. Biomechanical comparison of calf and human spines[J]. Journal of Orthopaedic Research, 2010, 14(3): 500-503. |
| [12] |
Qiu T X, Tan K W, Lee V S, et al. Investigation of thoracolumbar T12-L1 burst fracture mechanism using finite element method[J]. Medical Engineering & Physics, 2006, 28(7): 656-564. |
| [13] |
Moramarco V, Perez d P A C, Doblare M. An accurate validation of a computational model of a human lumbosacral segment[J]. Journal of Biomechanics, 2010, 43(2): 334-342. DOI:10.1016/j.jbiomech.2009.07.042 |
| [14] |
Germaneau A, Vendeuvre T, Saget M, et al. Development of an experimental model of burst fracture with damage characterization of the vertebral bodies under dynamic conditions[J]. Clinical Biomechanics, 2017, 49: 139-144. DOI:10.1016/j.clinbiomech.2017.09.007 |
| [15] |
陈晓晖, 靳激扬, 何仕诚. 脊椎胸腰段爆裂骨折的CT评估[J]. 现代医学, 2008, 36(5): 349-352. (Chen Xiao-hui, Jin Ji-yang, He Si-cheng. CT evaluation of thoracolumbar burst fracture[J]. Morden Medical Journal, 2008, 36(5): 349-352.) |
| [16] |
Wilcox R K, Allen D J, Hall R M, et al. A dynnamic investigation of the burst fracture process using a combined experimental and finite element approach[J]. European Spine Journal, 2004, 13(6): 481-488. DOI:10.1007/s00586-003-0625-9 |
 2020, Vol. 41
2020, Vol. 41
