东北大学学报:自然科学版   2015, Vol. 36 Issue (2): 288-291   PDF (308 KB)    
引用本文
王海英, 丁华, 张翠华, 王琳. 具有能力约束的供应链系统模型[J]. 东北大学学报:自然科学版 , 2015, 36(4): 288-291.  
WANG Hai-ying, DING Hua, ZHANG Cui-hua, WANG Lin. Combined Model in Supply Chain with Capacity Constraint[J]. Journal Of Northeastern University Nature Science, 2015, 36(4): 288-291.  
具有能力约束的供应链系统模型
王海英1, 丁华2, 张翠华1, 王琳3    
1. 东北大学 工商管理学院， 辽宁 沈阳 110819；
2.沈阳化工大学 经济与管理学院， 辽宁 沈阳 110142；
3.仁川国立大学 社会科学院， 韩国 仁川 406-772
收稿日期：2014-01-10
基金项目：国家自然科学基金青年基金资助项目(71001021,71371043).
作者简介：王海英(1979-)，女，辽宁新民人，东北大学讲师，博士； 张翠华(1971-)，女，辽宁沈阳人，东北大学教授，博士生导师.
摘要：针对包含一个供应商、一个制造商和一个经销商的三级供应链系统进行研究，并依次将系统中的成员称之为首级、中间级和尾级.在相关文献研究的首级和尾级具有能力约束的供应链系统联合批量模型的基础上，建立了一个中间级具有能力约束的三级供应链系统的联合批量模型，并提出了基于推拉混合规则的新的动态规划算法，可在多项式时间求解供应链系统中各个层级的最优决策批量，并通过相关定理的证明保证了算法能够求得全局最优解.最后通过算例分析对上述方法进行了阐述.
关键词： 联合批量     能力约束     供应链     动态规划    
Combined Model in Supply Chain with Capacity Constraint
WANG Hai-ying1, DING Hua2, ZHANG Cui-hua1 , WANG Lin3    
1.School of Business Administration, Northeastern University, Shenyang 110819, China;
2. School of Economics and Management, Shenyang University of Chemical Technology, Shenyang 110142, China;
3. College of Social Sciences， Incheon National University, Incheon 406-772, Korea.
Corresponding author: WANG Lin, E-mail: wanglin@incheon.ac.kr
Abstract: A three-level supply chain composed of a supplier, a manufacturer and a distributor was considered, and the three members of the system are respectively called as first echelon, middle echelon and last echelon. Based on the existing supply chain model where the first and last echelons have capacity constraints, a new integrated lot-sizing model for the three-level supply chain was presented in which the middle echelon has capacity constraints. A new dynamic planning algorithm based on the mixed pull-push rules was proposed to determine the optimal material ordering batches in polynomial time. Some proven theorems show that the global optimal solution should be achieved. The proposed algorithm was explained via solving a simple problem.
Key words: integrated lot-sizing     capacity constraint     supply chain     dynamic programming    


在企业的实际运营过程中，对供应链系统内各成员变量进行统一决策，使得系统实现整体最优[1, 2, 3].在相关文献中，供应链整体决策的问题涉及到能力约束的情况是非常复杂的，Florian 等[4]描述了包含能力约束情况的相关批量问题的求解复杂性.很多文献针对NP－hard类的联合批量问题研究了如何应用启发式算法进行求解[5, 6]，本文对基于具有凹函数形式的目标函数且具有常数能力约束的批量问题展开研究，提出新的多项式时间算法进行求解.

Lee等[7]研究了一个由生产和运输组成的两级供应链系统，其中的运输过程的约束形式为阶跃形式的函数.Kaminsky等[8]讨论了首级和尾级都具有能力约束的三级供应链系统，由于成本函数具有特殊的结构(非投机模式)，三级的供应链系统转化为只有首级具有能力约束的两级供应链系统，并采用了计算复杂度为O(T8)的网络规划算法求解.van Hoesel等[9]对第一级成员具有生产能力约束且目标函数为一般形式的多级供应链系统联合批量决策进行了研究，扩展了前述只有两级的供应链系统的研究，提出了由供应商、多个中间制造商或分销商,以及最终消费者所组成的多级结构模型.

中间级具有能力约束的供应链系统结构不同于首级和尾级具有能力约束的系统，上下级受到资源约束的影响程度完全不同.本文基于对供应链系统结构属性的分析，设计一个新的基于推拉混合求解规则的搜索方法，对中间级具有能力约束的联合批量问题进行求解.

1 模 型

供应链系统是由原材料供应商、生产制造商和下级经销商组成的三级系统.其中制造过程具有常数生产能力约束.文中做出如下基本假设：

①整个生产过程不允许缺货；

②经销商的需求是时变确定性需求；

③生产成本和运输成本为凹函数；

④提前期为零.

在模型建立之前先定义一些基本符号：
n—整个生产过程所包含的周期总数；
j—系统中所处的级数，j=1,2,3；
htj— 供应链系统中第j级在第t期的单位库存持有成本；
t—所处的周期，t =1,2,…,n；
dt—第t期的外部客户需求；
xt—第t期原材料定购数量；
yt—第t期的生产批量；
zt—第t期的运输批量；
Itj—供应链系统的第j级在第t期初的库存量；
ft—第t期原材料补货的固定成本；
C—各个时期的最大生产批量值.

分别用pt，St代表第t期的生产成本和运输成本，Htj代表第j级第t期的库存成本，供应链系统的总成本函数为

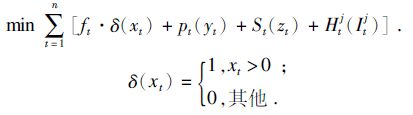
约束条件：

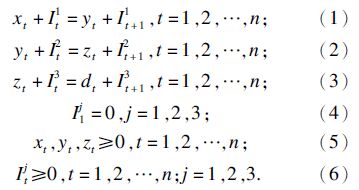
约束条件(1)，(2)，(3)是平衡方程；约束条件(4)表示每个成员的初始库存为零.从目标函数形式可见，目标函数是凹函数.决策变量为各个成员不同时期的原材料订货量、生产量和运输量.

2 定义和定理

2.1 定义

定义1 约束级是指具有能力约束的层级，该层级中的批量值受到能力约束的限制.

定义2 直接约束级是指自身没有能力约束但位于系统中约束级的下游，这类级中的批量值在一定程度上受约束级直接影响.

定义3 间接约束级是指自身没有能力约束但位于系统中约束级的上游，这类层级的批量值在算法上不受约束级的直接影响，但由于取值范围的受限等而受到间接影响.

定义4 一个子计划[u1,u2,v1,v2]，是由生产阶段的时间点(u1,u2)和运输阶段的时间点(v1,v2)所组成的两阶段系统的子集合，其中1≤u1≤ v1≤u2≤v2≤n，且满足Iu12=Iu2－12=Iv13=Iv2－13= 0.

子计划的意义为生产开始于u1点终止于u2点，经过运输过程，正好满足了点v1至点v2之间的需求.

2.2 最优解相关定理

定理1 每个子计划内变量的极值解可以独立确定.

证明 由子计划的定义可知，能够建立子计划的时间点集合之间是独立的.所以，子计划内的变量值是根据自身特征确定的，与其他的子计划没有关系.

定理2 构建由约束级和间接约束级组成的系统的子计划，只要间接约束级的批量流出大于约束级的需求，约束级的极值解可以不受间接约束级限制.

证明 设系统的总计划周期数为n，间接约束级的决策变量为x1,…,xn，成本函数为w(x1,…,xn)，约束级的决策变量为y1,…,yn,成本函数为s(y1,…,yn).给定任意一个可行解(1,1)-(a,b)-(u,v)-(n+1,n+1)，目标函数为min{ w(x1,…,xn) +s(y1,…,ya-1)+ s(ya,…,yu-1) + s(yu,…,yn)}.由定理1可知，各个子计划彼此的解是独立确定的.据此，针对子计划[a,b,u,v]，函数min{ w(x1,…,xn) + s(ya,…,yu-1) }以及min{ w(x1,…,xn) + s(y1,…,ya-1)+ s(ya,…,yu-1) + s(yu,…,yn)}的最优解是相同的.针对min{ w(x1,…,xn) + s(ya,…,yu-1) }，如果xt+It≥yt，说明间接约束级满足约束级的需求.设存在xt′，也满足xt′+It≥yt， 那么min{ w(x1′,…,xn′) + s(ya,…,yu-1) }和min{ w(x1,…,xn) + s(ya,…,yu-1) }是否会具有关于y的相同的极值解？显然，对于这两个函数，w(x1,…,xn)与w(x1′,…,xn′)只是两个值不同的常数，并不影响关于约束级决策变量的极值解.

推论 一个中间级具有能力约束的三级供应链系统，成员包括间接约束级、约束级和直接约束级，对于任意可行解中的子计划，直接约束级的极值解取值不受间接约束级的影响.

2.3 推拉混合运算规则的建立

根据上述的定理和推论，针对中间级具有能力约束的多级供应链系统建立新的计算规则，称之为推拉混合规则：对于供应链系统中直接约束级和约束级构建供应链子系统，先在子系统内构建可行子计划，采用推式规则确定该部分子计划的极值解；对供应链系统总体构建子计划，采用拉式规则寻找全局可行解并确定相对应的间接约束级极值解；最后确定全局最优解.

3 求解最优解的算法步骤

3.1 构建子系统的子计划

对于所有满足u1≤ v1≤u2≤ v2的时间点采用网络图法构建子计划[u1,u2, v1,v2],包括产生可行点以及在可行点之间产生可行弧.

1) 产生可行点：可行点(u,v)表明始于u点的生产批量满足始于v点的需求量，其中1≤u≤v≤n+1.

2) 产生可行弧：在任意两点(u1,v1) 和 (u2,v2) 之间可能存在一个弧(u1<u2，v1<v2)，含义为u1+1和u2之间的生产量，恰好满足v1+1和v2之间的需求量，即构成子计划[u1,u2,v1,v2].

可行弧筛选方法:

a.对于终点(u2,v2)，若u1(u1< u2)的值一定，那么v1的值必须满足公式≤.其含义是，u1和u2之间最大生产量要大于v1和v2之间需求总量，否则为不可行弧.

b.对于点(u2,v2)，若其和点(u3,v3)之间已经不存在可行弧(u3>u2且u3≤ v3≤n+1)，可知点(u1,v1)和点(u2,v2)之间也可能存在可行弧(u1<u2 且 u2≤ v2≤ n+1).

c.给定点(u1,v1)，如果在点(1,u1-1)之间最大生产量总和小于(1,v1-1)之间总需求，那么点(u1,v1)和任一点(u2,v2) (u1<u2)之间不存在可行弧.

3.2 子计划成本计算

1) 选取状态变量.

选取生产和运输过程的库存水平(It2,It3).当t= u1+1，或u2+1≤t ≤ v2+1时，状态变量为It2＝0；当u1+1≤t ≤ u2+1，或者t= v2+1时，It3＝0.

2) 决策变量的确定.

子系统的决策变量为生产批量和运输批量，二者为联合决策变量(yt,zt).

3) 状态转换方程.

状态转换方程即库存平衡方程式(7)和式(8):

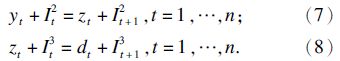
4) 动态规划方程的建立.

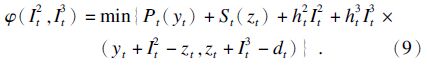
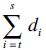式中：yt∈(0,b,C);zt=yt+It2 或者 zt = －It3，t≤s≤m2.

3.3 构建全局可行解

针对供应链全系统构建全局可行解，在网络图中逐步寻找可行弧组成的所有可行解.全局可行解的数目最大值为E=2×3×…×(n-1)=(n-2)( n+1)/2.

全局可行解内变量值的确定：变量xt的确定方法为将yt*作为已知数，建立全局的动态规划方程，其中状态变量为It1.

用G(It1)代表原材料补货成本.其中第k个可行解的动态规划方程为

式中：xt≥0;It1+xt≥yt*;1≤k≤E.

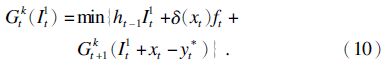
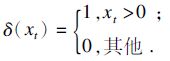
当t=n，有Gn k(In1)=min{hn－1In1+δ(xn)fn}.式中：xn≥0;In1+xn=yn*.

3.4 计算总成本

用F(u, v)代表为满足在期间u+1,…,n(0≤u≤n)的客户需求，在v+1,…,n (0≤v≤n)期间进行生产所产生的最小成本值.第k个可行解总成本为 TCk=Fk(0,0)+G0k(0),1≤k≤E.最低总成本为TC*=min {TC k，1≤k≤E }.

4 算例分析

假设n＝5，t=1,2,3,4,5.各个时期的需求分别为(1,2,1,3,4).各个成员的单位库存成本分别为0.5，1.2，1.5，原材料补货成本ft＝1，生产能力约束C＝3；

生产函数和运输函数分别为

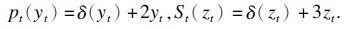
具体计算过程如下.

1) 生成子计划：共生成8个子计划，分别为(1,2,1,2)，(2,3,2,3)，(1,2,1,3)，(1,3,1,3)，(3,6,3,6)，(2,6,3,6)，(2,6,2,6)，(1,6,1,6).

2) 计算子计划成本：子计划的成本和相应的决策变量值y和z.对应子计划分别为[-1,-1,2],[-2,-2,4],[(3,0),(1,2),8][(3,0) (1,2),8],[(2,3,3),(1,3,4),18],[(2,3,3),(1,3,4),18],[(3,1,3,3),(2,1,3,4),23],[(2,3,0,3,3),(1,2,1,3,4),27].

3) 生成全局可行解：根据子计划可组成5个全局可行解，每个可行解和相应的变量值和成本见表 1.

表1 可行解及相应的成本值及决策变量值 Table 1 Feasible solutions and the corresponding costs and variables

4) 得出全局最优解：最后的最低总成本为18.9，各个成员最优的补货数量见表 1.

5 结 论

本文研究了中间级具有常数能力约束的供应链系统联合批量问题.根据供应链系统中能力约束所在的层级，给出了约束级、直接约束级和间接约束级的定义，同时分析了不同级之间的制约关系.可在多项式时间O(n7)求解出供应链系统中各个层级的最优决策批量，并通过相关定理的证明保证了算法能够求得全局最优解.最后进行了算例分析.

参考文献
[1] Onur K,Deniz K,Lerzan O.A coordinated production and shipment model in a supply chain[J].International Journal of Production Economics,2013,143(1):120-132.(1)
[2] Fu B,Huo Y M,Zhao H R.Coordinated scheduling of production and delivery with production window and delivery capacity constraints[J].Theoretical Computer Science,2012,422:39-51.(1)
[3] Thomas D J,Griffin P M.Coordinated supply chain management[J].European Journal of Operational Research,1996,94(1):1-15.(1)
[4] Florian M,Lenstra J K,Rinnooy Kan A H G.Deterministic production planning:algorithms and complexity[J].Management Science,1980,26(7):669-679.(1)
[5] Salomon M,Kuik R,van Wassenhove L N.Statistical search methods for lot sizing problems[J].Annals of Operations Research,1993,41(4):453-468.(1)
[6] Xie J,Dong J.Heuristic genetic algorithms for general capacitated lot-sizing problems[J].Computers and Mathematics with Applications,2002,44(1/2):263-276.(1)
[7] Lee C Y,Cetinkaya S,Jaruphongsa W.A dynamic model for inventory lot sizing and outbound shipment scheduling at a third-party warehouse[J].Operations Research,2003,51(5):735-747.(1)
[8] Kaminsky P,Simchi-Levi D.Production and distribution lot sizing in a two stage supply chain[J].IIE Transactions,2003,35(11):1065-1075.(1)
[9] van Hoesel S,Romeijn H E,Morales D R,et al.Integrated lot sizing in serial supply chains with production capacities[J].Management Science,2005,51(11):1706-1719.(1)