乘积空间中凹泛函型锥拉伸与压缩不动点定理

引用本文

张国伟, 张秀萍. 乘积空间中凹泛函型锥拉伸与压缩不动点定理[J]. 东北大学学报:自然科学版 , 2015, 36(4): 301-304. 复制到剪切板

ZHANG Guo-wei, ZHANG Xiu-ping. Fixed Point Theorems of Cone Expansion and Compression of Concave Functional Type in Product Space[J]. Journal Of Northeastern University Nature Science, 2015, 36(4): 301-304. 复制到剪切板

乘积空间中凹泛函型锥拉伸与压缩不动点定理

张国伟, 张秀萍

东北大学理学院，辽宁沈阳 110819

收稿日期：2013-11-29

基金项目：辽宁省自然科学基金资助项目(201102070).

作者简介：张国伟(1965-),男,辽宁沈阳人,东北大学教授.

摘要：考虑赋范线性空间的乘积空间, 由因子空间中的锥生成乘积空间中的锥. 全连续算子定义在乘积空间中锥与两个闭球相交得到的有界闭集上, 并且值域在锥中. 在由锥上一类非负正齐次凹泛函表示的混合型锥拉伸与压缩条件下, 利用构造性方法将其转化为Schauder型问题, 证明了几个全连续算子的不动点定理. 通过例子说明这里所需要的凹泛函在常用的空间及其锥上是容易构造的.

关键词：不动点全连续算子锥拉伸与压缩凹泛函乘积空间

Fixed Point Theorems of Cone Expansion and Compression of Concave Functional Type in Product Space

ZHANG Guo-wei , ZHANG Xiu-ping

School of Sciences, Northeastern University, Shenyang 110819, China.
Corresponding author: ZHANG Guo-wei, professor, E-mail: gwzhangneum@sina.com

Abstract: A product space of normed linear spaces is considered, and the cone in the product space is produced by the cones in its factor spaces. A completely continuous operator is in the product space defined on the bounded closed set which is the intersection of the cone with two closed balls, and the range is in the cone. Under the mixed cone expansion and compression conditions that are expressed through a class of nonnegative, positively homogeneous, concave functionals on the cone, some fixed point theorems about the completely continuous operator are proved by constructing methods and converting them into the problems of Schauder type. It is illustrated by example that the concave functionals needed here are easily constructed in a common space and on a cone in it.

Key words: fixed point completely continuous operator cone expansion and compression concave functional product space

设E是实赋范线性空间,θ表示E中的零元素,K是E中的锥,见文献^[1]. 在乘积空间E×E={(u₁,u₂)|u₁,u₂∈E}中定义范数为‖(u₁,u₂)‖=‖u₁‖+‖u₂‖. 设K₁和K₂是E中的两个锥,易证K₁×K₂为乘积空间E×E中的锥. 如果0<r_i<r_i(i=1,2),定义K_r,R=(K₁)_r₁,R₁×(K₂)_r₂,R₂,其中

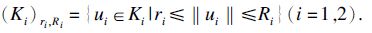
如果算子A_i:K₁×K₂→E(i=1,2)是全连续的,则称A=(A₁,A₂)是全连续的. 文献^[2]在乘积空间中证明了由锥导出的半序型锥拉伸与压缩不动点定理. 泛函型锥拉伸与压缩全连续算子的不动点定理及其应用见文献^{[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]}. 本文在乘积空间证明了几个凹泛函型混合锥拉伸与压缩条件下的不动点定理. 设α:K→[0,+∞)为凹泛函,如果α(λx)=λα(x),∀λ≥0,∀x∈K,则称α正齐次.

1 主要结论

以下均假设A=(A₁,A₂):K_r,R→K₁× K₂全连续,α_i:K_i→［0,+∞)是非负正齐次凹泛函,α_i(x)>0,∀x∈K_i\{θ} (i=1,2).

定理1 如果下列条件满足:

‖u₁‖=r₁⇒α₁(A₁(u))≥α₁(u₁),

‖u₁‖=R₁⇒α₁(A₁(u))≤α₁(u₁),

‖u₂‖=r₂⇒α₂(A₂(u))≥α₂(u₂),

‖u₂‖=R₂⇒α₂(A₂(u))≤α₂(u₂),
其中u=(u₁,u₂)∈K_r,R,那么A在K_r,R中存在不动点.

证明令h=(h₁,h₂)∈K₁×K₂,h_i≠θ (i=1,2). 定义A :K₁×K₂→K₁×K₂如下(其中记［r_i]= r_i/‖u_i‖,[R_i]=R_i/‖u_i‖ (i=1,2)):

如果u₁=0或u₂=0,则A (u)=h;

如果0<‖u₁‖<r₁且0<‖u₂‖<r₂,则A(u)=min{[r₁]^－1,[r₂]^－1}A([r₁]u₁,[r₂]u₂)+ (1－min{[r₁]^－1,[r₂]^－1})h;

如果0<‖u₁‖<r₁且r₂≤‖u₂‖≤R₂,则

A(u)=[r₁]^－1A([r₁]u₁,u₂)+(1－[r₁]^－1)h;

如果0<‖u₁‖<r₁且‖u₂‖>R₂,则

A(u)=[r₁]^－1A([r₁]u₁,[R₂]u₂)+(1－[r₁]^－1)h;

如果r₁≤‖u₁‖≤R₁且0<‖u₂‖<r₂,则

A(u)=[r₂]^－1A(u₁,[r₂]u₂)+(1－[r₂]^－1)h;

如果r₁≤‖u₁‖≤R₁且r₂≤‖u₂‖≤R₂,则 A(u)=A(u);

如果r₁≤‖u₁‖≤R₁且‖u₂‖>R₂,则

A(u)=A(u₁,[R₂]u₂);

如果‖u₁‖>R₁且0<‖u₂‖<r₂,则

A(u)=[r₂]^－1A([R₁]u₁,[r₂]u₂)+(1－[r₂]^－1)h;

如果‖u₁‖>R₁且r₂≤‖u₂‖≤R₂,则

A(u)=A([R₁]u₁,u₂);

如果‖u₁‖>R₁且‖u₂‖>R₂,则

A(u)=A([R₁]u₁,[R₂]u₂).

易见A是连续的,由于它的值域包含于紧集co {A(K_r,R)∪{h}},所以又是紧的. 根据Schauder不动点定理^[1],存在u∈K₁×K₂使得A(u)=u. 下面证明u∈K_r,R,否则与条件矛盾,于是A(u)=u. 由于h_i≠0<(i=1,2),显然‖u₁‖>0<且‖u₂‖>0.

如果0<‖u₁‖<r₁且0<‖u₂‖<r₂,不妨设min{[r₁]^－1,[r₂]^－1}=[r₁]^－1,那么

u=A(u)=[r₁]^－1A([r₁]u₁,[r₂]u₂)+(1－[r₁]^－1)h,

u₁=[r₁]^－1A₁([r₁]u₁,[r₂]u₂)+(1－[r₁]^－1)h₁.

由α₁的凹性知

α₁(u₁)≥[r₁]^－1α₁(A₁([r₁]u₁,[r₂]u₂))+(1－[r₁]^－1)α₁(h₁)>[r₁]^－1α₁(A₁([r₁]u₁,[r₂]u₂)),

α₁([r₁]u₁)=[r₁]α₁(u₁)>α₁(A₁([r₁]u₁,[r₂]u₂)).

如果0<‖u₁‖<r₁且r₂≤‖u₂‖≤R₂,则

u=A(u)=[r₁]^－1A([r₁]u₁,u₂)+(1－[r₁]^－1)h,

u₁=[r₁]^－1A₁([r₁]u₁,u₂)+(1－[r₁]^－1)h₁.

由α₁的凹性知

α₁(u₁)≥[r₁]^－1α₁(A₁([r₁]u₁,u₂))+(1－[r₁]^－1)α₁(h₁)>[r₁]^－1α₁(A₁([r₁]u₁,u₂)),

α₁([r₁]u₁)=[r₁]α₁(u₁)>α₁(A₁([r₁]u₁,u₂)).

如果0<‖u₁‖<r₁且‖u₂‖>R₂,那么

u=A(u)=[r₁]^－1A([r₁]u₁,[R₂]u₂)+(1－[r₁]^－1)h,

u₁=[r₁]^－1A₁([r₁]u₁,[R₂]u₂)+(1－[r₁]^－1)h₁.

由α₁的凹性知

α₁(u₁)≥[r₁]^－1α₁(A₁([r₁]u₁,[R₂]u₂))+(1－[r₁]^－1)α₁(h₁)>[r₁]^－1α₁(A₁([r₁]u₁,[R₂]u₂)),

α₁([r₁]u₁)=[r₁]α₁(u₁)>α₁(A₁([r₁]u₁,[R₂]u₂)).

如果r₁≤‖u₁‖≤R₁且0<‖u₂‖<r₂,则

u=A(u)=[r₂]^－1A(u₁,[r₂]u₂)+(1－[r₂]^－1)h,

u₂=[r₂]^－1A₂(u₁,[r₂]u₂)+(1－[r₂]^－1)h₂.

由α₂的凹性知

α₂(u₂)≥[r₂]^－1α₂(A₂(u₁,[r₂]u₂))+(1－[r₂]^－1)α₂(h₂)>[r₂]^－1α₂(A₂(u₁,[r₂]u₂)),

α₂([r₂]u₂)=[r₂]α₂(u₂)>α₂(A₂(u₁,[r₂]u₂)).

如果r₁≤‖u₁‖≤R₁且‖u₂‖>R₂,那么

u=A(u)=A(u₁,[R₂]u₂),从而

u₂=A₂(u₁,[R₂]u₂). 于是

α₂(A₂(u₁,[R₂]u₂))=α₂(u₂)>[R₂]α₂(u₂)=α₂([R₂]u₂).

如果‖u₁‖>R₁且0<‖u₂‖<r₂,那么

u=A(u)=[r₂]^－1A([R₁]u₁,[r₂]u₂)+(1－[r₂]^－1)h,

u₂=[r₂]^－1A₂([R₁]u₁,[r₂]u₂)+(1－[r₂]^－1)h₂,

由α₂的凹性知

α₂(u₂)≥[r₂]^－1α₂(A₂([R₁]u₁,[r₂]u₂))+(1－[r₂]^－1)α₂(h₂)> [r₂]^－1α₂(A₂([R₁]u₁,[r₂]u₂)),

α₂([r₂]u₂)=[r₂]α₂(u₂)>α₂(A₁([R₁]u₁,[r₂]u₂)).

如果‖u₁‖>R₁且r₂≤‖u₂‖≤R₂,那么

u=A(u)=A([R₁]u₁,u₂),

从而u₁=A₁([R₁]u₁,u₂). 于是

α₁(A₁([R₁]u₁,u₂))=α₁(u₁)>[R₁]α₁(u₁)=α₁([R₁]u₁).

如果‖u₁‖>R₁且‖u₁‖>R₁,那么

u=A(u)=A([R₁]u₁,[R₂]u₂),

从而u_i=A_i([R₁]u₁,[R₂]u₂). 于是

α_i(A_i([R₁]u₁,[R₂]u₂))=α_i(u_i)>[R_i]α_i(u_i)=α_i([R_i]u_i)(i=1,2).

定理2 如果下列条件满足:

‖u₁‖=r₁⇒α₁(A₁(u))≥α₁(u₁),

‖u₁‖=R₁⇒α₁(A₁(u))≤α₁(u₁),

‖u₂‖=r₂⇒α₂(A₂(u))≤α₂(u₂),

‖u₂‖=R₂⇒α₂(A₂(u))≥α₂(u₂),
其中u=(u₁,u₂)∈K_r,R,那么A在K_r,R中存在不动点.

证明因为∀u₂∈(K₂)_r₂,R₂,

([R₂]+[r₂]－1)u₂∈(K₂)_r₂,R₂,

所以可设A₁^*:K_r,R→K₁×K₂为

A₁^*(u)=A₁(u₁,([R₂]+[r₂]－1)u₂);

可设A₂^*:K_r,R→K₁×K₂为

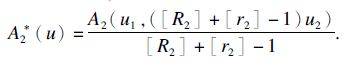
显然当‖u₂‖=r₂时,‖([R₂]+[r₂]－1)× u₂‖=R₂;当‖u₂‖=R₂时,‖([R₂]+[r₂]－1)u₂‖=r₂. 因此算子A^*=(A₁^*,A₂^*)满足定理1的条件,从而A^*存在不动点v=(v₁,v₂)∈K_r,R.

令u=(u₁,u₂)为u₁=v₁,

u₂=(R₂/‖v₂‖+r₂/‖v₂‖－1)v₂,

易见u=(u₁,u₂)∈K_r,R是A的不动点.

定理3 如果下列条件满足:

‖u₁‖=r₁⇒α₁(A₁(u))≤α₁(u₁),

‖u₁‖=R₁⇒α₁(A₁(u))≥α₁(u₁),

‖u₂‖=r₂⇒α₂(A₂(u))≥α₂(u₂),

‖u₂‖=R₂⇒α₂(A₂(u))≤α₂(u₂),

其中u=(u₁,u₂)∈K_r,R,那么A在K_r,R中存在不动点.

证明因为∀u₁∈(K₁)_r₁,R₁,

([R₁]+[r₁]－1)u₁∈(K₁)_r₁,R₁,

所以可设A₁^**:K_r,R→K₁×K₂为

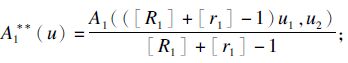
可设A₂^**:K_r,R→K₁×K₂为

A₂^**(u)=A₂(([R₁]+[r₁]－1)u₁,u₂).

显然当 ‖u₁‖=r₁时,‖([R₁]+[r₁]－1)× u₁‖=R₁; 当‖u₁‖=R₁时,‖([R₁]+[r₁]－1)u₁‖=r₁. 因此算子A^{* *}=(A₁^**,A₂^**)满足定理1的条件,从而A^{* *}存在不动点v=(v₁,v₂)∈K_r,R.

令u=(u₁,u₂)为u₂=v₂,

u₁=(R₁/‖v₁‖+r₁/‖v₁‖－1)v₁,

易见u=(u₁,u₂)∈K_r,R是A的不动点.

定理4 如果下列条件满足:

‖u₁‖=r₁⇒α₁(A₁(u))≤α₁(u₁),

‖u₁‖=R₁⇒α₁(A₁(u))≥α₁(u₁),

‖u₂‖=r₂⇒α₂(A₂(u))≤α₂(u₂),

‖u₂‖=R₂⇒α₂(A₂(u))≥α₂(u₂),

其中u=(u₁,u₂)∈K_r,R,那么A在K_r,R中存在不动点.

证明因为∀u₁∈(K₁)_r₁,R₁,

([R₁]+[r₁]－1)u₁∈(K₁)_r₁,R₁,

∀u₂∈(K₂)_r₂,R₂,

([R₂]+[r₂]－1)u₂∈(K₂)_r₂,R₂,

所以可设A₁^{* * *}:K_r,R→K₁×K₂为

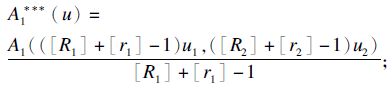
可设A₂^{* * *}:K_r,R→K₁×K₂为

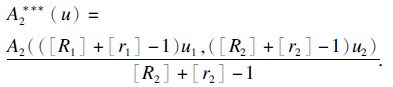
因此算子A^{* * *}=(A₁^{* * *},A₂^{* * *})满足定理1的条件,从而A^{* * *}存在不动点v=(v₁,v₂)∈K_r,R.

令u=(u₁,u₂)为

u₁=(R₁/‖v₁‖+r₁/‖v₁‖－1)v₁,

u₂=(R₂/‖v₂‖+r₂/‖v₂‖－1)v₂,

易见u=(u₁,u₂)∈K_r,R是A的不动点.

2 结语

设E=C(G)为N维欧氏空间R^N中非空有界闭集G上的连续函数空间,令

其中ε>0,G₀<是G的非空闭子集. 显然K是E中的锥,定义

于是α是锥K上的非负正齐次凹泛函,并且α(x)>0,∀x∈K＼{θ}.

参考文献

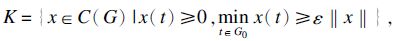
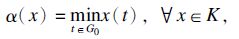
[1]	郭大钧.非线性泛函分析[M].2版.济南:山东科学技术出版社,2001. (Guo Da-jun.Nonlinear functional analysis [M].2nd ed.Jinan:Shandong Science and Technology Press,2001.)(2)
[2]	Precup R. A vector version of Krasnoselskii fixed point theorem in cones and positive periodic solutions of nonlinear systems[J].Journal of Fixed Point Theory and Applications, 2007,2(1):141-151. (1)
[3]	Avery R,Henderson J,O’Regan D.Four functionals fixed point theorem[J].Mathematical and Computer Modelling,2008,48(7/8):1081-1089.(1)
[4]	Anderson D R,Zhai C.Positive solutions to semi-positone second-order three-point problems on time scales[J].Applied Mathematics and Computation,2010,215(10):3713-3720.(1)
[5]	Cabada A, Cid J A.Existence of a non-zero fixed point for nondecreasing operators via Krasnoselskii’s fixed point theorem[J].Nonlinear Analysis:Theory,Method & Applications,2009,71(5/6):2114-2118.(1)
[6]	费祥历,王峰,陈云.关于一个新泛函的锥拉伸与压缩不动点定理及应用[J].纯粹数学与应用数学,2010,26(4):547-553. (Fei Xiang-li,Wang Feng,Chen Yun.A cone expansion and compression fixed point theorem about a new functional and its applications[J].Pure and Applied Mathematics,2010,26(4): 547-553.)(1)
[7]	Han W,Jin Z,Kang S.Existence of positive solutions of nonlinear m-point BVP for an increasing homeomorphism and positive homomorphism on time scales[J].Journal of Computational and Applied Mathematics,2009,233(2):188-196.(1)
[8]	Sun D D, Zhang G W.Computing the topological degree via semi-concave functionals[J].Topological Methods in Nonlinear Analysis,2012,39(1):107-117.(1)
[9]	Wong J S W.Existence of positive solutions for second order multi-point boundary value problems[J].Differential Equations & Applications,2012,4(2):197-219.(1)
[10]	Wang F,Zhang F,Yu Y.Existence of positive solutions of Neumann boundary value problem via a convex functional compression-expansion fixed point theorem[J].Fixed Point Theory,2010,11(2):395-400.(1)
[11]	Zhai C. Positive solutions for semi-positone three-point boundary value problems[J].Journal of Computational and Applied Mathematics,2009,228(1):279-286.(1)
[12]	Zhang H, Sun J.Existence of positive solution to singular systems of second-order four-point BVPs[J].Journal of Applied Mathematics and Computation,2009,29(1/2):325-339.(1)
[13]	Zhang G W, Sun J X.A generalization of the cone expansion and compression fixed point theorem and applications[J].Nonlinear Analysis:Theory,Method & Applications,2007,67(2):579-586.(1)

本文献在全文中的定位：

... 范线性空间,θ表示E中的零元素,K是E中的锥,见文献^[1]. 在乘积空间E×E={(u₁,u₂)|u₁ ...[View in article]

... K_r,R)∪{h}},所以又是紧的. 根据Schauder不动点定理^[1],存在u∈K₁×K₂使得 ...[View in article]

本文献在全文中的定位：

... 全连续的,则称A=(A₁,A₂)是全连续的. 文献^[2]在乘积空间中证明了由锥导出的半序型锥拉伸与压缩不动点定理. 泛函 ...[View in article]

本文献在全文中的定位：

... 点定理. 泛函型锥拉伸与压缩全连续算子的不动点定理及其应用见文献^{[3, 4, 5,
...[View in article]}

本文献在全文中的定位：

... 算子的不动点定理及其应用见文献^{[3, 4, 5, 6,
...[View in article]}

本文献在全文中的定位：

... 算子的不动点定理及其应用见文献^{[3, 4, 5, 6,
...[View in article]}

本文献在全文中的定位：

... 算子的不动点定理及其应用见文献^{[3, 4, 5, 6,
...[View in article]}

本文献在全文中的定位：