Corresponding author: LIU Qian, E-mail: liuqian0902@yeah.net
切换系统作为一类混杂动态系统,在飞行器控制、 机器人控制等领域均有着广泛的应用前景,对于切换系统的研究已取得了一定成果[1, 2, 3, 4, 5].最近,针对切换系统在状态受限条件下的控制问题引起了广泛关注[6, 7, 8, 9, 10]. 现有结果只解决了切换系统的一类跟踪问题,而H∞控制问题作为一类重要的鲁棒控制问题尚未涉及; 同时前人在控制器设计过程中只假设虚拟控制器存在,并未给出其具体形式,而设计出每步虚拟控制器的具体形式对给出系统最终的状态反馈控制器十分重要.
本文研究了一类在任意切换条件下带有状态约束的非线性切换系统的全局H∞控制器设计问题,采用障碍Lyapunov函数方法处理状态受限问题,利用反步设计技术构造出每步的共同虚拟控制器,从而得到具体的状态反馈控制器的设计方案; 最后通过数值仿真算例说明了所得结果的有效性.
1 系统描述与准备工作考虑以下非线性切换系统:
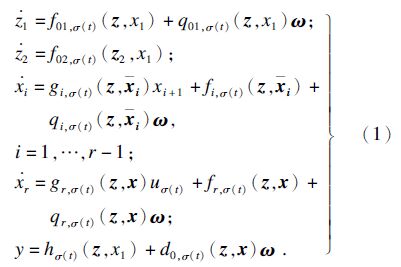
其中: z,x,ω分别为状态及扰动输入;z=(z1,z2) T,(z1,z2)∈ R n1+n2,n=n1+n2+r; x= (x1,x2,…,xr)T,xi=(x1,x2,…,xi)T; σ(t)∈M={1,…,m}为切换信号; uσ(t)为各子系统的控制输入;假设gi,σ(t)( z,xi)>0,存在常数γd0>0,有‖d0,k (z,x) ‖≤γd0. 另gi,k(0,0)=0,fi,k(0,0)= 0,hk(0,0)=0,d0,k(0,0)=0,∀k∈M. 系统(1)的前两个方程为零动态方程.
本文研究在任意切换下的系统的H∞控制问题,给定标量γ>γd0≥0,设计控制器u使得:
1) 当 ω =0时,闭环切换非线性系统在任意切换下为全局渐近稳定的;
2) 对于任意初始条件( z 0,x0)∈ R n及所有 ω ∈L2 ,存在W: R n→ R +有W (0,0)=0,使得
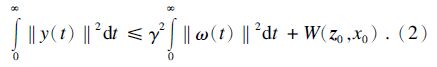
下面给出系统(1)在状态受限条件下H∞状态反馈控制器的设计过程.
引理1[8] 对任意正整数c,d及函数γ(x,y)>0, 
 .
.
定理1 假设存在光滑正定的径向无界函数W1( z 1),W2( z2) ,有

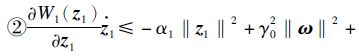 υ1( z 2,x1);
υ1( z 2,x1);
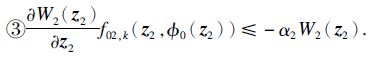
证明 第一步: 考虑系统(1)的( z1,z2,x1)方程,取η1=x1-φ0( z2) ,其中φ0( z2) 取自③, 其中,
其中, .
.
由文献[8],可知存在 满足不等式
满足不等式
由引理1[8]可得
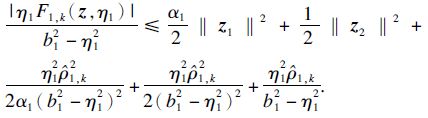
在此,本文定义
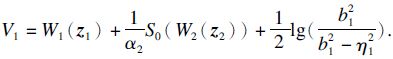
设 ,…,r-1,由条件①,②,③得到
,…,r-1,由条件①,②,③得到
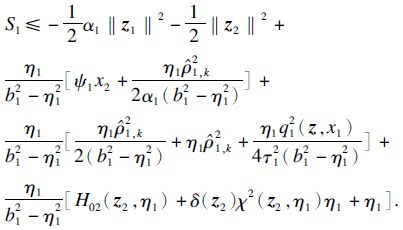
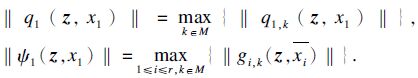
取虚拟控制器为
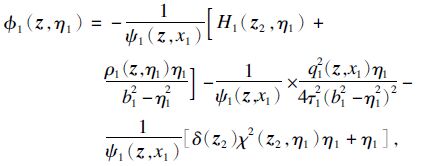
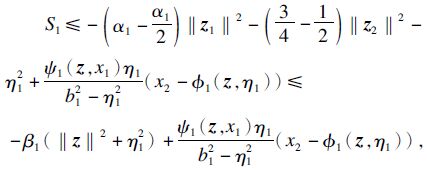
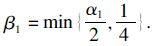
第i步(i=2,…,r-1): 利用递推法,假设第i-1步中存在i-1个正数ε1,ε2,…,εi-1,满足γd0<ε1<ε2<…<γ,φ0( z 2),φj( z ,η1,…,ηj),φ0(0)=0,φj(0)=0,j=1,…,i-1,则存在全局的坐标变换:
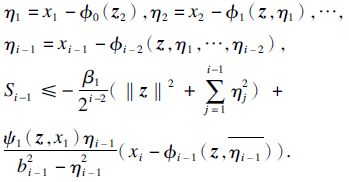
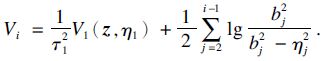
类似第一步,同理可得存在光滑的虚拟控制φi-1( z ,η1,…,ηi-1)使得

第r步: 得到控制器
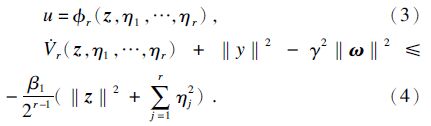
当 ω ≡0时,由式(4),有 , ∀( z ,η1,…,rη)≠0,∀k∈M,得到渐近稳定性.
, ∀( z ,η1,…,rη)≠0,∀k∈M,得到渐近稳定性.
在任意初始状态下,将式(4)两端从t=0到t=∞积分,有
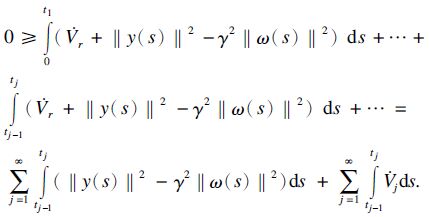
因此,本文中所定义的切换系统在控制器(3)作用下满足H∞控制问题的需要.
3 数值算例考虑由如下切换子系统构造的切换系统:
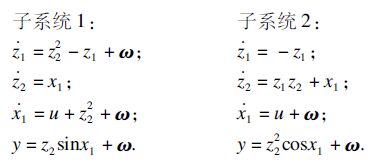
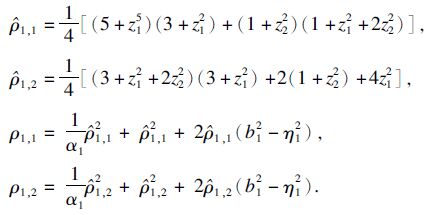
ρ1,δ(z2),χ2(z2,η1),τ21按照定理1的计算公式给出,|x1|<b1,其他参数选取及计算公式与文献[7]中相同. 有
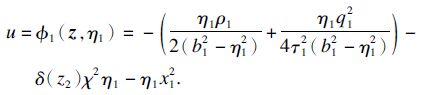
由定理1即可得到切换系统的全局H∞控制器. 图 1及图 2为在扰动ω设为e-0.1t时对应的切换系统的仿真结果.

|
图1 状态轨迹 Fig. 1 State trajectories |

|
图2 切换信号 Fig. 2 Switching signal |
本文针对状态受限下的非线性切换系统设计了H∞状态反馈控制器,并给出构造每步的虚拟控制器的具体方法,最后通过数值仿真说明了所得结果的有效性.
| [1] | Liberzon D.Switching in systems and control[M].Boston:Birkhauser,2003:17-51.( 1) 1) |
| [2] | Khalil H K.Nonlinear systems[M].Upper Saddle River:Prentice Hall,2002:588-603.( 1) 1) |
| [3] | Liberzon D,Morse A S.Basic problems in stability and design of switched systems[J]. Control Systems Magazine,1999,19(5):59-70.( 1) 1) |
| [4] | Sun X M,Lin G P,Zhao J.Stability analysis for networked control systems based on average dwell time method[J].International Journal of Robust and Nonlinear Control,2010,20(15):1774-1784.( 1) 1) |
| [5] | Ma R C,Zhao J,Dimirovski G M.H∞ controller design for switched systems in lower triangular form under arbitrary switchings[C]//The 49th IEEE Conference on Decision and Control. Atlanta:Piscataway,2010:4341-4346.( 1) 1) |
| [6] | Niu B,Zhao J.Output tracking control for a class of switched nonlinear systems with partial state constraints[J].IET Control Theory and Applications,2013,7(4):623-631.( 1) 1) |
| [7] | Su Q Y,Wang M S,Zhao J.Tracking of output-constrained switched nonlinear systems in strict-feedback form[C]// Proceedings of the 31st Chinese Control Conference. Hefei:Piscataway,2012:367-372.( 2) 2) |
| [8] | Ma R C,Dimirovski G M,Zhao J.Backstepping robust H∞ control for a class of uncertain switched nonlinear systems under arbitrary switchings[J].Asian Journal of Control, 2013,15(1):41-50.( 4) 4) |
| [9] | Tee K P,Ge S S,Tay E H.Barrier Lyapunov functions for the control of output-constrained nonlinear systems[J].Automatica, 2009,45(4):918-927.( 1) 1) |
| [10] | Ngo K B,Mahony R,Jiang Z P.Integrator backstepping using barrier functions for systems with multiple state constraints[C]// The 44th IEEE Conference on Decision and Control.Seville:Piscataway,2005:8306-8312.( 1) 1) |




