多轴段转子-支承系统是航空发动机、汽轮机和水轮机等大型旋转机械的重要组成部分，其动力学特性决定着旋转机械的工作性能和结构安全.由于转子系统受转速、离心力、离心弯矩、恢复扭矩载荷、支承刚度、陀螺力矩和尺寸效应等众多复杂因素影响，其动力学问题仅靠理论上的解析和数值模拟不能准确地解决，必须结合物理试验研究^{[1, 2, 3]}.然而，若直接对原型系统进行完全几何相似缩尺设计，不仅会加大模型试验台设计及加工的难度，增加试验成本，甚至会由于个别轴段过细或转盘过薄，给模型试验测试引入不确定因素(如转盘过薄引起颤振).此外，对于有些复杂转子系统固有特性的试验研究，只需通过简单的试验模型能够模拟再现或预测出原型的固有特性即可，但实现这一目标的前提是试验模型与原型系统必须动力学相似.因此，对复杂转子系统进行畸变试验模型的动力学相似设计方法研究非常重要.

针对转子系统的动力学相似问题研究的文献相对较少.胡培民^[4]对转子系统的相似模型建立进行了分析，分别对转子的弯曲和扭转振动响应作了研究，并且分析了刚性支承在转子弯曲振动中的相似规律.Wu^[5]研究了在低转速情况下，利用完全相似的转子系统试验模型预测原型系统横向振动特性的方法，并基于有限元法，对单盘和多盘转子系统进行了数值模拟和确认，准确预测出了转子系统的固有频率和转子径向位移响应，为该类问题的研究奠定了一定的理论基础.但在工程实际中，建立完全相似的模型试验系统非常困难，几乎是不可能的.Mohiuddin等^[6]将平衡模型降阶技术应用到复杂转子-轴承系统中，对转子系统转轴、盘和轴承单元分别建立了有限元模型，并将平衡模型降阶方程带入模型有限元方程中得到简化后的转子-轴承模型，该方法适用于阻尼很小的转子轴承系统.Young^[7]针对自适应复合材料船用发动机转子建立了动力学相似性关系，重点研究了对于影响转子和水流之间相互作用的结构参数及流体参数相似关系的建立方法，建立了转子叶片的实体模型和相似模型.

综合国内外学者研究现状，本文基于Riccati传递矩阵法和参数灵敏度分析，提出一种多轴段转子-支承系统畸变试验模型动力学相似设计方法，并通过具体算例验证所提方法的可行性.

转子-支承系统主要由转轴、转盘及支承三部分组成，多轴段模型结构示意图如图 1所示，图中Ι，Π处为省略的轴盘结构.建立坐标系oxyz，其中，坐标原点o为转子-支承系统转轴左端面中心点，x轴为转轴中心轴线，z轴为水平方向，y轴垂直于oxz平面且竖直向上为正方向.设l_j为第j个轴段长度；d_j为第j个轴段内径；D_j为第j个轴段外径；_j为第j个圆盘外径，其内径为D_j；h_j为第j个圆盘厚度；设转轴及转盘材料弹性模量为E，密度为ρ；第k个支承的支承刚度为k_k.

图 1(Figure 1)

Fig. 1

图1 多轴段转子-支承系统模型 Fig. 1 Multiaxial rotor-bearing system model

动力学相似试验模型的设计可通过以下步骤进行：①首先依据设计条件和灵敏度分析进行试验模型的简化设计，即动力学模化；②在此基础上进行必要的模型修正；③对修正后的畸变模型根据动力学相似关系进行缩尺设计得到最终试验模型.

转子-支承系统的临界转速与各参数有关，即转子-支承系统各参数的微小变化都将不同程度引起某一阶临界转速的变化.因此动力学模化前后系统各参数的微小变化必将不同程度引起前任意阶固有特性的变化.为简化说明，本文多轴段转子-支承系统动力学模化的基本思想：保证动力学模化前后前两阶临界转速一致(同样适用于使试验模型的临界转速增大或降低的设计方法).因轴段的转动惯量与圆盘相比可忽略不计，故可将轴段集总为两端相同质量点及弹性无质量轴，圆盘简化为无厚度薄圆盘.

设所设计畸变模型各段转轴的内外径均相等，转轴的内外径分别为d′和D′，转盘的内径与转轴的外径相等，即等于D′，则动力学模化前后系统第j个节点质量的变化Δm_j及第j个轴段抗弯刚度的变化Δ(EI)_j必将引起前两阶临界转速的变化，其临界转速的变化值ΔN_i(i=1,2)为

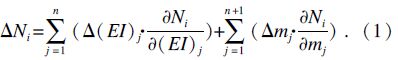
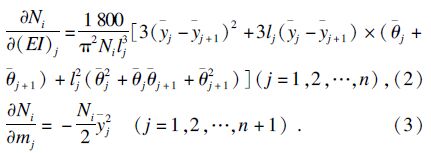
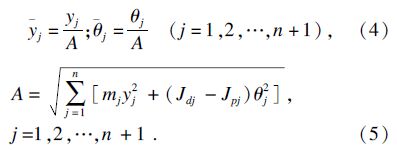
构建系统前两阶临界转速相对误差的平方和函数:

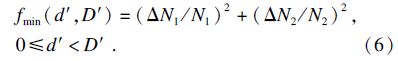
根据式(6)，基于Matlab数学求解函数库中的最优化求解方法，求出最优解d′，D′.

由于式(2)、式(3)均是在对原系统方程求导，且在略去了二阶以上微量条件下得出的，因此只有在参数变化微小情况下才是准确的，故必须对上述求得的畸变模型的d′,D′进行修正.

设修正后畸变模型的两个参数为d″，D″，假设系统前两阶临界转速的改变量为{Δ N}=[Δ N₁ ′,Δ N₂ ′]^T，需调整参数的修改量为 {Δp}=[Δm₁′,Δm₂ ′,…,Δm_n+1 ′,ΔEI₁′,ΔEI₂′,…,ΔEI_n′]^T，则有

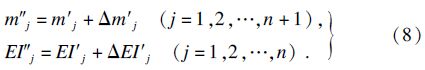
根据式(7)和式(8)，基于Matlab多项式型方程的准解析解法，求出d″和D″.然后根据结点质量及转动惯量不变的原则，计算出修正后的畸变模型转盘的外径及厚度.最后根据Riccati传递矩阵法计算修正后的畸变模型的临界转速和固有特性，判断是否能保证前两阶临界转速相对误差小于等于给定范围(如5 % ).若不满足，按上述方法继续修正，直到满足要求为止.

对于多轴段转子-支承系统，经上述动力学模化及模型修正后，欲研究原型转子-支承系统动力学特性，则缩尺模型的建立尤为必要，缩尺设计的基本理论依据为^[9]

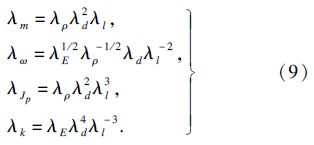
设某空压机高压转子如图 2所示^[10]，转子模 型的数据如表 1、表 2所示.转子材料的弹性模量E=206.0GPa，密度为7850kg/m³，支承在结点9和17处，支承刚度均为22MN/m.根据本文提出的多轴段转子-支承系统畸变模型动力学相似设计方法，首先对原型系统进行动力学模化得到畸变模型.然后修正，最后根据式(9)，令λ_ω=λ_E^1/2λ_ρ^－1/2λ_dλ_l^－2=1，采取相似比：λ_d=1/2，λ_l= 2 /2，λ_k= 2 /8，设计缩尺模型，则其缩尺模型尺寸参数如表 3所示，在结点9和17处缩尺模型支承刚度均为3.9×10⁶N/m.因结点1和25处附加转动惯量及附加质量很小，故忽略，因此结点1和25无转盘.采用Riccati传递矩阵法分别计算原型及缩尺模型的临界转速，其临界转速对比值如表 4所示，振型图如表 5所示.

图 2(Figure 2)

Fig. 2

图2 某空压机高压转子的模型 Fig. 2 Air compressor high-pressure rotor model 1—Ι级叶轮; 2—П级叶轮; 3—小齿轮; 4—密封套; 5—甩油盘; 6—推力盘.

表1

Table 1

表1(Table 1)

表1 高压转子模型数据表 Table 1 Data sheet of high-pressure rotor model 结点 轴段长度/m 刚度外径/m 质量外径/m 1 0.023 0.024 0.026 2 0.029 0.050 0.050 3 0.037 0.050 0.050 4 0.038 0.050 0.063 5 0.039 0.050 0.063 6 0.038 0.050 0.063 7 0.045 0.055 0.074 8 0.046 0.060 0.060 9 0.031 0.060 0.060 10 0.040 0.075 0.154 11 0.006 0.090 0.090 12 0.053 0.100 0.107 13 0.053 0.100 0.107 14 0.006 0.090 0.090 15 0.040 0.075 0.154 16 0.031 0.060 0.060 17 0.046 0.060 0.060 18 0.045 0.055 0.074 19 0.038 0.050 0.063 20 0.039 0.050 0.063 21 0.038 0.050 0.063 22 0.035 0.050 0.050 23 0.032 0.050 0.050 24 0.023 0.024 0.026 25 0.000 - -

表1 高压转子模型数据表 Table 1 Data sheet of high-pressure rotor model

表2

Table 2

表2(Table 2)

表2 高压转子模型数据表 Table 2 Data sheet of high-pressure rotor model 结点 附加直径转动惯量/(kg · m2) 附加极转动惯量/(kg · m2) 附加质量/kg 1 0.0003 0.0004 0.804 3 0.0790 0.1344 15.793 23 0.0694 0.1185 15.396 25 0.0003 0.0004 0.776

表2 高压转子模型数据表 Table 2 Data sheet of high-pressure rotor model

表3

Table 3

表3(Table 3)

表3 缩尺模型参数 Table 3 Scaled model dimension parameters mm 参数 值 转轴内径 10.0 转轴外径 31.0 转轴长度 602.0 转盘1内径 31.0 转盘1外径 178.0 转盘1厚度 15.0 转盘2内径 31.0 转盘2外径 169.0 转盘2厚度 17.0

表3 缩尺模型参数 Table 3 Scaled model dimension parameters

表4

Table 4

表4(Table 4)

表4 原型及缩尺模型临界转速对比 Table 4 Comparison of critical speeds for prototype and scaled model 转速/(r · min-1) 一反 一正 二反 二正 原型 3058 3282 5622 6029 缩尺模型 3158 3342 5656 6009 相对误差/ % 3.27 1.83 0.60 0.33

表4 原型及缩尺模型临界转速对比 Table 4 Comparison of critical speeds for prototype and scaled model

表5

Table 5

表5(Table 5)

表5 前两阶振型对比 Table 5 Comparison of first two order vibration model 阶数 原型 缩尺模型 一阶 二阶

表5 前两阶振型对比 Table 5 Comparison of first two order vibration model

由表 4及表 5可以看出，转子-支承系统缩尺模型已很好再现原型前两阶固有特性.

1) 基于Riccati传递矩阵法和灵敏度分析提出了一种多轴段转子-支承系统畸变试验模型的动力学相似设计方法.

2) 以设计某空压机高压转子的缩尺试验模型为例，给出具体缩尺试验模型的设计步骤和方法，进一步确认了设计方法的有效性和实用性.

3) 为简化说明，本文以保证动力学模化前后前两阶的临界转速一致为例加以说明，实际上该方法对于保证更多阶次临界转速和更多固有特性(包括振型) 参数一致或成比例的设计都有实际指导意义，只是畸变模型待求转轴参数亦相应增加.