Corresponding author: LI Hui, E-mail: lh200300206@qq.com
压电陶瓷具有体积小、质量轻、频响高等优点,在光学、电子、航天航空等领域得到了一定程度的应用[1, 2].研究人员也逐步将其作为高频振动激励设备使用.例如,张益松等[3]将压电陶瓷应用到平板结构的振动试验中.林立等[4]将压电陶瓷薄膜贴于圆柱壳体中间一圈作为激励,实验获得了自由状态下的单层圆柱壳以及带有不同厚度阻尼层的双层圆柱壳的频响曲线.Ivancic等[5]利用压电陶瓷对硬涂层悬臂薄板进行扫频激励,来识别该复合结构的固有频率和阻尼.黄爱萍[6]在压气机轮盘轮缘和辐板上布置了12片压电陶瓷并对其激励,采用激光全息干涉法获取轮盘7阶振动模态的静频和振型.
由于压电陶瓷在高频激振方面相对于力锤、振动台等设备具有很大的优势,很多学者希望将其用于薄壁构件的高频振动测试领域.但薄壁结构壁厚薄,质量轻,若采用直接激励方式,即将陶瓷直接粘贴于被测结构表面上,将不可避免地对该类型结构带来附加刚度和质量的影响,导致频响函数发生偏移,固有频率和阻尼比等模态参数的测试结果出现误差是难以控制的[7].采用基础激励的测试方法则不会对被测结构带来任何附加质量和刚度的影响,测试状态即为结构真实的受力状态[8].因此,在利用压电陶瓷作为激振器使用时,为了准确获得薄壁构件的振动响应,应该利用其基础激励的形式,来达到最佳的测试精度.如果在激励的过程中,还能够准确获得激振幅度大小,就可以将电陶瓷应用到薄壁构件的振动响应测试领域.为此,有必要研究针对压电陶瓷激振幅度的某种标定方法.然而,由于压电陶瓷在尺寸、粘贴方式、压电陶瓷驱动电压的加载形式及其激励频率的使用范围等方面存在很大的差异,目前关于压电陶瓷直接激振或基础激振幅度的动态标定都没有统一的标准可循,常用的传感器动态标定方法,如冲击响应法、频率响应法、激振法或阶跃响应法,都需要很多专业的设备才能开展[9],且成本较高,标定过程复杂.
本文提出了一种简便而可靠的压电陶瓷基础激励下激振幅度的标定方法,详细叙述了标定流程.利用该方法对一款PZT陶瓷的基础激振幅度进行了标定,证明了方法的有效性和实用性.
1 压电陶瓷激励系统存在的问题现有振动测试中应用的压电陶瓷激励系统通常是一个开环系统,即压电陶瓷驱动电源放大后的高电压激励信号只是用来驱动陶瓷进行振动激励,没有实现激励信号的实时采集.主要问题在于绝大多数数据采集设备的安全采集电压一般都在±1 mV~±10 V范围内,不能直接采集±110~±220 V的高电压信号.
针对传统压电陶瓷激励系统存在的问题,本文研发了一款反馈衰减器,并建立了压电陶瓷激励-反馈系统,如图 1所示,该系统有效解决了加载到压电陶瓷上的高电压激励信号的实时采集问题,为压电陶瓷激振幅度的标定工作奠定了基础.
 |
图 1 压电陶瓷激励-反馈系统 Fig. 1 The piezoelectric excitation-feedback system |
悬臂梁理论比较成熟,可以通过该结构的动力学模型来较为精确地模拟和对照实验测试结果,本文采用悬臂梁作为压电陶瓷基础激励下的被测对象,如图 2所示.这里仅考虑梁的弯振,假设梁为等截面Euler-Bernoulli梁.梁的弹性模量为E,惯性矩为I,单位长度质量为m,长度为l,梁的位移响应为φ(x,t),V为截面上的剪力,M为截面上的弯矩,c为位移速度阻尼系数,cr为变形速度阻尼系数.设基础激励的表达式为y(t)=Ysin(ωt),则可以得到梁上一点的总位移为

 |
图 2 压电陶瓷基础激励下悬臂梁的动力学模型 Fig. 2 Dynamics model of cantilever beam under base excitation of piezoelectric ceramic exciter |
参考文献[10],得到弯矩和剪力的表达式为

将式(2)和式(3)代入式(1)并简化可得

整理可得

代入V的表达式并简化,可得基础激励下悬臂梁的运动方程为

引入正则坐标,按振型叠加法来求解方程(6),则悬臂梁位移响应的表达式为

悬臂梁的模态振型可表示为

对两种阻尼系数做出如下假定,α,β为待定常数,并引入阻尼比ζi得

将式(8)~(11)代入式(6)中,并根据正则坐标下的主振型的正交条件,化简可得


由式(12)可解得ηi(t),进一步在零初始条件下可将其简化为

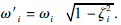 ω′i为有阻尼时第i阶固有频率.
ω′i为有阻尼时第i阶固有频率.
最终,可得到压电陶瓷基础激励下悬臂梁上任意点的响应表达式为

图 3为压电陶瓷基础激励下激振幅度的标定原理示意图,这里主要涉及3个映射:压电陶瓷基础激振幅度与理论模型基础激振幅度之间的映射;测试响应与预测响应之间的映射;理论模型的分析过程与压电陶瓷激励实验过程的映射.
 |
图 3 压电陶瓷基础激励下激振幅度的标定原理示意图 Fig. 3 Calibration principle of base excitation amplitude of piezoelectric ceramic exciter |
用建立好的压电陶瓷基础激励下悬臂梁的动力学模型来计算某激励频率和基础激振幅度下的振动响应,当梁上指定点的响应预测结果与实验测试的振动响应一致时(误差控制在3%~5%以内),便可将数值计算时输入的基础激振幅度大小(单位为g)等效成为悬臂梁在压电陶瓷实际激励电压(单位为V)作用下的激振幅度,并建立“基础激振幅度-激励电压”的对应关系,从而实现压电陶瓷基础激振幅度的标定.
3.2 标定流程及方法对压电陶瓷的基础激振幅度进行标定:
1) 组配压电陶瓷基础激励标定测试系统.首先,选择一个梁试件并通过一个通用的夹具将其一端夹紧(夹具还可用来约束其他结构件,如不同厚度的各种板和梁,且其质量相对于被测结构质量之比应大于10倍),通过游标卡尺测得该悬臂梁的尺寸参数后,将压电陶瓷激振器固定安装在夹具上(安装位置一经确定不能随意调整),其激振能量将通过夹具传递给悬臂梁;然后,利用反馈衰减器和数据采集分析仪,完成图 2所示的压电陶瓷激励-反馈系统的组配;最后,在该系统上增加激光多普勒测振仪来获取悬臂梁试件上某一测点的振动响应信号,从而实现压电陶瓷基础激励标定测试系统的组配.
2) 测试各阶固有频率及阻尼比.利用基础激励标定测试系统,进行快速正弦扫频实验,初步获得悬臂梁的各阶固有频率.确定包含每阶固有频率的扫频频段后,以一定的扫频速率再次进行扫频测试,记录测点的时域响应数据并对其进行频谱分析,通过半功率带宽法辨识出悬臂梁的各阶固有频率及阻尼比.上述结果用于修正理论模型,也为理论模型提供结构系统真实的阻尼参数.
3) 测试不同激励电压下悬臂梁的振动响应.选取要标定的激励频段,并根据激励频段大小选择若干激励频率,以这些激励频率来分别对悬臂梁试件进行正弦激励,记录悬臂梁响应测点的振动响应幅值.改变压电陶瓷的激励电压,重新激励悬臂梁并记录同一测点的振动响应.选取的激励频率和激振幅度值越多,标定就越精确.
4) 创建理论模型并通过实验数据修正.输入悬臂梁的几何及材料参数,以及测得的阻尼参数,创建压电陶瓷基础激励下悬臂梁的理论模型.计算其固有频率,并与实验测试的固有频率结果相互对照,用实验结果修正理论模型中的材料及几何参数,直到理论模型分析的结果与实验值比较接近,误差控制在5%以内.
5) 用修正后的理论模型预测梁的振动响应.在一定的基础激励幅度下,用修正后的理论模型来预测悬臂梁分析响应点对应(该点与测试响应点的位置应相同)的响应幅度.调整理论模型中基础激振的幅度,直到预测的响应幅度与实验测得的响应幅度的误差在3%以内,记录理论模型计算时输入的基础激振幅度大小,以此来对应压电陶瓷真实的基础激振幅度.
6) 完成标定.建立压电陶瓷“基础激振幅度-激励电压”的对应关系,采用最小二乘法进行曲线拟合,确定两者的数学表达式,并获得标定曲线,实现在某激励频段内压电陶瓷基础激振幅度的标定.
4 标定实例 4.1 标定系统悬臂梁试件的材料为Ti-6Al-4V,弹性模量为110.32 GPa,泊松比为0.31,密度为4 420 kg/m3,悬臂梁长、宽、厚度分别为250 mm×20 mm×1.5 mm,其被夹具夹持的长度为25 mm,PZT压电陶瓷激振器为长方体,长、宽、高为45 mm×25 mm×25 mm,将其安装在夹具的中间位置,其几何中心距悬臂梁根部位置约为5 mm,激光测振仪的激光点距离悬臂梁自由端约为3 mm.
将自行研发的反馈衰减器的两端制作成BNC的形式,利用它将加载到压电陶瓷上的高电压激励信号转变为±1 mV~±10 V的低电压信号(取决于压电陶瓷驱动电源的放大倍数),并实时地反馈给数据采集分析仪.按照3.2节论述的方法,组配如图 4所示的压电陶瓷基础激励标定测试系统,涉及的仪器包括:LMS 16通道便携式数据采集仪、Rhvd3c110 V压电陶瓷驱动电源、反馈衰减器和Polytec PDV-100激光测振仪.
 |
图 4 压电陶瓷基础激励标定测试系统 Fig. 4 Calibration and test system of base excitation amplitude of piezoelectric ceramic exciter |
利用所组配的标定测试系统获取悬臂梁的各阶固有频率、阻尼比,测试结果见表 1和表 2.并与修正后的理论模型的固有频率计算结果进行对比,由表 1可知,误差在可接受的5%范围内,故可以用理论模型来预测悬臂梁的振动响应.
| 表 1 理论模型计算与实验测试获得的悬臂梁的固有频率 Table 1 Natural frequencies of the cantilever beam obtained by methods of theoretical calculation and experimental test |
| 表 2 实验测试获得的悬臂梁的各阶阻尼比 Table 2 Damping ratios of the cantilever beam obtained by experimental test |
开展激振幅度标定实验.激励频率设定为300和450 Hz,激励电压为 0.5~3 V.利用压电陶瓷激振器分别对悬臂梁进行定频、定幅的基础激励,通过激光测振仪获得其振动速度.采用修正后的理论模型,不断调节激振幅值,直到预测的响应结果与实验测得的响应幅度达到误差允许的3%范围内.图 5,图 6分别为激励频率为300 Hz,激励电压为1 V时的激励信号与响应信号.其他激励频率与激励电压下的振动速度测试结果见表 3与表 4.根据上述结果建立“基础激振幅度-激励电压”标定曲线,如图 7所示;通过最小二乘法,并采用平均处理获得的数学表达式也列入图 7中.可见,PZT陶瓷在300~450 Hz内,其基础激振幅度与电压基本呈线性关系.
 |
图 5 300 Hz激励时1V激励电压下的激励信号 Fig. 5 Excitation signal under 300 Hz and 1V excitation voltage |
 |
图 6 300 Hz激励时1 V激励电压下的响应信号 Fig. 6 Response signal under 300 Hz and 1 V excitation voltage |
| 表 3 300 Hz激励时激振幅度标定结果及误差 Table 3 Calibration results and errors of excitation amplitude at 300 Hz |
| 表 4 450 Hz激励时激振幅度标定结果及误差 Table 4 Calibration results and errors of excitation amplitude at 450 Hz |
 |
图 7 压电陶瓷基础激振幅度的标定曲线 Fig. 7 The calibration curve of base excitation amplitude of piezoelectric ceramic |
重复上述步骤,可获得其他激励频率下压电陶瓷基础激振幅度的标定曲线,建立基础激振幅度与激励电压的对应关系.然后可以将悬臂梁试件更换为其他薄壁结构件,如用以模拟叶片特征的不同厚度的薄板.通过标定后的压电陶瓷及其安装的夹具,在明确的基础激振幅度下,采用接触或非接触测振方式获取该结构的振动响应.
例如,实际薄板的第3阶固有频率为388.3 Hz,刚好处于上述标定曲线的应用范围,此时需要测试0.5 g激励下薄板的共振响应情况,则可以对图 7所示的标定曲线进行换算,当压电陶瓷的激励电压被调整为2.29 V时,就可以满足薄板在0.5 g激励下共振响应的测试需求.
5 结 论1) 在明确标定原理的基础上,建立了压电陶瓷基础激励下的悬臂梁动力学模型,采用理论和实验相结合的方式来解决压电陶瓷基础激励下激振幅度的标定问题.
2) 对一款PZT陶瓷的基础激振幅度进行了标定.组配了压电陶瓷基础激励标定测试系统,在不同的激励频率和基础激振幅度下开展了标定实验,获得了“基础激振幅度-激励电压”标定曲线,明确了压电陶瓷激励结构时的基础激振幅度大小.
| [1] | Chu X,Ma L,Li L.A disk-pivot structure micro piezoelectric actuator using vibration mode[J]. 1) 1) |
| [2] | Damjanovic D,Newnham R.Electrostrictive and piezoelectric materials for actuator applications[J]. 1) 1) |
| [3] | 张益松,刘敏姗,伊立言.压电陶瓷片在振动试验中的应用[J].实验力学,1987,2(2):90-94.(Zhang Yi-song,Liu Min-shan,Yi Li-yan.The application of piezoelectric ceramic flakes in vibration test [J]. 1) 1) |
| [4] | 林立,何祚镛.有限长、多层复合圆柱壳减振特性的研究[J].振动工程学报,1991,4(1):52-64.(Lin li,He Zuo-yong.Study of the behavior in reduction of vibration and sound of composite shells [J]. 1) 1) |
| [5] | Ivancic F,Palazotto A.Experimental considerations for determining the damping coefficients of hard coatings[J]. 1) 1) |
| [6] | 黄爱萍.轮盘振动特性试验及共振转速特性分析[J].测控技术,2007,26(4):14-15.(Huang Ai-ping.Test of vibration character and analysis of resonance speed character for disk[J]. 1) 1) |
| [7] | Ewins D J.Modal testing:theory,practice and application[M].Baldock:Research Studies Press,2000:78-99( 1) 1) |
| [8] | Pellicano F.Dynamic instability of a circular cylindrical shell carrying a top mass under base excitation experiments and theory[J]. 1) 1) |
| [9] | Hou Y L,Yao J T,Zeng D X,et al.Development and calibration of a hyperstatic six-component force/torque sensor[J]. 1) 1) |
| [10] | Clough R W,Penzien J.Dynamics of structures[M].Berkeley:Computers & Structures Inc,1995:369-370.( 1) 1) |




