随着技术的不断发展,多旋翼飞行器成为诸多应用领域的理想解决方案,如:交通监控、搜索及救援、航空测绘等.实现多旋翼飞行器的稳定控制,需要实时获取其位置及姿态数据.它们可以通过不同的方式获取,如捷联惯性导航系统(SINS)与全球卫星定位系统(GPS).现代微机电系统(MEMS)技术可以提供适合飞行器使用的惯性测量单元(IMU)[1]与GPS模块等.
SINS具有较强的自主性和全面的信息,但定位误差随时间而积累,因此很难独自完成高精度和长航时任务.GPS可以在全球范围内、各种天气条件下,实现高精度三维定位和速度测量,并且其位置误差不随时间而积累;但是,GPS卫星不完全覆盖地球,特别是在中纬度的所谓“间隙区域”处.SINS和GPS具有互补性,并且两种系统的协同应用已被广泛研究[2,3,4,5,6,7].应用低成本的SINS/GPS组合导航,定位精度可以达到米级.
为提高组合导航系统的定位精度,常采用不同的滤波方法处理定位数据.无味滤波(UKF)具有较高的精度,但计算复杂[8];粒子滤波(PF)选择先验概率密度函数作为重要密度函数,但其没有考虑当前测量值,并且样本的重要性概率密度和真实的后验概率密度有很大不同[9,10];扩展卡尔曼滤波(EKF)是一种次优滤波,其与最新的测量值相结合,通过连续的高斯估计更新后验分布,实现递归估计.
目前获取地形边界与面积的常用方法有:采用卫星或飞机远程拍摄高分辨率图像;使用Google Earth或Google Map等软件;使用设备实地测量等.这些方法成本高,估计精度低,效率低.本文提出一种以四旋翼飞行器作为测量平台,实时且低成本的不规则地形边界与面积估计算法.使用飞行器的前视和下视摄像头确定飞行方向和选择边界点;采用SINS/GPS组合导航系统获取地形边界点的定位数据;应用Pauta准则剔除异常定位数据;使用扩展卡尔曼粒子滤波(EKPF)方法提高定位数据精度,并将估计后的定位数据作为边界点的最终位置,其结合了EKF与PF的优点.经过滤波处理后,定位精度可达亚米级.实际飞行试验结果验证了该算法的可行性和准确性,估计误差小于±1.2%.与类似方法相比[11],该算法精度提高0.8%~3.4%.
1 定位数据处理方法
为得到更精确的初始边界点定位数据,本文算法采用SINS/GPS紧耦合的组合导航方式.为确保导航系统的可靠性,GPS模块至少要同步观测到四颗卫星,飞行器在边界点悬停并获取该点的定位数据,算法分别使用Pauta准则与EKPF方法剔除异常定位数据和进一步优化、估计该点的最终位置.算法按照上述过程依次获取全部边界点的定位数据,并依据边界点的最终位置自动估计地形的边界与面积.算法执行过程中,飞行器通过机身自带的前视与下视摄像机确定飞行方向与选择边界点.图1为简化的系统结构.
 |
图 1 简化的系统结构 Fig. 1 Simplified structure of system |
Pauta准则(3σ准则)是常用的简单、有效的粗大误差判别准则.其假设待检测数据中只含有随机误差,据此计算得到标准偏差;按一定概率确定一个区间,超过这个区间的误差为粗大误差并予以剔除.通常,在飞行器悬停获取定位数据时,由于飞行器悬停稳定性及其他因素的影响,定位数据中可能会存在异常数据,因此在使用EKPF前,本算法使用Pauta准则剔除异常定位数据.假设采集到的定位数据为独立样本数据Xi (i=1,2,…,n).定义样本的算数平均值为x,残差为Ei=Xi-x,样本的标准偏差为S.如果样本中数据Xi的残差满足:


将式(2)代入贝塞尔公式得到优化后的标准偏差:

剔除异常定位数据后,使用EKPF方法进一步提高定位精度.定义EKPF的重要概率密度函数为

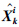 是时间k处的状态估计;
是时间k处的状态估计;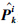 是时间k处的方差估计;Zk为时间k处的量测值.与粒子滤波相比,EKPF可以得到较好的重要性密度函数,并将先验分布向高可能性的区域移动.对于具有高斯白噪声和量测噪声的弱非线性系统,EKPF克服了现有的经典粒子滤波的问题.
是时间k处的方差估计;Zk为时间k处的量测值.与粒子滤波相比,EKPF可以得到较好的重要性密度函数,并将先验分布向高可能性的区域移动.对于具有高斯白噪声和量测噪声的弱非线性系统,EKPF克服了现有的经典粒子滤波的问题.定义EKPF的系统状态方程为

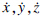 ]T.式中x,y,z为经、纬度与高度数据;
]T.式中x,y,z为经、纬度与高度数据;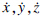 为经、纬度与高度方向的速度分量.
为经、纬度与高度方向的速度分量.定义EKPF的系统量测方程为


EKPF算法流程如下.
①初始化:对先验概率采样并生成粒子X0i(i=1,…,N).所有粒子都服从先验概率分布p(X0),即X0i ~ p(
X0).设置粒子的权重为ω0i=1/N且 =var(X0).
=var(X0).
②使用EKF更新粒子:离散的非线性EKF方程为式(8),其中T为采样周期.

③生成新粒子:Xik~q(Xik|Xik-1,
Zk)=N(
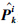 ).
).
④计算新粒子权重:

⑤归一化权重:

⑥状态估计:

在高斯平面坐标系中,算法定义所有边界点的位置数据格式为pdi= (xi,yi,yawi,marki),i=0,1,…,N.xi与yi分别为高斯平面坐标系中的位置;yawi为飞行器由边界点i到i+1的偏航角;marki为边界点i的凹、凸点标记.图2为估计算法的流程图.
 |
图 2 估计算法流程图 Fig. 2 Flow chart of estimation algorithm |
本文提出的边界与面积估计算法主要流程为:弧段起始点与结束点判断;待估计地形的凹凸点判断;局部极值点判断;最终面积估计过程中的二次凹点判断.由于边界点分为顺时针选择与逆时针选择两种,因此,在弧段判断及最终面积估计的过程中,分别引入了各自的判断规则.图3与图4分别为简化的算法演示图.
 |
图 3 简化的顺时针估计演示
Fig. 3 Simplified demo of clockwise estimation(a)—待估计地形; (b)—凹凸点判断后; (c)—预估计地形; (d)—二次预估计地形(spta). |
 |
图 4 简化的逆时针估计演示
Fig. 4 Simplified demo of counterclockwise estimation(a)—待估计地形; (b)—凹凸点判断后; (c)—预估计地形; (d)—二次预估计地形(spta). |
3.1 实验过程
本文通过实际的飞行测试,验证了EKPF方法的有效性及地形边界与面积估计算法的准确性.表1为待估计地形边界点的位置数据 (源自Google Earth).测试当天南风,风速0.8~3.6 m/s,待估计地形周围无任何障碍物;飞行器飞行高度3 m,速度2~4 m/s;飞行器在每个边界点悬停1 min,获取240个定位数据;EKPF采样周期T=250 ms;考虑算法精度、速度与方便实际应用,选择粒子数N=500,

| 表 1 边界点位置数据 Table 1 Positioning data of boundary points |
图5给出了EKPF方法滤波前后经、纬度定位数据的对比.由于不知道当前边界点的实际精确位置,因此,将定位数据的经、纬度平均值作为该点的参考位置.图中实线为滤波前的定位数据相对于参考位置的绝对误差;虚线为使用EKPF优化后的各点绝对误差.经过EKPF方法后,修正的绝对误差显著减小,定位精度达到亚米级.
 |
图 5 EKPF滤波前后定位对比 Fig. 5 Positioning before and after EKPF filtering |
算法采用航线法获取最终的地形边界估计与面积估计.图6与图7分别给出了实际飞行测试的结果.经过实地测量,待估计地形的实际面积为34 845.471 3 m2,算法经过计算后得出的结果是35 227.970 0 m2,误差为+1.097 7%.
 |
图 6 实际飞行测试结果 Fig. 6 Actual flight test result |
 |
图 7 Google Earth中的实际飞行测试结果 Fig. 7 Actual flight test result in Google Earth |
通过实际飞行测试可以验证:在使用Pauta准则剔除异常数据后,EKPF对提高定位精度非常有效;与只使用SINS/GPS组合导航系统相比,定位精度由米级提高至亚米级;地形边界与面积 估计算法的精度达到设计要求,估计误差小于±1.2%.与使用Google Earth与Google Map等方法相比,该算法精度较高,精度提高约5.5%;与王陈陈等[11]提出的类似方法相比,该算法精度提高0.8%~3.4%.综上所述,本文采用的EKPF方法、地形边界与面积估计算法是可行、准确的.
| [1] | de Marina H G,Pereda F J,Giron-Sierra J M,et al.UAV attitude estimation using unscented Kalman filter and TRIAD[J]. IEEE Transactions on Industrial Electronics,2012,59(11):4465-4474. ( 1) 1)
|
| [2] | Brown R G,Hwang P Y C.Introduction to random signals and applied Kalman filtering[M].New York:John Wiley & Sons,1992. ( 1) 1)
|
| [3] | Jwo D J,Yang C F,Chuang C H,et al.A novel design for the ultra-tightly coupled GPS/INS navigation system[J].Journal of Navigation,2012,65(4):717-747. ( 1) 1)
|
| [4] | Li Y,Efatmaneshnik M,Dempster A G.Attitude determination by integration of MEMS inertial sensors and GPS for autonomous agriculture applications[J].GPS Solutions,2012,16(1):41-52. ( 1) 1)
|
| [5] | Wang W,Liu Z,Xie R.Quadratic extended Kalman filter approach for GPS/INS integration[J].Aerospace Science and Technology,2006,10(8):709-713. ( 1) 1)
|
| [6] | 韩厚增,王坚,李增科,等.基于EKPF的GPS导航模型研究[J].大地测量与地球动力学,2013,33(2):139-142. ( 1) 1)
|
| [7] | 吴平,雷虎民,邵雷.捷联惯性导航系统加速度计误差建模与标定补偿[J].弹箭与制导学报,2010,30(5):5-8. ( 1) 1)
|
| [8] | Julier S J,Uhlmann J K,Durrant-Whyte H F.A new approach for filtering nonlinear systems[C]// Proceedings of the 1995 American Control Conference.Seattle,1995:1628-1632. ( 1) 1)
|
| [9] | Gordon N J,Salmond D J,Smith A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].Radar and Signal Processing,1993,140(2):107-113. ( 1) 1)
|
| [10] | Rigatos G G.Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles[J].Robotics and Autonomous Systems,2012,60(7):978-995. ( 1) 1)
|
| [11] | 王陈陈,马明建,马娜,等.基于GPS的土地面积测量算法[J].山东理工大学学报:自然科学版,2013,27(4):64-68. ( 2) 2)
|


