Corresponding author: ZHOU Bing-hai, E-mail: bhzhou@tongji.edu.cn
对于Job Shop调度问题,大多数研究都不考虑搬运设备,而仅仅对机床进行调度.考虑物料搬运的Job Shop调度问题更贴近实际生产.
近年来,一些学者在研究传统Job Shop调度的基础上,对考虑物料搬运的Job Shop调度问题进行了研究.文献[1]提出了考虑物料搬运的Job Shop调度问题,但未研究求解算法.文献[2, 3]针对考虑一个搬运设备的Job Shop调度问题,分别提出了基于禁忌搜索算法的两阶段算法和并行禁忌搜索算法.文献[4]针对含有一个机器人的制造单元调度问题,提出了改进遗传算法.近来,有学者对考虑多个物料搬运设备的Job Shop调度问题进行了研究.文献[5]针对带多个搬运设备的Job Shop调度问题,提出了一个局域搜索算法.文献[6]针对带多个搬运设备的Job Shop调度问题,设计了一种文化基因算法.文献[7]对带多个搬运设备的柔性Job Shop调度问题进行了研究,同时构造了局域搜索算法.文献[8]对考虑多个搬运设备的加工时间不确定的柔性Job Shop调度问题进行了研究,同时提出了遗传算法和禁忌搜索算法的混合算法.上述对考虑物料搬运的Job Shop调度问题的研究均使用元启发式算法(meta heuristic algorithms),求解比较耗时.结构式启发式算法(structured heuristic algorithms)求解速度快,然而关于此类算法的研究却较为少见.
本文在上述文献研究的基础上,以最小化最大完工时间makespan为调度目标,利用改进析取图建立调度模型,在引入析取子图的基础上,构建了两阶段构造式启发式算法.
1 问题描述与建模带物料搬运设备的Job Shop调度问题可以描述为:n个工件{J1,J2,…,Jn}在m台机床{M1,M2,…,Mm}上加工,工件Ji包括ni个工序Oi,j(j=1,2,…,ni),每个工序Oi,j对应一台机床M(Oi,j),其加工时间pi,j为定值.当工序Oi,j在机床M(Oi,j)上完成加工之后,触发搬运工序Ti,j.搬运过程如下:工件Ji在机床M(Oi,j)上等待搬运,发出搬运请求之后,搬运设备R先从当前位置空载行驶到机床M(Oi,j),加载工件,然后负载将工件Ji搬运至下一道工序Oi,j+1对应的机床M(Oi,j+1)处.考虑搬运工序之后,工件的实际工序顺序可以表示为 Oi,j < Ti,jOi,j+1 <Ti,j+1 <… <Oi,ni (Oi,j < Ti,j表示Oi,j在Ti,j之前完成).调度目标是使总完工时间tf,max最小.
针对以上问题,作如下假设:1)每台机床的缓冲区均足够大;2)搬运设备一次只能搬运一个工件;3)搬运设备在两台机床之间的搬运时间只取决于机床的位置,与工件无关;4)tk,hL表示负载搬运设备从Mk到Mh的时间,运输时间满足约束关系tk,hL+th,lL≥tk,lL;5)tk,hE表示空载搬运设备从Mk到Mh的时间,空载时间满足约束关系tk,hE+th,lE≥tk,lE,tk,kE=0;6)不考虑工件的加载和卸载时间.
为了清晰地表述调度问题,定义以下符号和变量:tf,i表示工件Ji的完成时间;ts,oi,j表示工序Oi,j开始时间;ts,i,j表示工序Ti,j开始时间;Q为一个任意大的正数;Xj,j′i =1表示Oi,j在Oi,j′之前完成,否则,Xj,j′i =0;DPi,jk = 1表示工序Oi,j由机床Mk完成,否则,DPi,jk=0;YDPi,j,i′,j′k=1表示DPi,jk=1,DPi′,j′k=1且Oi,j先于Oi′,j′在Mk上加工,否则,YDPi,j,i′,j′k = 0; DTi,jR=1表示加工任务Oi,j由搬运设备R运送至下一个对应的加工机床,否则,DTi,jR=0;YDTi,j,i′,j′R=1表示Ti,j先于Ti′,j′被R搬运,否则,YDTi,j,i′,j′R =0.
由上述假设可得如下约束关系:
ts,oi,j+pi,j≤ts,oi′,j′ ,(1)
当两个工序Oi,j和Oi′,j′共用一台机床时,约束关系可表示为

工序Ti,j和Ti′,j′共用搬运设备R搬运,约束关系可表示为

搬运设备要有足够的时间完成两个连续搬运任务,约束关系可以表示为

调度目标为

本文的调度问题是以式(8)为目标,以式(1)~式(7)为约束条件的非线性规划问题.
为了更清晰表述上述调度问题,对析取图模型进行改进,利用G=(Nm∪Nt,C∪Dm∪DR)进行建模.Nm表示加工工序对应的节点集合;Nt表示搬运工序对应的节点集合;C是连接弧集合,表示工序顺序;析取边Dm表示在同一台机床上完成的工序之间的约束关系;析取边DR表示搬运工序之间的约束关系.
加工工序节点指向运输工序节点的弧的权值为加工工序的加工时间.运输节点指向加工节点的弧的权值为运输时间.析取边Dm转为有向弧之后,权值等于有向弧始端的工序的加工时间,析取边DR转为有向弧之后,权值计算见图 1.
 | 图 1 运输节点之间析取弧权值 Fig. 1 The weight of the disjunctive arc between transportation nodes |
析取子图[9]是从析取全图中分离出来的图形,可以更清晰地表述子问题.用M0表示已调度的机床集合,初始值为空集,M表示所有机床集合,SG(m)表示机床m的析取子图,AS(m)表示析取子图SG(m)中所有节点集合,US(m)表示SG(m)中未调度节点集合,URS(m)表示SG(m)中可以调度的节点集合,S(m)表示SG(m)中已经调度的节点集合.用最长路径算法计算各节点的投放时间 ri,j和工期di,j,ti,j表示节点的实际开始加工时间,tf,i,j表示完成时间.
定理1 调度析取子图SG(m)时,如果优先调度的节点Oi,j满足ri,j≥minoi′,j′∈US(m)(max(ti′,j′,ri′,j′)+pi′,j′),则析取子图的最大完工时间tf,max会增加.
证明:设Oi′,j′是使不等式右侧式子值最小的节点,Oi,j满足ri,j≥max(ti′,j′,ri′,j′)+pi′,j′.
若优先调度Oi,j,易知ti,j=ri,j,tf,i,j=ri,j+pi,j.因为ri,j≥max(ti′,j′,ri′,j′)+pi′,j′,所以tf,i,j>ri′,j′,ti′,j′=tf,i,j,tf,i′,j′=ti′,j′+pi′,j′=ri,j+pi,j+pi′,j′.故tf,max1 = max(tf,i,j ,tf ,i′,j′) = ri,j + pi,j + pi′,j′ .
若优先调度Oi′,j′,易知,ti′,j′=ri′,j′,tf,i′,j′=ri′,j′+pi′,j′,因为ri,j≥max(ti′,j′,ri′,j′)+pi′,j′,所以ri,j>tf,i′,j′,ti,j=ri,j,tf,i,j=ri,j+pi,j.故tf,max2=max(tf,i,j,tf,i′,j′)=ri,j+pi,j.
显然,tf,max1>tf,max2,即析取子图的最大完工时间tf,max增加.
定理2 调度析取子图SG(m)时,设ri,jd表示当前调度时刻节点Ti,j的动态投放时间,如果优先调度ri,jd最小的节点,则必然能得到可行解.
证明:图 2表示当前状态下的析取子图SG(R)局部简图,当前未调度节点集合为{Ti,j,Ti′,j′+1}.p(0→x→Ti′,j′+1)表示从起点0到节点Ti′,j′+1的所有路径的集合,l(p)表示路径p的长度,ri′,j′+1d=max{l(p)|p∈p(0→x→Ti′,j′+1)}.又因为当前析取子图中,存在路径p(0→Ti,j→Ti,j+1→Ti′,j′→Ti′,j′+1)∈p(0→x→Ti′,j′+1),所以,ri′,j′ +1d≥l(p(0→Ti,j→Ti,j+1→Ti′,j′→Ti′,j′+1))>
 | 图 2 SG(R)局部简图 Fig. 2 Partial diagram of SG(R) |
l(p(0→Ti,j))=ri,jd.所以,若按照ri,jd对节点进行排序,则Ti,j必然排在Ti′,j′+1之前,这样可以避免析取子图中出现环,即必然能得到可行解.
定理3[2] s是一个可行解,最大完工时间为tf,max(s),如果存在另一个可行解s′,有tf,max(s′)<tf,max(s),那么有1)某个机床块中,至少有一个节点排在首节点之前或者在尾节点之后;2)搬运块中至少有两道搬运工序可交换顺序.
基于以上3个定理,构造了两阶段结构式启发式算法,算法构造描述如下.
步骤1 创建析取图并初始化.
步骤2 根据机床总负载 TWL=∑pi,j 从大到小,确定机床调度顺序.
步骤3 按照机床调度顺序,确定机床m的析取子图SG(m).
步骤4 调度SG(m).
1) 初始化US(m)= AS(m),URS(m)=S(m)=ø ;
2) 若S(m)= AS(m) ,则转步骤5,否则,URS(m)={Oi,j|ri,j≤ { max(ti′,j′,ri′,j′)+pi′,j′ ,Oi,j∈ US(m)} ;
{ max(ti′,j′,ri′,j′)+pi′,j′ ,Oi,j∈ US(m)} ;
3) 对URS(m) 中的所有节点,按照di,j 从小到大的顺序进行排列,所得序列中的节点为Oi,j ,更新S(m)=S(m)∪Oi,j,US(m)= US(m)Oi,j,URS(m)=ø ,转步骤4中的2).
步骤5 将析取子图SG(m) 调度结果插入析取图中.
步骤 6&forauL;m′∈{M0-m},若m′上的工序出现在关键路径中,则重新调度m′,如果制造期缩短则更新m′的工序顺序;否则,保持m′的工序顺序不变.
步骤7 如果M0≠M,则转步骤3.
步骤8 基于机床调度结果分离搬运设备析取子图SG(R).
步骤9 调度SG(R).
步骤10 对步骤1~9得到的解s第一层优化.
步骤11 对s第二层优化.
步骤12 算法结束.
3 仿真实验定义 ,其中tf,maxB表示利用文献[9]提出的改进转换瓶颈算法(MSBH)所求得的最大完工时间.
,其中tf,maxB表示利用文献[9]提出的改进转换瓶颈算法(MSBH)所求得的最大完工时间.
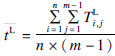 ,tE=(tE-+tE+)/2;Ti,jL表示搬运工序Ti,j的负载运输时间;Ti,jE表示搬运工序Ti,j的空载运输时间;tE-表示空载运输时间可取的最小值;tE+表示空载运输时间可取的最大值;
,tE=(tE-+tE+)/2;Ti,jL表示搬运工序Ti,j的负载运输时间;Ti,jE表示搬运工序Ti,j的空载运输时间;tE-表示空载运输时间可取的最小值;tE+表示空载运输时间可取的最大值;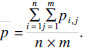 .
.
用m×n×1表示问题规模,参考文献[2, 3]设计4×4×1,6×6×1,10×5×1三种中小规模算例和15×5×1,10×10×1两种大规模算例.4×4×1,6×6×1类算例的加工时间pi,j=[1, 10];10×5×1,15×5×1,10×10×1类算例的pi,j=[1,100].各规模算例的运输时间设置如下:Ti,jL=[0,P],Ti,jE=D|cur-k|.cur表示当前调度时刻搬运设备所处的机床序号;k表示当前调度时刻待搬运工件所处的机床序号;D为空载运输时间系数, .
.
用C++语言编程实现上述算法,并在硬件环境为320 G硬盘、2 GB RAM和2.27 GHz主频intel core(TM) i3处理器的Lenovo笔记本电脑上进行仿真实验.
3.1 问题规模对算法的影响设定pror=0.2,设计各问题规模的实例,实验结果见图 3.
 | 图 3 问题规模对算法运行时间的影响 Fig. 3 Influence of problem scales on algorithm running time |
从图 3可以看出,当pror=0.2时,随着问题规模的增大,Gap值在10%~21%之间波动,趋于平稳.总体来看,算法求解质量相对稳定,且相比文献[9]中的算法优势较显著.
3.2 搬运时间对算法的影响令pror取[0, 1]区间内不同的值,对不同规模的算例进行多次仿真实验,分析搬运时间对算法的影响,见图 4和图 5.
 | 图 4 中小问题规模搬运时间对算法运行时间的影响 Fig. 4 Influence of transporting time in small and medium problem scales on algorithm running time |
 | 图 5 大问题规模搬运时间对算法运行时间的影响 Fig. 5 Influence of transporting time in large problem scales on algorithm running time |
由图 4和图 5可知,随着搬运时间与加工时间的比值pror的增大,Gap值呈减小趋势.当pror小于0.5时,Gap值在5%~20%之间,算法相对文献[9]中的算法的优势比较明显,求解质量较高.当pror大于0.5小于1时,两种算法所求结果的差异较小.实际的生产中,搬运时间一般小于加工时间的50%,即pror小于0.5,因此,本文算法有较高的实用价值.
4 结论1) 在构建数学模型和改进型析取图的基础上,提出的两阶段构造式启发式算法能够有效地求解带物料搬运设备的Job Shop调度问题,为此类问题的调度提供了新思路.
2) 仿真结果表明,当搬运时间与加工时间的比值pror一定时,算法的求解质量相对稳定,并且能够较好地平衡求解质量和求解时间之间的矛盾.
3) 搬运时间与加工时间的比值pror小于0.5时,本文算法与文献[9]的算法的Gap值在5%~20%之间,求解质量明显高于文献[9].
| [1] | Schutten J M J.Practical job shop scheduling[J].Annals of Operations Research,1998,83(2):161-178.( 3) 3) |
| [2] | Hurink J,Knust S.Tabu search algorithms for job-shop problems with a single transport robot[J].European Journal of Operational Research,2005,162(1):99-111.( 3) 3) |
| [3] | 何之洲,杨煜俊,陈新度.带搬运机器人的 job-shop 问题的并行禁忌搜索算法[J].工业工程,2013,16(4):122-125.(He Zhi-zhou,Yang Yu-jun,Chen Xin-du.Parallel tabu search scheduling algorithm for job-shop with transport robot[J].Industrial Engineering Journal,2013,16(4):122-125.)( 2) 2) |
| [4] | 晏鹏宇,车阿大,李鹏,等.具有柔性加工时间的机器人制造单元调度问题改进遗传算法[J].计算机集成制造系统,2010,16(2):404-410.(Yan Peng-yu,Che A-da,Li Peng,et al.Improved genetic algorithm for robotic cell scheduling problem with flexible processing time [J].Computer Integrated Manufacturing Systems,2010,16(2):404-410.)( 1) 1) |
| [5] | Blazewicz J,Pesch E,Sterna M.Application of a modified disjunctive graph for the job shop scheduling problem [C] //Proceedings of the Fourth International Symposium on Methods and Models in Automation and Robotics.Miewdzyzdroje,1997:935-940.( 1) 1) |
| [6] | Lacomme P,Larabi M,Tchernev N.Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles[J].International Journal of Production Economics,2013,143(1):24-34.( 1) 1) |
| [7] | Deroussi L,Gourgand M,Tchernev N.A simple metaheuristic approach to the simultaneous scheduling of machines and automated guided vehicles[J].International Journal of Production Research,2008,46(8):2143-2164.( 1) 1) |
| [8] | Zhang Q,Manier H,Manier M A.A genetic algorithm with tabu search procedure for flexible job shop scheduling with transportation constraints and bounded processing time[J].Computers & Operations Research,2012,39(7):1713-1723.( 1) 1) |
| [9] | Driessel R,Mnch L.An integrated scheduling and material-handling approach for complex job shops:a computational study[J].International Journal of Production Research,2012,50(20):5966-5985.( 1) 1) |




