齿轮是最常用的动力传输和运动传递装置,由于受加工、装配及外界环境等影响,其安装误差、制造误差、外部载荷等因素均具有随机性[1],导致齿轮振动、噪声和点蚀破坏等故障.这些随机因素严重影响齿轮啮合传动的可靠性,然而,常规的齿轮可靠性设计通常将这些随机因素作为固定常量或将其适当简化[2, 3, 4, 5, 6],这样很难准确地进行齿轮可靠性分析.
在齿轮可靠性分析时,由于人力、物力和财力等因素的限制,很难开展真实的可靠性试验来获取大量数据,因此,通过虚拟仿真代替真实响应并与抽样方法相结合来进行可靠性分析已成为可靠性分析方法常用的工具之一.然而即使采用虚拟仿真代替真实响应,由于抽样次数多,也很难在短时间内进行大样本的可靠度计算.基于此,为了解决齿轮接触疲劳可靠性评估计算量大和计算精度低的问题,采用响应面代替真实响应是近几年常采用的方法.
随着现代机械工业技术的发展,要求齿轮传动具有轻型化、高可靠性、高精度等特性,基于此,开展齿轮传动可靠性分析方法的研究,以定量的概率反映安装误差、制造误差及外载荷等随机因素对齿轮传动可靠性的影响程度,对齿轮传动系统的优化设计具有重要意义.
1 可靠性分析方法 1.1 基于响应面的可靠性分析方法为了解决隐式函数关系,常采用响应面法进行可靠性分析.基本思想是采用一系列确定性试验,通过回归分析得到响应面函数,在后续的可靠性分析时采用响应面函数代替系统响应状态函数.根据文献[7],响应面函数的表达式为

根据问题的需要采用一种试验设计(DOE),确定样本点.当随机变量为任意分布时,采用式(2)计算水平点值xn:

当随机变量为正态分布且已知μ和σ分别为均值和标准差时,水平点xn按式(3)确定:

当随机变量为正态分布且已知随机变量的水平点值xn时,变量μ和σ可通过3σ法则将Φ-1(p1)=-3,Φ-1(p2)=0,Φ-1(p3)=3代入式(2)与式(3)得到


对Ns个样本点参数进行仿真计算,得到输出点(y1,y2,…,yNs),采用最小二乘法进行回归分析:

通过求解上述方程组,得到响应面函数式(1)中的系数.之后便可以采用响应面函数替代真实响应以进行可靠性分析.
1.2 MCMC方法马氏链蒙特卡洛(Markov chain Monte Carlo)方法(MCMC法),是一种特殊的蒙特卡洛法.此方法是以平稳分布的马氏链上产生相互依赖的样本,能够模拟出所要求密度函数的样本点.其基本理论框架和更多的基本理论详见文献[8, 9].
在计算失效概率时,通常关心落入失效域的抽样点,因此,本文可靠性算法中,主要是采用MCMC法来模拟失效域的样本点,从这些样本点中筛选出离验算点最近的最佳点,将其加入到试验设计中,建立响应面函数,提高响应面状态函数在失效区域验算点附近的拟合精度,从而提高可靠度的计算精度.设服从在失效域内的条件概率密度函数为q(x|F),则产生失效域F内样本点x(i)(i=1,2,…,N)的具体步骤如下.
1) 定义马尔科夫链的极限(平稳)分布:马尔科夫链的极限分布为失效域F的条件概率密度分布:

2) 选择建议分布f*(ε|x):分布f*(ε|x)是控制马尔科夫链从一个状态向另一个状态的转移,选择具有对称性的均匀分布,即

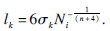 .
.
3) 确定马尔科夫初始链状态x(0):可依据工程经验或数值模拟方法确定失效域内的一点为x(0).
4) 产生马尔科夫链的第j个状态x(j):根据建议分布和Metropolis-Hastings准则,由前一个状态x(j-1)来确定马尔科夫链的第j个状态x(j),即[8]

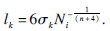 ;random[0,1]为[0,1]区间均匀分布的随机数.
;random[0,1]为[0,1]区间均匀分布的随机数.
5) 产生NM个条件样本点:重复步骤4),当马尔科夫链状态的遍历均值达到稳定后,选取NM个马尔科夫链的状态作为失效域的样本点.图 1为2个不同初始点的4000步迭代的水平转角误差θ遍历均值图.可以看出,到1700步时,迭代得到的马尔科夫链已经基本收敛,只要从收敛后的状态选取NM个样本点即可满足上述要求.

|
图1 4000步迭代的θ遍历均值 Fig. 1 Traversal average value of θ in 4000 iterations |
在经典响应面法的基础上,从这些样本点中筛选出离验算点最近的最佳点,即max(f(xiF))(i=1,2,…,NMC)对应的样本点,将其加入到初始试验设计中,并进行一次动力学仿真,基于更新后的试验设计来建立响应面函数,通过循环迭代提高响应面状态函数在失效区域验算点附近的拟合精度,从而提高可靠度的计算精度.
2 齿轮误差参数化建模与动力学仿真因结构尺寸的变动需要对齿轮模型进行重新建立,费时费力,而齿轮的可靠性分析需要改变参数并重新建模与分析.为了方便快速地进行齿轮可靠度计算和可靠性灵敏度分析,这就要求给定任意齿轮参数,都能够进行动力学仿真并得到应力响应.
2.1 随机变量的考虑研究显示[1],安装误差、制造误差、负载力矩和转速等随机因素对齿轮接触应力有着重要影响,而接触应力是引起齿轮失效的直接原因,故而也是齿轮接触疲劳可靠性分析的主要因素.
根据文献[10, 11],定义安装与制造误差为水平偏移误差Xe、水平转角误差θ、垂直偏移误差Ze、垂直转角误差Φ的合成误差.
齿面的制造误差可将其等效定义为两种偏移的合成,第一种是虚线齿廓①(即理想无误差齿廓)至点划线齿廓②(过渡齿廓)的位置偏移;另一种是由点划线齿廓②至实线齿廓③的形状偏移.
最终主要考虑的随机变量为Xe,Ze,θ,Φ,Δ基节,小齿轮力矩T,大齿轮转速n.其中,齿轮的安装误差Xe,Ze,θ,Φ是根据典型减速器产品中某一齿轮的精度等级和设计指标,通过查取机械设计手册和参考文献[10],根据3σ法则,由式(4)计算得到这些随机变量的均值和标准差数据[7].齿轮的基节误差Δ基节是通过查取机械设计手册得到其均值的最大和最小值,由式(4)可计算得到均值和标准差数据.小齿轮力矩T和大齿轮转速n见文献[7],在试验数据缺乏时取变异系数为0.1.各变量的随机特性如表 1所示[6, 10].
| 表1 各变量的平均值和标准差 Table 1 Mean and standard deviation of different variables |
对于安装误差,按照2.1节所述安装误差的定义,建立基准线,然后在装配齿轮过程中,令齿轮与误差基准线对齐即可.
对于制造误差,根据2.1节的等效定义和文献[11]的方法,把基节偏差值转化为阵列角度偏差,就可以将Δ基节转化为阵列角度偏差:

在阵列齿轮,实际阵列角度为

采用三维建模软件建立含误差的齿轮模型,将式(10)带有偏差齿轮的实际阵列角度设置在Pro/E关系式中,生成带有安装与制造误差的齿轮模型.
2.3 动力学仿真按照2.1节和2.2节的方法建立含有安装与制造误差的齿轮副实体参数化模型,采用大变形非线性显式动力学软件进行仿真[11],模拟含有误差齿轮在啮合过程中的动态接触应力.齿轮副有限元模型见图 2.图 3为大齿轮各随机参数取均值时某一时刻的Von Mises应力云图.

|
图2 齿轮有限元模型 Fig. 2 Finite element model of gear |

|
图3 大齿轮各变量参数取均值时的Von Mises应力云图 Fig. 3 Von Mises stress cloud when variable parameters of gear take the mean |
1) 建立齿面接触疲劳功能函数的基本流程:假设齿面最大接触应力的响应函数为

根据应力-强度模型可知,齿面接触应力大于接触强度,齿面发生点蚀,处于失效状态,故齿面接触疲劳问题的功能函数为

为提高齿面接触疲劳功能函数的拟合精度并进行可靠性分析,本文在响应面法的基础之上,结合MCMC法模拟,提出一种建立响应面功能函数的混合算法.
具体步骤如下:
步骤1 令x1=Xe,x2=Ze,x3=θ,x4=Φ,x5=Δ基节,x6=T,x7=n,选择Box-Behnken[12]作为初始试验设计,设初始样本点为S0=[x(1)x(2)…x(NS)]T,根据2.2节误差齿轮的建模方式建立实体模型,导入到动力学仿真软件中并计算齿轮在啮合过程中齿面最大的接触应力响应,得到齿轮的响应面功能函数值Y0=[y1y2…yNs]T.
步骤2 由S0和Y0,通过最小二乘回归分析法,建立齿面接触疲劳的功能函数,并且令迭代次数Niter为1.
步骤3 根据第1.2节MCMC法模拟当前功能函数失效域内的NMC个样本点,在本文中NMC取1000,设失效域内的样本点为xF(i)(i=1,2,…,NMC)
步骤4 从这些失效域内的NMC个样本点中筛选出max(f(xiF))(i=1,2,…,NMC)对应的样本点,设该样本点为xbest.
步骤5 根据当前的响应面状态函数,采用一次二阶矩法[13]计算设计验算点xNiter*.
步骤6 计算xNiter*与xNiter-1*之间的相对误差是否满足规定的精度误差ε要求,如果xNiter*与xNiter-1*的相对精度误差  小于阀值ε,则停止迭代,说明此时齿面接触疲劳响应面功能函数已达到足够精度;如不满足,令Niter=Niter+1,将xbest加入到S0中来更新试验设计,重新建立响应面功能函数,重复步骤3~步骤6,直至达到精度要求为止.
小于阀值ε,则停止迭代,说明此时齿面接触疲劳响应面功能函数已达到足够精度;如不满足,令Niter=Niter+1,将xbest加入到S0中来更新试验设计,重新建立响应面功能函数,重复步骤3~步骤6,直至达到精度要求为止.
2) 齿面接触疲劳可靠度的计算.按照算法流程编制程序,经过52次循环连续迭代后达到收敛条件,得到满足足够精度的齿面接触疲劳的功能函数,设计验算点x*为[-8.4569,-11.252,-0.00062234,-0.0042345,2.1343,120.7,634.43],可靠度指标β为2.8110,其相对误差小于0.0001,可靠度Φ(β)=0.99753.
表 2为100000次Monte Carlo模拟法、FORM、响应面+FORM法及本文算法的计算结果.其中,100000次Monte Carlo模拟法作为‘精确解’与其他方法比较.
| 表2 不同方法的计算结果 Table 2 Results of different methods |
由表 2可知,FORM采用梯度来迭代寻找设计验算点的方式很难收敛,故而计算结果精度较差.响应面法+FORM法的计算精度有所提高,解决了隐式函数的问题.本文算法在此方法的基础之上,引入了MCMC抽样选点,使得响应面在设计验算点附近更加精确,其计算精度明显高于在未采用MCMC法前的响应面+FORM的计算结果,从而说明了本文算法的高效性和精确性.
3.2 可靠性灵敏度分析各随机参数相互独立,假设均值向量和方差向量为μ=[μ1,μ2,…,μ7]和D=[D1,D2,…,D7],按文献[7]可得

由式(12)~式(16)可得

可靠度指标定义为

如果响应面状态函数g(x)服从正态分布,则可靠度为

因此,可靠度R对基本随机参数矢量的均值矩阵μ和方差D的灵敏度为

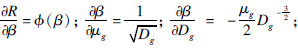
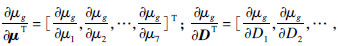
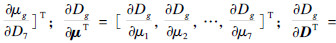
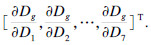
对齿面接触疲劳的功能函数式进行100000次Monte Carlo模拟,可以得到状态函数g(x)的频率直方图和正态概率分布图,分别如图 4和图 5所示.由图 5可知,二者呈直线分布,故认为g(x)服从正态分布.Monte Carlo模拟得到均值与标准差为ug=253.303,σg=88.985.由式(13)~式(18)知,ug=254.556,σg=89.132.上述所得结果与Monte Carlo方法所得数据接近.由式(21),式(22),略去偏导求解过程,得到所有随机变量的可靠性灵敏度为

|
图4 g(x)频率直方图 Fig. 4 Frequency chart of g(x) |

|
图5 g(x)正态概率纸分布图 Fig. 5 Normal probability distribution of g(x) |

由∂R/∂μT所得可靠性灵敏度的结果知,齿面接触疲劳可靠度对转矩T均值灵敏度较强,随着T均值增加而减小,对基节偏差Δ基节和啮合面转角偏差θ均值灵敏度次之,其他所有随机因素均值的影响较小;由∂R/∂DT所得可靠性灵敏度的结果知,T,Δ基节和θ的增加都会降低齿面接触疲劳可靠度.因此,在设计齿轮时需对上述可靠性灵敏度较高的随机因素进行严格控制.
4 结 论1) 本文建立了带有安装与制造误差的齿轮参数化模型,不受误差参数变化的限制,能够实现不同误差齿轮模型的建立,从而为后续的齿面接触疲劳可靠性分析提供了强大的建模基础.
2) 由于引入了MCMC抽样选点,使得响应面在设计验算点附近更加精确,其计算精度明显高于在未采用MCMC法前的响应面+FORM的计算结果,验证了本文算法的高效性,提高了可靠度和可靠性灵敏度的计算精度.
3) 通过100000次Monte Carlo模拟的结果对比可知,本文算法与Monte Carlo较为相近,验证了本文算法的正确性.
| [1] | Ristivojevic M,Lazovic T,Vencl A.Studying the load carrying capacity of spur gear tooth flanks[J].Mechanism and Machine Theory,2013,59(1):125-137.( 2) 2) |
| [2] | Yang Q J.Fatigue test and reliability design of gears[J].International Journal of Fatigue,1996,18(3):171-177.( 1) 1) |
| [3] | Peng X Q,Liu G,Wu L Y,et al.A stochastic finite element method for fatigue reliability analysis of gear teeth subjected to bending[J].Computational Mechanics,1998,21(3):253-261.( 1) 1) |
| [4] | Zhang Y M,Liu Q L,Wen B C,et al.Practical reliability-based design of gear pairs[J].Mechanism and Machine Theory,2003,38(12):1363-1370.( 1) 1) |
| [5] | 李永东,张男,张丙喜,等.某型坦克齿轮接触疲劳强度可靠性的Monte Carlo数值模拟[J].机械强度,2006,28(1):46-50.)(Li Yong-dong,Zhang Nan,Zhang Bing-xi,et al.Numerical simulation for contact fatigue reliability of tank gear by Monte Carlo method[J].Journal of Mechanical Strength,2006,28(1):46-50.)( 1) 1) |
| [6] | 孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京:科学出版社,2003:210-211.)(Sun Zhi-li,Chen Liang-yu.Practical mechanical reliability design theory and method [M].Beijing:Science Press,2003:210-211.)( 3) 3) |
| [7] | 闫明,孙志礼,杨强.基于响应面方法的可靠性灵敏度分析方法[J].机械工程学报,2007,43(10):67-70.(Yan Ming,Sun Zhi-li,Yang Qiang.Analysis method of reliability sensitivity based on response surface methods[J].Chinese Journal of Mechanical Engineering,2007,43(10):67-70.)( 4) 4) |
| [8] | Hastings W K.Monte Carlo sampling methods using Markov chains and their application[J].Biometrika,1970,57(1):97-109.( 2) 2) |
| [9] | Metropolis N,Rosenbluth A W,Rosenbluth M N,et al.Equation of state calculations by fast computing machines [J].The Journal of Chemical Physics,1953,21(6):1087-1092.( 1) 1) |
| [10] | Li S T.Effects of machining errors,assembly errors and tooth modifications on loading capacity,load-sharing ratio and transmission error of a pair of spur gears [J].Mechanism and Machine Theory,2007,42(6):698-726.( 3) 3) |
| [11] | 佟操,孙志礼,马小英,等.考虑安装与制造误差的齿轮动态接触仿真研究[J].东北大学学报(自然科学版),2014,35(7):996-1000.(Tong Cao,Sun Zhi-li,Ma Xiao-ying,et al.Dynamic simulation research of spur gears with assembly errors and machining errors [J].Journal of Northeastern University(Natural Science),2014,35(7):996-1000.)( 3) 3) |
| [12] | Box G,Behnken D.Some new three level designs for the study of quantitative variables[J].Technometrics,1960,2(4):455-476.( 1) 1) |
| [13] | Ditlevsen O,Madsen H O.Structural reliability methods[M].New York:Wiley,1996:87-109.( 1) 1) |
 2016, Vol. 37
2016, Vol. 37
