结合面广泛存在于大量组合机械机构中,结构40%~60%的柔度和90%以上的阻尼是因结合面而产生的[1],研究结合面的动态特性在理论和实际应用上都有很重要的意义.
在实际工程机构中,结合面不可能完全光滑,因此,有必要对结合面的静摩擦系数进行研究.长期以来,众多学者对此进行了大量的探索研究.根据GW模型[2],Chang等[3]经过研究,得到了一种用于计算结合面静摩擦系数的模型.盛选禹等[4]根据M-B分形理论[5],给出了预测静摩擦系数的一种方法.经典的GW模型因受仪器分辨率和采样长度的限制,所以有一定的局限性,而M-B分形模型的建立则弥补了这些.但是,传统的M-B分形模型,没有对微凸体的弹塑性变形进行考虑,认为微凸体的变形是由弹性变形直接过渡到塑性变形.有文献对微凸体的变形进行了研究,发现微凸体的变形过程是从弹性变形过渡到弹塑性变形,最后过渡到塑性变形,并不是从弹性变形直接到塑性变形[6].而在单个微凸体的变形的过程中,弹塑性变形还是占有一定比例的.因此,在建立结合面静摩擦系数的分形模型时,考虑微凸体的弹塑性变形,就显得十分重要.
基于赫兹接触理论和传统的M-B分形接触模型,本文引入微凸体的弹塑性变形,建立了结合面静摩擦系数分形模型.为了清楚地揭示引入微凸体弹塑性变形对结合面静摩擦系数的影响,本文在不考虑弹塑性变形的情况下,建立了结合面静摩擦系数分形模型.并利用仿真软件对这两种模型进行了比较.同时,得到了各相关参数对结合面静摩擦系数的影响.
1 M-B分形接触修正模型在无摩擦情况下,赫兹理论指出两个粗糙面在受载荷Q作用时,接触的模型可以用一个刚性平面与一个粗糙平面接触来简化表示.简化之后的模型如图 1所示.

|
图1 等效球体单峰与刚性平面接触示意图 Fig. 1 The contact diagram of equivalent sphere single peak and rigid plane |
依据赫兹接触理论,当平面压力作用的时候,发生弹性变形微凸体的弹性变形量为

式中:pm表示作用在微凸体上的平均接触压力;E表示等效弹性模量,并且有E=[(1-ν12)/E1 +(1-ν2 2)/E2 ]-1,E1,E2分别为图 1中两弹性体的弹性模量,ν1,ν2分别为两弹性体的泊松比;等效单峰曲率半径R=[1/R1+1/R2]-1,其中,R1,R2分别为两弹性体的曲率半径.
1.1 微凸体的接触状态与相应的接触载荷根据文献[7]可得微凸体的曲率半径为

式中:S为实际接触面积;G为分形尺度参数;D为分形维数.
Johnson理论[8]表明,当接触面积满足β=Er/σyπ=30时( ,为接触半径),微凸体将会产生塑性变形.由Johnson理论和公式(2)可得到临界弹塑性接触面积为
,为接触半径),微凸体将会产生塑性变形.由Johnson理论和公式(2)可得到临界弹塑性接触面积为

微凸体弹性临界变形面积为[8]

式中:φ=σy/E表示材料的特性参数;kμ表示摩擦力修正因子,当0≤μ≤0.3时,kμ=1-0.228μ,当0.3<μ≤0.9时,kμ=0.932e-1.58(μ-0.3).
1) 当Sl<Spt时,微凸体处于塑性接触,受到的载荷为[7]

式中,K为与硬度H和屈服强度σy相关的系数,三者的关系为H=Kσy.
2) 当Spt<Sl<Sc时,微凸体处于弹塑性接触,受到的载荷为

3) 当Sl>Sc,微凸体处于弹性接触,受到的载荷可以表达为[7]

根据M-B分形模型,最大接触面积为Sl与接触点的面积分布n(S)的关系为

式中:ψ为与分形维数D有关的分形区域扩展系数,可以查表得到;Sl则是单个微凸体的最大接触面积.
整个接触面的实际接触面积Ar包含有塑性接触面积、弹塑性接触面积和弹性接触面积.

当不考虑弹塑性变形时,微凸体的变形只分为塑性变形和弹性变形.
当Sl>Sc,1<D<2并且D≠1.5时,不考虑弹塑性变形的法向总载荷可以表示为

式中: ;
;

当Sl>Sc并且D=1.5时,不考虑弹塑性变形的法向总载荷可以表示为

当对微凸体的弹塑性变形进行考虑时,微凸体的变形则分为塑性变形、弹塑性变形和弹性变形.
当Sl>Sc,1<D<2并且D≠1.5时,考虑弹塑性变形的法向总载荷可以表示为

式中:
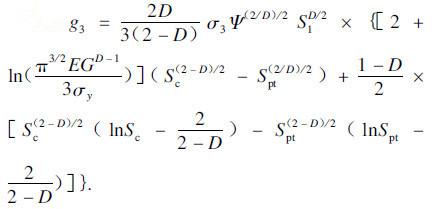
当Sl>Sc并且D=1.5时,考虑弹塑性变形的法向总载荷可以表示为

当微凸体已经发生塑性变形时,在作用法向载荷的情况下,会产生塑性流动,就没有承受切向载荷的能力.所以,在计算微凸体切向载荷的时候,就没有必要考虑塑性变形阶段[9].
3.1 未考虑弹塑性变形结合面切向载荷分形模型当1<D<2并且D≠1.5时,未考虑弹塑性变形的微凸体,弹性阶段的切向载荷为

式中:
当D=1.5时,未考虑弹塑性变形的微凸体,弹性阶段的切向载荷为

对于未考虑弹塑性变形的切向总载荷可以表示为

当1<D<2时,考虑弹塑性变形的微凸体,弹塑性阶段的切向载荷为

考虑弹塑性变形时,切向总载荷可以表示为

当结合面有相对滑动趋势时,处于弹性变形和弹塑性变形的微凸体将发生完全屈服,因而,最大静摩擦力就可以用切向总载荷Q来表达.
因此,未考虑弹塑性变形的结合面静摩擦系数可以表示为

同理,考虑弹塑性变形的结合面静摩擦系数也被得到.
当1<D<2且D≠1.5时:

当D=1.5时:

式中:Q′*=Q′/AaE;P′*=P/AaE;A*r=Ar/Aa;
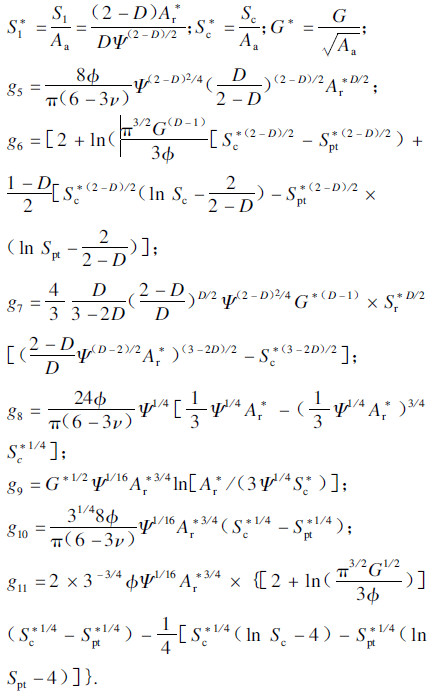
由于篇幅有限,本文仅对考虑弹塑性变形时,结合面静摩擦系数与各参数之间的非线性关系进行了仿真分析.
5.1 分形维数和法向载荷对静摩擦系数的影响根据式(20)和式(21),当K=2.8,φ=1.0,G=1.0×10-10,D分别取1.1~1.9,对静摩擦系数与法向载荷的关系进行仿真,结果如图 2所示.

|
图2
分形维数和法向载荷对静摩擦系数的影响
Fig. 2 Influence of fractal dimension and normal load on static friction coefficient
(a)—D=1.1~1.3; (b)—D=1.3~1.5; (c)—D=1.5~1.7; (d)—D=1.7~1.9. |
图 2表明,结合面的静摩擦系数与法向载荷呈正相关,这与文献[2, 4]的结论相同.当1.1≤D≤1.5,结合面的静摩擦系数与分形维数呈正相关;当1.5≤D≤1.9,结合面静摩擦系数与分形维数呈负相关.
5.2 分形尺度参数对静摩擦系数的影响当K=2.8,φ=1.0时,对静摩擦系数与分形尺度参数的关系进行仿真,仿真结果如图 3所示.

|
图3 分形尺度参数对静摩擦因数的影响曲线 Fig. 3 Influence of fractal scale parameters on static friction coefficient (a)—D=1.3; (b)—D=1.7. |
图 3表明,结合面静摩擦系数与分形尺度参数呈负相关.这与文献[5]的结论是一致的.因为分形尺度参数G*越小,结合面间粗糙度就越小.
5.3 材料特性参数对静摩擦系数的影响取K=2.8,G*=1.0×10-10,D=1.9,φ分别取0.01,0.1,1.0时,对结合面静摩擦系数与材料特性参数的关系进行仿真,结果如图 4所示.

|
图4 材料特性参数对静摩擦因数的影响曲线 Fig. 4 Influence of material parameters on static friction coefficient |
图 4表明,结合面的静摩擦系数与材料特性参数呈正相关.
5.4 弹塑性变形对结合面静摩擦系数影响的对比根据式(19)、式(20)和式(21),当K=2.8,φ=1.0,G=1.0×10-10时,未考虑弹塑性变形与考虑弹塑性变形的结合面静摩擦系数的仿真结果的对比,如图 5所示.

|
图5
弹塑性变形对静摩擦系数的影响曲线
Fig. 5 Influence of elastic-plastic deformation on static friction coefficient
(a)—D=1.3; (b)—D=1.6; (c)—D=1.8; (d)—D=1.9. |
从图 5可以看出,弹塑性变形对结合面的静摩擦系数有影响.但是,影响比较小,这主要是因为弹塑性接触区域所占的比例小.相比于未考虑弹塑性变形的情况,考虑弹塑性变形的结合面静摩擦系数更大.
6 结 论1) 弹塑性变形影响结合面静摩擦系数分形模型的建立.考虑弹塑性变形的结合面静摩擦系数要大于未考虑弹塑性变形的结合面静摩擦系数.
2) 结合面静摩擦系数与法向载荷和材料特性参数呈正相关,而与分形尺度参数呈负相关.分形维数对结合面静摩擦系数的影响比较复杂,当1.1≤D≤1.5时,结合面静摩擦系数与分形维数呈正相关;当1.5≤D≤1.9时,结合面静摩擦系数与分形维数呈负相关.
| [1] | Ren Y,Beards C F.Identification of effective linear joints using coupling and joint identification techniques[J].ASME Journal of Vibration and Acoustics,1998, 120(2):331-338.( 1) 1) |
| [2] | Greenwood J A,Williamson J B P.Contact of nominally flat surfaces[J].Proceeding of the Royal Society of London:A,1966,295(1442):300-319.( 2) 2) |
| [3] | Chang W R,Etsion I,Bogy D B.Static friction coefficient model for metallic rough surfaces[J].ASME Journal of Tribology,1988,110(1):57-63.( 1) 1) |
| [4] | 盛选禹,雒建斌,温诗铸,等.基于分形接触的静摩擦系数预测[J].中国机械工程,1998,9(7):16-18.(Sheng Xuan-yu,Luo Jian-bin,Wen Shi-zhu,et al.Fractal prediction model for static friction coefficient of joint surfaces [J].Journal of Chinese Mechanical Engineering,1998,9(7):16-18.)( 2) 2) |
| [5] | Majumdar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces [J].ASME Journal of Tribology,1991,113(1):1-11.( 2) 2) |
| [6] | Wang S,Komvopoulos K.A fractal theory of the interfacial temperature distribution in the slow sliding regime:part I-elastic contact and heat transfer analysis[J].ASME Journal of Tribology,1994,116(6):812-823.( 1) 1) |
| [7] | 李小彭,赵光辉,梁亚敏,等.两圆柱体结合面法向刚度分形预估模型及其仿真分析[J].农业机械学报,2013,44(10): 277-281.(Li Xiao-peng,Zhao Guang-hui,Liang Ya-min,et al.Fractal prediction model for normal contact stiffness of cylinders joint surface and its simulation analysis[J].Journal of Agricultural Machinery,2013,44(10):277-281.)( 3) 3) |
| [8] | Johnson K L.Contact mechanics[M].Cambridge:Cambridge University Press,1985.( 2) 2) |
| [9] | Kogut L,Etsion I.A semi-analytical solution for the sliding inception of a spherical contact[J].ASME Journal of Tribology,2003,125(3):499-506.( 1) 1) |
 2016, Vol. 37
2016, Vol. 37
