自20世纪初以来,国内外诸多学者针对齿轮传动的承载特性、功率特性、传动效率及可靠性等进行了系统的研究,文献[1-3]在空间曲线/曲面共轭基本原理的基础上对不同类型齿轮的齿面方程进行了详细的理论推导,并对点接触条件下的齿面接触应力、应变等进行了讨论.文献[4-5]对不同齿形的齿轮副接触情况进行了分析、对比.文献[6-8]在平面圆柱齿轮的基础上提出了定轴和不定轴的非圆齿轮副,并对其齿面方程进行了简单推导.文献[9-11]结合面齿轮和非圆齿轮的优势,建立了端曲面齿轮副的相关理论并对其传动比特性进行了详细研究.由于齿轮副仅在节曲线处为纯滚动,因此在轮齿啮合的整个过程中齿面之间存在相对滑移.文献[12-13]建立了含滑移摩擦的接触刚度模型,验证了摩擦系数对接触特性的影响,文献[14]则分析了齿面摩擦对振动特性的影响,但都没有对滑移特性及其影响因素进行分析.
本文在分析凸轮副和常规齿轮副传动原理的基础上,提出了端曲面齿轮副的通用设计方法,并结合齿轮啮合原理和空间坐标变换理论,建立了端曲面齿轮副的运动特性函数、齿面方程和齿面滑移模型.以二阶椭圆端曲面齿轮副为例,对齿面滑移速度及其影响因素进行分析,通过实验验证了齿轮副设计方法和齿面滑移模型的正确性.
1 复合运动凸轮副传动原理在图 1所示端面凸轮机构中,固定坐标系OC-XCYCZC,ON-XNYNZN分别与端面凸轮和圆柱滚子的回转中心固连.其中,端面凸轮为主动轮,圆柱滚子与凸轮在接触点P处作纯滚动的伴随运动.

|
图 1 端面凸轮模型 Fig.1 Theoretical model of face cam 1—端面凸轮; 2—圆柱滚子 |
在运动过程中,端面凸轮回转中心OC位置固定,圆柱滚子在转动的同时具有轴向移动.在某一瞬时t,P点在凸轮和滚子上的速度为

|
(1) |
式中:ωC, ωN分别为端面凸轮和圆柱滚子的角速度;vP-C, v′P-C分别为端面凸轮、圆柱滚子上P点的转动速度; vP-N为圆柱滚子上P′点的移动速度, vP-N为圆柱滚子上P′点的复合速度.由式(1)可知轴线固定的端面凸轮仅有转动, 而圆柱滚子的运动由转动和移动组成, 因此可以实现单输入多输出的复合输出形式.
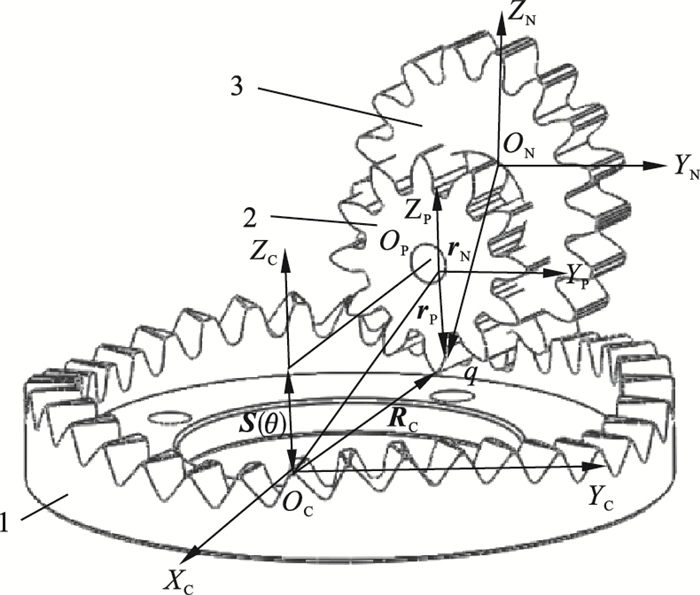
2 端曲面齿轮副齿面设计 2.1 节曲面设计以式(1)所示复合运动方程为基础,结合端曲面齿轮转角θ和传动特性函数f(θ)=S(θ)+i(θ),可建立一非圆齿轮与端曲面齿轮构成的定轴传动齿轮副,其中,S(θ)为位移函数,i(θ)为传动比函数.端曲面齿轮副模型如图 2所示,q为啮合点.记C,P,N分别为端曲面齿轮、主动齿轮和非圆齿轮的固定坐标系;记C′, P′, N′分别对应于三个齿轮的随动坐标系.
|
图 2 端曲面齿轮副模型 Fig.2 3D model of curve face gear pair 1—端曲面齿轮;2—主动齿轮;3—非圆齿轮 |
由图 2所示的位置关系可得非圆齿轮半径rN与端曲面齿轮半径RC的关系为rN+RC=C,同时非圆齿轮的半径rN、主动齿轮半径rP和端曲面齿轮位移S(θ)的关系为

|
(2) |
为简便起见,以下内容中ri, Ri, ωi均为ri, Ri, ωi的模,i=P, N, C.
结合式(1)可知式(2)中端曲面齿轮的位移由端曲面齿轮相对主动轮齿轮的位置变化
在图 2所示的端曲面齿轮副中,主动齿轮的移动速度仅由主动齿轮相对端曲面齿轮的位置函数


|
(3) |
因此在端曲面齿轮副的设计过程中只需满足

|
即可得到满足给定传动特性函数f(θ)=S(θ)+i(θ)的主动齿轮半径rP和端曲面齿轮半径S(θ)-rP.
2.3 齿面方程由齿轮副的可拆分性,根据展成原理结合图 2所示主动齿轮与非圆齿轮刀具的位置关系,得到非圆齿轮和主动齿轮的转动矩阵分别为

|
其中θP和θN分别为主动齿轮和非圆齿轮转角.非圆齿轮固定坐标系与主动齿轮固定坐标系的相对位置矩阵为

|
其中L为非圆齿轮与主动齿轮的中心距,λN为主动齿轮转角.
将刀具齿轮齿廓方程代入主动齿轮的齿面求解方程,结合转动矩阵MNN′,MPP′和移动矩阵MNP得到

|
(4) |
同理,由齿轮啮合原理和空间坐标变换得到端曲面齿轮齿面方程为

|
(5) |
其中θq为主动轮转角.将齿轮副的设计参数代入式(4)或式(5),即可得到对应齿轮的理论啮合齿面.由于端曲面齿轮副在实现给定位移函数的过程中的传动比和位移速度均与节曲线有关,其位移特性S(θ)和转动特性i(θ)不是相互独立的量,需要根据应用场合对二者进行权衡,在满足第一条件的情况下尽量改善第二条件的特性,以期实现给定传动特性函数f(θ).特别地,普通面齿轮副和变传动比定轴端曲面齿轮副的设计仅考虑传动比函数,忽略位移函数的要求;而凸轮副的设计仅考虑位移函数,弱化传动比函数.
3 滑移速度分析 3.1 齿面滑移模型由于端曲面齿轮副在传动过程中既有相对转动又有相对移动,因此其齿面间的相对滑移特性复杂且不能忽略.为简化分析又不失一般性,以二阶椭圆端曲面齿轮副为例分析其啮合过程中的齿面滑移特性,圆柱齿轮为主动齿轮.根据齿轮传动原理和正确啮合条件,建立端曲面齿轮副齿面滑移模型如图 3所示.

|
图 3 端曲面齿轮副齿面滑移模型 Fig.3 Tooth surface sliding model of curve face gear pair (a)—齿面滑移模型;(b)—齿宽平面速度关系. |
坐标系OP-XPYPZP为啮合点处的随动坐标系.引入假想啮合椭圆齿轮后,端曲面齿轮副的复杂空间啮合关系可以简化为端曲面齿轮与椭圆齿轮的空间定轴传动和椭圆齿轮与圆柱齿轮的平面不定轴传动.此时,圆柱齿轮的位移可由图 2所示的非圆齿轮与圆柱齿轮的位置关系表示如下:

|
(6) |
式中:θN为非圆齿轮转角;E为端曲面齿轮与非圆齿轮的中心距;r(θN)为非圆齿轮在转角为θN处的瞬时节圆半径.
将位移对椭圆齿轮转角θN求一阶微分,得到圆柱齿轮的移动速度为

|
(7) |
式中:r′(θN)为非圆齿轮在转角为θN处的瞬时节圆半径的一阶导数.
由式(7)可知,圆柱齿轮相对椭圆齿轮的移动由两部分组成:沿椭圆齿轮半径法向的移动和半径切向的移动,其中法向分量改变移动速度的大小,切向分量仅改变移动速度的方向;特别地,当椭圆齿轮半径固定时,仅有法向的方向变化,速度大小恒为0,即常规定传动比圆柱齿轮副无相对移动.
3.2 相对滑移速度根据式(4)得到圆柱齿轮齿面上啮合点q′处的坐标方程为

|
(8) |
式中:θoq′为圆柱齿轮齿廓起始角;θq′为圆柱齿轮齿廓齿形角;uq′为圆柱齿轮齿宽;rbq′和rq′分别为圆柱齿轮基圆半径和节圆半径.
因此,圆柱齿轮齿面上的啮合点q′相对于端曲面齿轮的啮合点q的运动方程为

|
(9) |
由式(9)结合式(1)和图 3,啮合点q处的速度为

|
(10) |
式中:ω1,ω2和ω3分别为圆柱齿轮、端曲面齿轮和非圆齿轮的转速;i23和i13为端曲面齿轮与非圆齿轮、圆柱齿轮的传动比;rp,rp′分别为端曲面齿轮和圆柱齿轮齿面啮合点向径;vq,vq′分别为端曲面齿轮和圆柱齿轮齿面上啮合点处的瞬时速度.
根据齿廓啮合基本定理,在啮合过程中无齿面脱离和重叠,因此有相对速度vq,vq′在齿面啮合点的公法线方向上的分量相等,对式(10)化简得到

|
(11) |
式中:αqr,αqt和αC是各速度矢量与公法线的夹角,如图 3b所示; vi是vi的模, i=q, T, C.


将齿面方程(4)和(5)与αqr和αqt代入式(10),化简后得到相对速度值为

|
(12) |
式中:vqq′为端曲面齿轮和圆柱齿轮在啮合点处的相对速度.
由上式可知,端曲面齿轮齿面上不同啮合点处的相对滑移速度大小和方向均与转速和移动速度有关.
3.3 滑移特性分析由式(7)和式(12)可知,端曲面齿轮副的传动比和相对移动速度受到齿轮副基本参数的影响,表 1是该齿轮副的部分参数.
| 表 1 端曲面齿轮副部分参数 Table 1 Parameters of curve face gear pair |
在端曲面齿轮副啮合过程中,针对端曲面齿轮不同参数(偏心率、位移、阶数、转速等)作出其半个周期内连续5齿齿面上的相对滑移速度,如图 4~图 6所示.

|
图 4 半周期内滑移速度变化特性 Fig.4 Characteristics of sliding velocity in a half cycle |

|
图 5 轮齿参数对滑移特性的影响 Fig.5 Surface sliding with different parameters |

|
图 6 齿面滑移方向 Fig.6 Direction of surface sliding |
从图 4中可以看出,端曲面齿轮半周期内,每齿的转角范围不同;其中轮齿1和轮齿5的转角略小于同等齿数条件下的转角;轮齿3的转角最大,略大于同等齿数条件下的转角.轮齿1和5的滑移速度整体小于轮齿3的滑移速度,结合式(7)可知,当啮合处于轮齿3所在角度范围时,圆柱齿轮的位移速度最大;对比轮齿5和3的滑移速度,可知在端曲面齿轮半个周期内,轮齿3的传动精度最低,啮合性能最差.
图 5为轮齿1(端曲面齿轮波谷处)轮齿参数对齿面滑移速度的影响.由图可知,端曲面齿轮副阶数的改变对滑移周期的影响最大,阶数越小,滑移速度的变化周期越长.偏心率主要影响端曲面齿轮滑移速度的波动性,偏心率越小,滑移速度波动越小;同样地,转速主要影响齿面滑移速度的平均值,转速越大,式(12)中转速分量越大,齿面滑移速度也越大.
如图 6所示,端曲面齿轮齿面上实际啮合线会由于滑移特性的存在而产生位移,且不同齿高上的相对滑移速度和滑移量的大小不等、方向不同.当端曲面齿轮副处于低速啮合时,齿面主要沿圆柱齿轮的移动方向滑移,而由图 2所示端曲面齿轮的节曲线特性可知,齿面滑移相对端曲面齿轮齿面有向齿宽外侧偏移的分量, 因此,滑移啮合线位于纯滚动啮合线的右上侧.
4 实验验证根据端曲面齿轮副的上述运动特性,搭建相应试验台来验证其滑移特性和位移规律.端曲面齿轮位移规律和齿面滑移特性如图 7所示.

|
图 7 相对位移及滑移速度对比 Fig.7 Comparison of relative displacement and velocity (a)—相对位移对比;(b)—齿面滑移速度对比. |
对比图 7所示的实验和理论的位移曲线、滑移速度曲线发现,该端曲面齿轮副能够较好地实现预期位移特性函数.
根据式(13)对测得的位移数据和角度数据进行二次处理,得到啮合点处滑移速度的实验值.

|
(13) |
结合图 7b可得,实验滑移速度小于理论值且波动明显;波动范围同样具有周期性,在端曲面齿轮节曲线的波谷和波峰位置具有波动极大值10%.考虑到端曲面齿轮副的加工精度、测量方式和安装误差等因素,并对比半个周期内滑移速度的变化趋势依然可以验证滑移速度理论计算的正确性.
5 结论1) 针对复合运动端曲面齿轮副验证了其具有的可变移动特性和传动比特性.并结合齿轮啮合原理和空间坐标变换理论提出了给定运动特性函数下的端曲面齿轮副节曲线通用设计方法;基于齿轮副的可拆分性,建立了端曲面齿轮和主动齿轮的齿面方程.
2) 以椭圆非圆齿轮节曲线为给定位移特性函数,建立了端曲面齿轮副.并结合齿廓啮合基本定理和齿面正确啮合条件,建立端曲面齿轮副齿面滑移模型,推导齿面滑移方程.通过具体参数讨论了不同轮齿和不同参数下的滑移特性,揭示了端曲面齿轮阶数、转速以及位移对滑移速度的影响规律,得到正确啮合条件下轮齿3上的滑移速度及滑移量最大,啮合特性最差.
3) 常规面齿轮副可以看作是端曲面齿轮副给定位移函数为零,传动比函数为定值的特例.因此,本文提出的端曲面齿轮副扩充了齿轮副的节曲线形式,为齿轮副的反求设计提供了理论基础.
| [1] |
Litvin F L, Fuentes A.
Gear geometry and applied theory[M]. New York: Cambridge University Press, 1994: 1374-1576.
|
| [2] |
Litvin F L, Gonzalev-Perez I, Fuentes A, et al.
Design, generation and stress analysis of face-gear drive with helical pinion[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(36/37/38): 3870–3901.
|
| [3] |
吴训成, 胡宁, 陈志恒.
准双曲面齿轮点接触齿面啮合分析的理论公式[J]. 机械工程学报, 2005, 41(6): 81–85.
( Wu Xun-cheng, Hu Ning, Chen Zhi-heng. Theoretical formulae for the meshing analysis of point-contact tooth surfaces of hypoid gears[J]. Journal of Mechanical Engineering, 2005, 41(6): 81–85. DOI:10.3321/j.issn:0577-6686.2005.06.016 ) |
| [4] |
He C J, Lin C.
Analysis of loaded characteristics of helical curve-face gear[J]. Mechanism and Machine Theory, 2017, 115: 267–282.
DOI:10.1016/j.mechmachtheory.2017.05.014 |
| [5] |
Hsu R H, Su H H.
Tooth contact analysis for helical gear pairs generated by a modified hob with variable tooth thickness[J]. Mechanism and Machine Theory, 2014, 71: 40–51.
DOI:10.1016/j.mechmachtheory.2013.09.001 |
| [6] |
Zheng F Y, Lin H, Han X H.
The mathematical model and mechanical properties of variable center distance gears based on screw theory[J]. Mechanism and Machine Theory, 2016, 101: 116–139.
DOI:10.1016/j.mechmachtheory.2016.03.005 |
| [7] |
Zheng F Y, Lin H, Han X H, et al.
Linkage model and manufacturing process of shaping non-circular gears[J]. Mechanism and Machine Theory, 2016, 96(1): 192–212.
|
| [8] |
Xia L, Liu Y Y, Li D Z, et al.
A linkage model and applications of hobbing non-circular helical gears with axial shift of hob[J]. Mechanism and Machine Theory, 2013, 70: 32–44.
DOI:10.1016/j.mechmachtheory.2013.07.002 |
| [9] |
Lin C, Hou Y J, Gong H.
Design and analysis of transmission mode for high-order deformed elliptic bevel gears[J]. Chinese Journal of Mechanical Engineering, 2011, 47: 131–139.
|
| [10] |
Lin C, Zeng D.
Design, generation and tooth width analysis of helical curve-face gear[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2015, 9(5): 1–13.
|
| [11] |
Lin C, He C J.
Analysis of tooth contact and transmission errors of curve face gear[J]. Journal of Mechanical Engineering Science, 2017, 231(19): 3579–3589.
DOI:10.1177/0954406216648354 |
| [12] |
马登秋, 侯力, 魏永峭, 等.
基于分形理论的圆弧齿轮滑移摩擦接触力学模型[J]. 机械工程学报, 2016, 52(15): 121–127.
( Ma Deng-qiu, Hou Li, Wei Yong-qiao, et al. Sliding friction contact mechanics model of the involute arc cylindrical gear based on fractal theory[J]. Journal of Mechanical Engineering, 2016, 52(15): 121–127. ) |
| [13] |
刘鹏, 陈奇, 樊浩, 等.
考虑摩擦的球面切向接触刚度分形模型研究[J]. 中国机械工程, 2016, 20(27): 2773–2778.
( Liu Peng, Chen Qi, Fan Hao, et al. Research on fractal model of TCS between spherical surfaces considering friction factors[J]. China Mechanical Engineering, 2016, 20(27): 2773–2778. ) |
| [14] |
李晓贞, 朱如鹏, 李政民卿, 等.
齿面摩擦对面齿轮传动系统振动特性的影响分析[J]. 振动工程学报, 2014, 27(4): 583–588.
( Li Xiao-zhen, Zhu Ru-peng, Li Zheng-min-qing, et al. Influences of frictional coefficient on vibration characteristic of face-gear transmission system[J]. Journal of Vibration Engineering, 2014, 27(4): 583–588. DOI:10.3969/j.issn.1004-4523.2014.04.014 ) |
 2019, Vol. 40
2019, Vol. 40
