2. 山东大学 机械工程国家级实验教学示范中心, 山东 济南 250061
2. National Engineering Experimental Teaching Demonstration Center of Mechanical Engineering, Shandong University, Jinan 250061, China
近年来, 四足机器人的奔跑研究日益引起许多学者的关注.高速奔跑能力将极大提高机器人在搜救、探险、军用等方面的应用价值.而具有柔性脊椎的四足机器人的奔跑运动分析, 作为仿生机器人研究的一部分, 将推动机器人学、仿生学等多方面的研究[1-10].
麻省理工学院仿生学机器人实验室设计的MIT cheetah机器人具有差分式柔顺仿生脊柱和骨骼肌腱杆件腿结构, 通过差分器控制脊椎的上下弯曲, 并将脊椎弯曲与髋关节转动耦合, 可实现22 km/h的高速奔跑[11].德黑兰大学的Khoramshahi等设计了一款具有柔性脊椎的四足机器人, 其脊椎为一旋转关节, 可上下旋转35°.实验发现柔性脊椎可增大前后腿摆动幅度, 提高运动速度[12].
为提高奔跑性能, 本文设计了一种具有柔性脊椎的四足机器人, 其腿部采用缓冲结构.分析了此柔性脊椎模型对于奔跑步长的影响, 采用基于Hopf模型的CPG生物控制方法对机器人进行bound步态的仿真, 证实了具有柔性脊椎的四足机器人奔跑性能可显著提高.
1 四足机器人结构设计仿生四足动物, 设计一种具有柔性脊椎和缓冲腿结构的四足机器人, 如图 1所示.
|
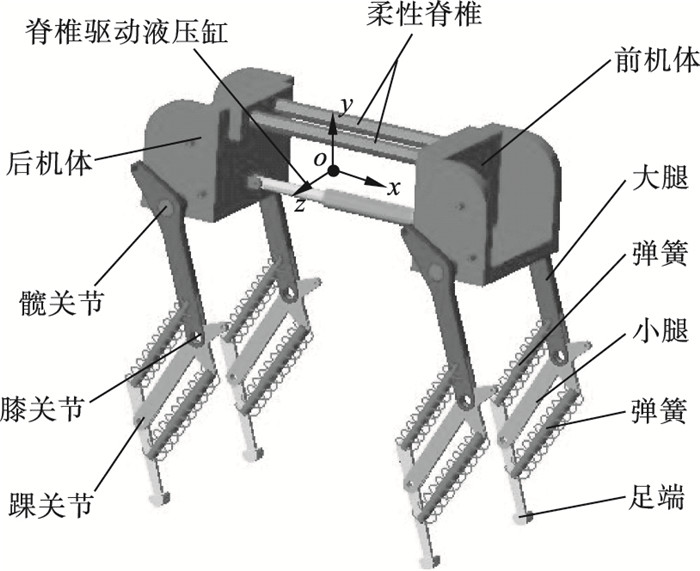
图 1 柔性脊椎四足机器人模型 Fig.1 Quadruped robot model with the flexible spine |
四足机器人机体包括前机体和后机体两个部分, 前机体和后机体由柔性脊椎及其驱动液压缸连接.柔性脊椎由两根有弹性的橡胶棒组成, 两根橡胶棒平行固定在前机体和后机体上.柔性脊椎正下方有一个驱动液压缸, 该液压缸的伸缩可使脊椎上下弯曲.
四足机器人腿部为缓冲式腿结构, 每条腿具有3个自由度, 即髋关节的俯仰自由度、膝关节的俯仰自由度和踝关节的俯仰自由度.其中踝关节为被动关节.此腿结构的详细描述和分析见文献[2], 在此不再重复.四足机器人整体长0.95 m, 宽0.45 m, 高0.95 m, 脊椎长0.55 m, 总重约85 kg.四足机器人机体坐标系见图 1.
2 柔性脊椎对奔跑步长的影响分析为了提高四足机器人的奔跑性能, 采用柔性脊椎有助于增大机器人奔跑时的步长和提高机器人奔跑的稳定性.图 2为四足机器人bound步态奔跑的示意图.

|
图 2 四足机器人bound步态奔跑示意图 Fig.2 Running diagram of the quadruped robot with bound gait |
当脊椎驱动液压缸缩短时, 柔性脊椎会向上弯曲.当脊椎驱动液压缸伸长时, 柔性脊椎会向下弯曲.柔性脊椎的上下弯曲使前机体和后机体的位姿变化, 从而导致足端的落足点位置产生变化, 最终使步长增加.
下面推导步长的增加量.
图 3为柔性脊椎向上弯曲示意图, 可用于推导脊椎驱动液压缸伸缩量ΔL和前机体(后机体)转角的关系.在初始状态下, 两根橡胶棒平行固定在前机体和后机体上, 且呈直线状平行于地面.此时, 驱动液压缸的长度与两根平行橡胶棒的长度均为L, 橡胶棒在弯曲过程中总长度保持不变.设脊椎弯曲过程中脊椎驱动液压缸长度为L′, 收缩量为ΔL=L-L′, k为初始状态下柔性脊椎和脊椎驱动液压缸之间的竖直距离, α为前机体(后机体)相对于初始位置的转角.奔跑过程中, 四足机器人的柔性脊椎对称弯曲, 在脊椎弯曲挠度较小的情况下, 可将脊椎弯曲近似视为一段圆弧, 半径为R.根据几何关系可得

|
图 3 柔性脊椎向上弯曲示意图 Fig.3 Diagram of the flexible spine upward bending |

|
(1) |
得出脊椎驱动液压缸的伸缩量ΔL和前机体(后机体)转角α的关系如下:

|
(2) |
图 4为前机体转角α对步长增加量S的影响示意图.下面以前腿为例, 推导前机体转角α和步长增加量S的关系.从脊椎上弯到脊椎下弯, 前腿足端在前进方向(x方向)的位移即增加的步长量.图 4a的粗实线表示机器人的初始状态, 图 4a虚线表示机器人脊椎上弯的状态.设从初始状态到脊椎上弯的状态, 脊椎驱动液压缸的伸缩量为ΔL1, 引起的前机体转角为α1; 图 4b粗实线表示机器人的初始状态, 图 4b虚线表示机器人脊椎下弯的状态.设从脊椎初始状态到脊椎下弯状态的脊椎驱动液压缸伸缩量为ΔL2, 引起的前机体转角为α2.

|
图 4 前机体转角对步长影响 Fig.4 Influence of front body angle on step length (a)—脊椎上弯; (b)—脊椎下弯. |
推导四足机器人步长增加量时, 不需考虑腿部关节的转动带来的步长量, 因此可将腿部简化为图 4a的实折线的腿部初始状态和虚折线的脊椎上弯的腿部状态.腿部初始状态的实折线绕点A旋转至脊椎上弯状态的腿部虚折线, A点为脊椎驱动液压缸与前机体的连接点, m为脊椎驱动液压缸与前机体的连接点A至足端的距离.脊椎上弯的过程可看作腿部初始状态在水平方向平移ΔL1, 然后转动α1的结果; 脊椎下弯的过程可看作腿部初始状态在水平方向平移ΔL2, 然后转动α2的结果.
设h为初始状态下点A与足底的垂直高度, S为所求的单腿步长增加量, 推导可得前机体转角α和步长增加量S的关系:

|
(3) |
本文采用基于中枢模式发生器(central pattern generator, CPG)的生物控制方法来实现四足机器人的控制, CPG控制方法的优点在于可以在没有高层控制信号和外部反馈输入的条件下, 能够产生稳定的节律信号, 运动控制简单, 参数易调节[13].CPG是产生节律信号的中心控制单元, 可以通过对中枢模式发生器的建模、多个单元之间的相位耦合以及网络的拓扑结构的改变来实现四足机器人协调运动.
本文选用李华师等改进的Hopf振荡器模型[14], 该模型振荡稳定、参数较少且易调节.由于本文研究内容不涉及与环境的交互, 因此在此模型中不需要引入外部反馈项, 此振荡器模型的数学模型如下:

|
(4) |
式中:i, j为振荡器的序号; x和y为两个互相耦合的输出信号, 可分别作为同一条腿的髋、膝关节的关节驱动信号, 其中, xi通过改变幅值系数、频率直接控制髋关节, yi可通过滤波、改变幅值系数等方法来直接控制膝关节; 该模型极限环的半径及振荡器幅值是

为实现四足机器人腿部和脊椎的协调运动, 设置CPG网络拓扑结构如图 5所示, 其中1号振荡器控制左前腿(LF), 2号振荡器控制右前腿(RF), 3号振荡器控制右后腿(RB), 4号振荡器控制左后腿(LB), 5号振荡器控制脊椎, 方形虚线框内表示足间及脊椎间的耦合; 椭圆形虚线内表示足内耦合, 即腿部髋关节和膝关节的信号耦合.

|
图 5 CPG拓扑结构 Fig.5 CPG topological structure |
腿部的三个关节中, 踝关节为被动关节, 不添加驱动信号, 髋关节和膝关节驱动信号幅值影响着奔跑的速度以及是否拖地等情况.图 6为一条腿从支撑相到摆动相的摆动示意图, 用于确定腿部髋关节和膝关节的驱动信号幅值.

|
图 6 机器人腿部关节幅值计算示意图 Fig.6 Robot leg joint amplitude calculation diagram |
图 6中, θ1, θ2和θ3为腿部角度的初始值, l1, l2和l3为腿部各腿节的长度.L为腿部初始状态下的长度值, L′为腿部处于支撑相末期的长度, φ为腿部被动踝关节的转动引起的髋关节转动点相对于足端的角度增量值, h为足端最大离地高度, Ah为髋关节摆动角度幅值, Ak为膝关节摆动角度幅值, Aa为踝关节摆动角度幅值, 因踝关节为被动关节, 确定时可视为已知量.
腿部各关节驱动信号的幅值的确定原则如下:
1) 髋关节驱动信号幅值Ah的大小取决于步长S的大小, 根据机体长度和腿长设置合理的步长S, 可得理想的腿部髋关节幅值Ah.
2) 摆动相中间时刻为足端离地最大距离, 此时Ah=0, Ak达到最大, 设置最大离地高度h, 得到腿部膝关节驱动信号幅值Ak.
根据原则1)以及几何关系可得

|
(5) |
其中:

|
根据原则2)得

|
(6) |
最终根据式(5), 式(6)得出

|
(7) |
因此, 根据上述幅值确定方法, 确定出髋膝关节摆动角度幅值, 设置ω=5π, 即T=0.4 s, Aspine的值自行给定, CPG具体网络参数见表 1.
| 表 1 CPG网络参数表 Table 1 Parameters of CPG network |
CPG网络各信号输出曲线如图 7所示, 将各输出曲线直接作为四足机器人bound步态奔跑时各关节的驱动信号.θH, θK分别为各腿髋关节和膝关节角度驱动信号, Aspine为液压缸的伸缩量.

|
图 7 bound步态CPG网络输出信号 Fig.7 Output signal of CPG for bound gait (a)—右后腿关节摆角曲线; (b)—左后腿关节摆角曲线; (c)—左前腿关节摆角曲线; (d)—右前腿关节摆角曲线; (e)—脊椎液压缸伸缩量曲线. |
根据上述CPG控制方法, 利用Adams和MATLAB/simulink对具有柔性脊椎的四足机器人进行bound步态仿真分析.
为了验证柔性脊椎对前向奔跑性能的影响, 同时由于机器人结构左右对称、左右关节驱动信号完全相同, 机器人侧向运动对前向运动影响较小, 因此本文仿真验证只考虑四足机器人在矢状面内柔性脊椎的动态变化, 以及足端在前向和竖直方向的受力情况.
四足机器人整体长0.95 m, 脊椎长0.55 m, 脊椎长度占比约58%, 四足机器人奔跑仿真采用bound步态, 设置驱动液压缸伸缩量为0.1 m.图 8为四足机器人奔跑仿真过程中一个周期内的仿真截图.

|
图 8 机器人bound步态运动仿真 Fig.8 Simulation of the robot moving on the slope with bound gait |
图 9为仿真中四足机器人质心在三个方向上的位移曲线.三条曲线分别表示质心在x(前进方向), y(高度方向), z(横向)三个方向上的位移.由图 9可知, 机器人在1.0 s后奔跑达到稳定状态, 在x方向(前进方向)直线斜率稳定, 表明行进平稳; y方向(高度方向)波动值在0~0.2 m之间周期性波动, 奔跑稳定; z方向(横向)在行进27 m时仅偏移0.3 m, 偏移率为1%.

|
图 9 机器人质心在x, y, z方向的位移 Fig.9 Displacement curves of body mass center in the x, y and z direction |
为比较柔性脊椎和刚性脊椎对四足机器人奔跑速度的影响, 设置两组对照仿真, 分别进行脊椎驱动液压缸的最大伸缩量为0.1 m时的bound步态奔跑仿真和脊椎保持直线的刚性机体模型的bound步态奔跑仿真.
图 10为两组奔跑仿真的机器人质心在前进方向的速度曲线对比.实线为脊椎驱动液压缸的最大伸缩量为0.1 m时的机体质心前进方向的速度曲线, 虚线为脊椎驱动液压缸不动作时(刚性机体)的速度曲线.在各腿部驱动完全相同的情况下, 脊椎为柔性时, 速度可稳定在2.8 m/s, 脊椎为刚性时, 速度大约稳定在1.5 m/s.由此可知, 在脊椎驱动液压缸的最大伸缩量为0.1 m, 即占脊椎原长的18.8%时, 速度提高了86.6%, 柔性脊椎对速度的提高作用显著.

|
图 10 质心在x方向上的速度 Fig.10 Velocity of the mass center in the x direction |
图 11为两组奔跑仿真的机器人前腿足端接触力曲线对比, 实线为驱动液压缸伸缩量为0.1 m时的足端接触力曲线, 虚线为刚性脊椎时的足端接触力曲线.当脊椎由驱动液压缸主动控制弯曲时, 前腿足端接触力保持在750 N左右.当脊椎保持刚性不弯曲时, 前腿足端接触力峰值维持在600 N左右.可见, 柔性脊椎的四足机器人奔跑时足端蹬地力更大, 对于提高机器人的奔跑速度是有利的.

|
图 11 前腿足端接触力 Fig.11 Foot contact force of the front leg |
1) 本文设计了一种柔性脊椎四足机器人结构, 其脊椎由两根平行橡胶棒组成, 通过控制脊椎正下方的液压缸收缩可实现脊椎主动弯曲.
2) 利用基于Hopf模型的CPG控制方法对机器人进行控制, 通过网络拓扑结构的重建将脊椎驱动信号与各腿部关节的驱动信号进行耦合, 并基于此网络模型, 确定了腿部各关节驱动信号的幅值.
3) 分析了柔性脊椎有助于机器人奔跑步长的加大, 推导了机器人前机体转角和步长增加量的关系.
4) 利用Adams和MATLAB/Simulink对机器人进行了bound步态仿真分析, 仿真结果证明了具有柔性脊椎的四足机器人奔跑速度可显著提高且奔跑稳定.
| [1] |
Deng Q, Wang S G, Xu W, et al. Quasi passive bounding of a quadruped model with articulated spine[J]. Mechanism and Machine Theory, 2012, 52: 232-242. DOI:10.1016/j.mechmachtheory.2012.02.003 |
| [2] |
马宗利, 刘永超, 朱彦防, 等. 奔跑四足机器人腿结构设计与分析[J]. 东北大学学报(自然科学版), 2016, 37(9): 1305-1310. (Ma Zong-li, Liu Yong-chao, Zhu Yan-fang, et al. Design and analysis of quadruped robots' structure[J]. Journal of Northeastern University(Natural Science), 2016, 37(9): 1305-1310. DOI:10.3969/j.issn.1005-3026.2016.09.019) |
| [3] |
Wada N, Akatani J, Miyajima N, et al. The role of vertebral column muscles in level versus upslope treadmill walking—an electromyographic and kinematic study[J]. Brain Research, 2006, 1090(1): 99-109. DOI:10.1016/j.brainres.2006.01.132 |
| [4] |
Seok S, Wang A, Michael C M Y, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1117-1129. DOI:10.1109/TMECH.2014.2339013 |
| [5] |
Eckert P, Sprowitz A, Witte H, et al.Comparing the effect of different spine and leg designs for a small bounding quadruped robot[C]//IEEE International Conference on Robotics and Automation(ICRA).Seattle, 2015: 3128-3133.
|
| [6] |
Zhao Q, Ellenberger B, Sumioka H, et al.The effect of spine actuation and stiffness on a pneumatically-driven quadruped robot for cheetah-like locomotion[C]//IEEE International Conference on Robotics and Bio-mimetics(ROBIO).Shenzhen, 2013: 1807-1812.
|
| [7] |
Koco E, Kovacic Z.Multiobjective locomotion optimization of quadruped robot with different 2DOF configurations of actuated spine[C]//IEEE Mediterranean Conference on Control and Automation(MED).Athens, Greece, 2016: 504-511.
|
| [8] |
Lei J T, Yu H Y. Study on the musculoskeletal body for quadruped robots with spinning gait[J]. High Technology Letters, 2015, 21(3): 245-252. |
| [9] |
Semini C, Tsagarakis N G, Guglielmino E, et al. Design of HyQ—a hydraulically and electrically actuated quadruped robot[J]. Proceedings of the Institution of Mechanical Engineers Part Ⅰ:Journal of Systems & Control Engineering, 2011, 225(6): 831-849. |
| [10] |
Gao J Y, Duan X G, Huang Q, et al.The research of hydraulic quadruped bionic robot design[C]//International Conference on Complex Medical Engineering.Beijing, 2013: 620-625.
|
| [11] |
Seok S, Wang A, Chuah M Y, et al.Design principles for highly efficient quadrupeds and implementation on the MIT cheetah robot[C]//IEEE International Conference on Robotics & Automation.Karlsruhe, Germany, 2013: 3307-3312.
|
| [12] |
Khoramshahi M, Sprowitz A, Tuleu A, et al.Benefits of an active spine supported bounding locomotion with a small compliant quadruped robot[C]//IEEE International Conference on Robotics & Automation.Karlsruhe, Germany, 2013: 3329-3334.
|
| [13] |
Wei X, Wei W.Hopf oscillator-based gait transition for a quadruped robot[C]//IEEE International Conference on Robotics & Biomimetics.Bali, Indonesia, 2015: 2074-2079.
|
| [14] |
李华师.四足机器人仿生运动控制理论与方法的研究[D].北京: 北京理工大学, 2014. (Li Hua-shi.Biomimetic locomotion control theories and methods of quadruped robot[D].Beijing: Beijing Institute of Technology, 2014. http://cdmd.cnki.com.cn/article/cdmd-10007-1014086737.htm) |
 2020, Vol. 41
2020, Vol. 41
