
东北大学学报(自然科学版) ›› 2024, Vol. 45 ›› Issue (12): 1706-1716.DOI: 10.12068/j.issn.1005-3026.2024.12.005
• 信息与控制 • 上一篇
收稿日期:2023-06-09
出版日期:2024-12-10
发布日期:2025-03-18
通讯作者:
李占山
作者简介:刘 杰(1973-),女,吉林长春人,吉林大学副教授基金资助:
Jie LIU, Wen-jing TAN, Zhan-shan LI( )
)
Received:2023-06-09
Online:2024-12-10
Published:2025-03-18
Contact:
Zhan-shan LI
摘要:
基于自表示的无监督特征选择能够处理未标记数据且不受伪标签影响.为了令此类方法同时具有良好的鲁棒性、保留样本局部结构、能选出最具代表性的特征,提出了一种新的方法,并设计了一个对应的迭代优化算法来计算其目标函数.该方法先对样本异常值进行识别和处理,然后将传统的自表示模型与非凸稀疏约束和流形正则结合形成目标模型,再将预处理后的数据放入模型进行特征选择,最后使用所选特征进行聚类.将所提方法在9个真实数据集上与7种方法进行对比实验,实验结果表明,所提方法可以有效解决无监督特征选择问题.
中图分类号:
刘杰, 谭文静, 李占山. 基于稀疏自表示及流形正则化的无监督特征选择[J]. 东北大学学报(自然科学版), 2024, 45(12): 1706-1716.
Jie LIU, Wen-jing TAN, Zhan-shan LI. Unsupervised Feature Selection Based on Sparse Self-representation with Manifold Regularization[J]. Journal of Northeastern University(Natural Science), 2024, 45(12): 1706-1716.
| 数据集 | 样本数 | 特征数 | 分类数 |
|---|---|---|---|
| DBworld | 64 | 4 702 | 2 |
| PCMAC | 1 943 | 3 289 | 2 |
| TOX-171 | 1 715 | 748 | 4 |
| lung | 203 | 3 312 | 5 |
| lymphoma | 96 | 4 026 | 9 |
| nci9 | 60 | 9 712 | 9 |
| JAFFE | 213 | 1 024 | 10 |
| warpPIE10P | 210 | 2 420 | 10 |
| Isolet | 1 560 | 617 | 26 |
表1 实验数据集描述
Table1 Description of the experimental dataset
| 数据集 | 样本数 | 特征数 | 分类数 |
|---|---|---|---|
| DBworld | 64 | 4 702 | 2 |
| PCMAC | 1 943 | 3 289 | 2 |
| TOX-171 | 1 715 | 748 | 4 |
| lung | 203 | 3 312 | 5 |
| lymphoma | 96 | 4 026 | 9 |
| nci9 | 60 | 9 712 | 9 |
| JAFFE | 213 | 1 024 | 10 |
| warpPIE10P | 210 | 2 420 | 10 |
| Isolet | 1 560 | 617 | 26 |
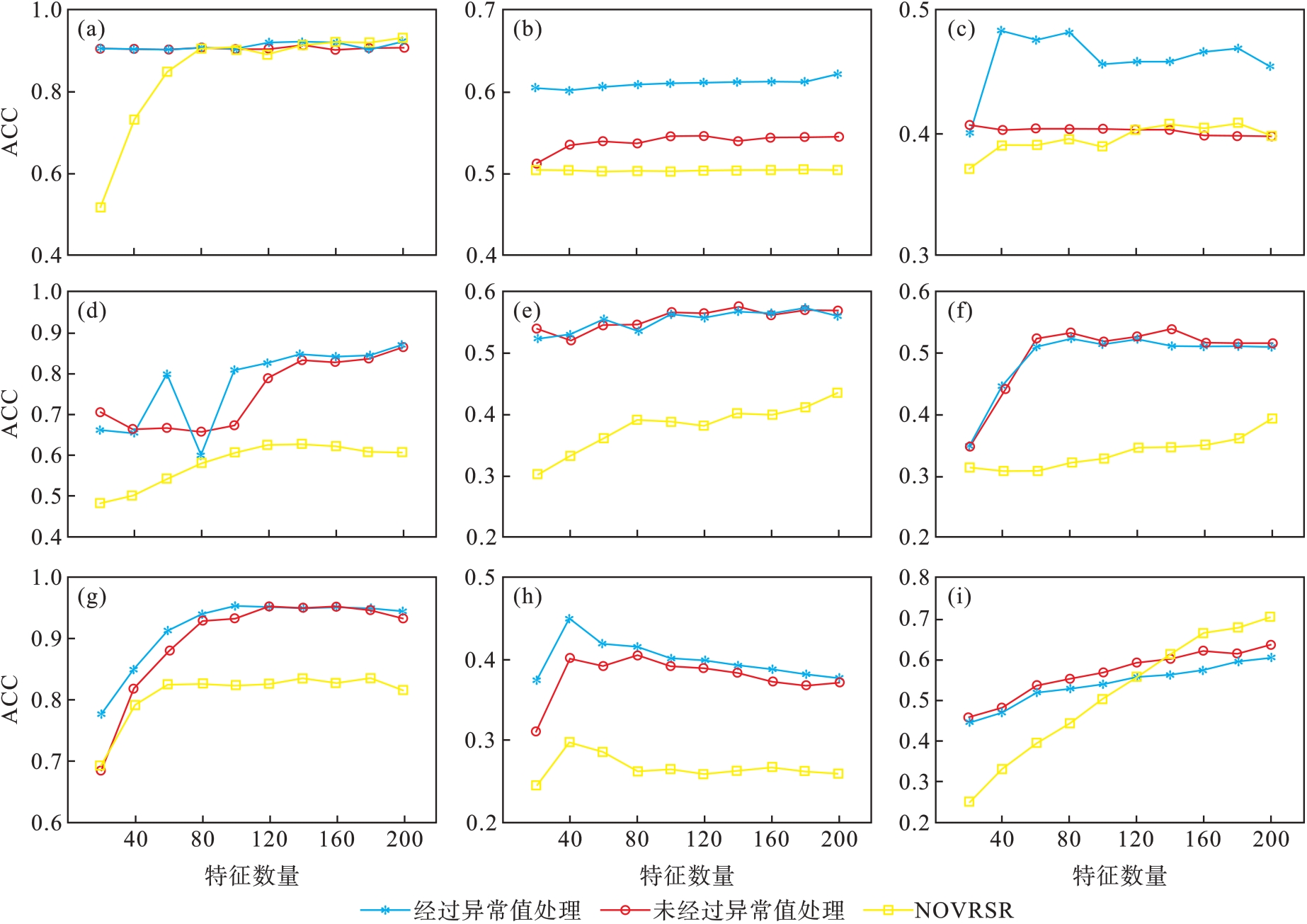
图1 SSRMR和NOVRSR的ACC结果比较(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.1 Comparison of SSRMR and NOVRSR for ACC
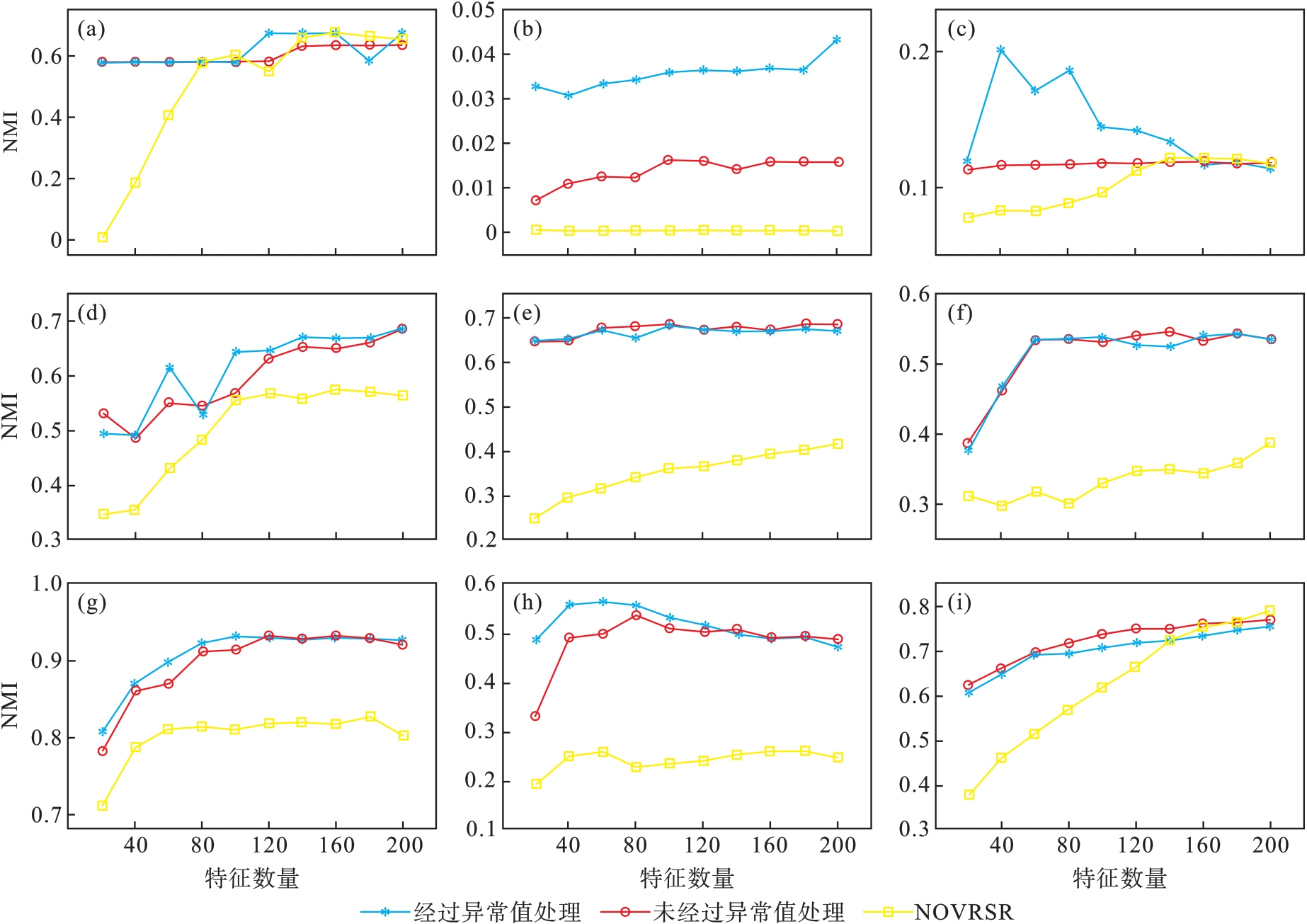
图2 SSRMR和NOVRSR的NMI结果比较(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.2 Comparison of SSRMR and NOVRSR for NMI
| 数据集 | Baseline | LS | MCFS | SPEC | UDFS | RSR | SCFS | NOVRSR | SSRMR |
|---|---|---|---|---|---|---|---|---|---|
| DBworld | 66.953 | 82.891 | 88.047 | 57.344 | 90.703 | 93.516 | 90.938 | 92.188 | |
| ±12.503 | ±4.514 | ±1.584 | ±1.116 | ±0.341 | ±0.558 | ±1.683 | ±0 | ||
| (4702) | (180) | (120) | (200) | (200) | (200) | (200) | (200) | (200) | |
| PCMAC | 50.54 | 50.466 | 50.525 | 55.288 | 50.587 | 50.592 | 50.849 | 62.198 | |
| ±0.033 | ±0.164 | ±0.024 | ±1.077 | ±0.022 | ±0 | ±0 | ±0.104 | ||
| (3289) | (200) | (200) | (60) | (20) | (60) | (200) | (60) | (200) | |
| TOX171 | 42.69 | 40.029 | 41.316 | 42.456 | 41.345 | 41.55 | 46.345 | 53.509 | |
| ±2.661 | ±2.071 | ±0.425 | ±0.726 | ±1.373 | ±1.414 | ±3.537 | ±1.649 | ||
| (5748) | (200) | (20) | (20) | (160) | (100) | (200) | (200) | (100) | |
| lung | 76.626 | 67.4631 | 85.813 | 57.512 | 62.192 | 76.502 | 87.094 | 78.202 | |
| ±6.922 | ±0.802 | ±1.13 | ±3.384 | ±4.975 | ±6.893 | ±0.251 | ±8.175 | ||
| (3312) | (140) | (200) | (180) | (200) | (200) | (180) | (200) | (200) | |
| lymphoma | 59.375 | 53.333 | 61.615 | 46.25 | 58.333 | 54.063 | 65.521 | 60.365 | |
| ±4.576 | ±5.586 | ±3.642 | ±2.244 | ±5.322 | ±2.256 | ±5.511 | ±5.869 | ||
| (4026) | (200) | (60) | (120) | (200) | (180) | (200) | (200) | (160) | |
| nci9 | 43.083 | 40.917 | 43.833 | 40 | 47.333 | 39.417 | 43.833 | 55.333 | |
| ±3.13 | ±3.183 | ±3.617 | ±3.456 | ±2.759 | ±4.058 | ±3.578 | ±3.317 | ||
| (9712) | (140) | (40) | (180) | (20) | (200) | (120) | (200) | (200) | |
| JAFFE | 85.962 | 70.493 | 82.324 | 66.737 | 80.329 | 85.164 | 88.568 | 95.328 | |
| ±2.729 | ±4.223 | ±4.839 | ±4.467 | ±5.596 | ±2.229 | ±2.970 | ±1.201 | ||
| (1024) | (180) | (180) | (200) | (180) | (100) | (160) | (200) | (100) | |
| warpPIE10P | 26.738 | 35.31 | 44.69 | 30.69 | 41.262 | 30.071 | 26.595 | 48.31 | |
| ±2.016 | ±2.627 | ±1.912 | ±2.354 | ±1.834 | ±2.462 | ±1.349 | ±4.223 | ||
| (2420) | (80) | (80) | (200) | (80) | (60) | (20) | (200) | (160) | |
| Isolet | 62.083 | 57.205 | 52.375 | 56.644 | 55.705 | 67.631 | 72.356 | 70.737 | |
| ±2.678 | ±1.759 | ±1.818 | ±2.125 | ±2.385 | ±2.165 | ±2.0 | ±2.132 | ||
| (617) | (200) | (180) | (200) | (200) | (200) | (180) | (200) | (200) |
表2 各数据集上的聚类结果ACC (%)
Table 2 Clustering results ACC on different datasets
| 数据集 | Baseline | LS | MCFS | SPEC | UDFS | RSR | SCFS | NOVRSR | SSRMR |
|---|---|---|---|---|---|---|---|---|---|
| DBworld | 66.953 | 82.891 | 88.047 | 57.344 | 90.703 | 93.516 | 90.938 | 92.188 | |
| ±12.503 | ±4.514 | ±1.584 | ±1.116 | ±0.341 | ±0.558 | ±1.683 | ±0 | ||
| (4702) | (180) | (120) | (200) | (200) | (200) | (200) | (200) | (200) | |
| PCMAC | 50.54 | 50.466 | 50.525 | 55.288 | 50.587 | 50.592 | 50.849 | 62.198 | |
| ±0.033 | ±0.164 | ±0.024 | ±1.077 | ±0.022 | ±0 | ±0 | ±0.104 | ||
| (3289) | (200) | (200) | (60) | (20) | (60) | (200) | (60) | (200) | |
| TOX171 | 42.69 | 40.029 | 41.316 | 42.456 | 41.345 | 41.55 | 46.345 | 53.509 | |
| ±2.661 | ±2.071 | ±0.425 | ±0.726 | ±1.373 | ±1.414 | ±3.537 | ±1.649 | ||
| (5748) | (200) | (20) | (20) | (160) | (100) | (200) | (200) | (100) | |
| lung | 76.626 | 67.4631 | 85.813 | 57.512 | 62.192 | 76.502 | 87.094 | 78.202 | |
| ±6.922 | ±0.802 | ±1.13 | ±3.384 | ±4.975 | ±6.893 | ±0.251 | ±8.175 | ||
| (3312) | (140) | (200) | (180) | (200) | (200) | (180) | (200) | (200) | |
| lymphoma | 59.375 | 53.333 | 61.615 | 46.25 | 58.333 | 54.063 | 65.521 | 60.365 | |
| ±4.576 | ±5.586 | ±3.642 | ±2.244 | ±5.322 | ±2.256 | ±5.511 | ±5.869 | ||
| (4026) | (200) | (60) | (120) | (200) | (180) | (200) | (200) | (160) | |
| nci9 | 43.083 | 40.917 | 43.833 | 40 | 47.333 | 39.417 | 43.833 | 55.333 | |
| ±3.13 | ±3.183 | ±3.617 | ±3.456 | ±2.759 | ±4.058 | ±3.578 | ±3.317 | ||
| (9712) | (140) | (40) | (180) | (20) | (200) | (120) | (200) | (200) | |
| JAFFE | 85.962 | 70.493 | 82.324 | 66.737 | 80.329 | 85.164 | 88.568 | 95.328 | |
| ±2.729 | ±4.223 | ±4.839 | ±4.467 | ±5.596 | ±2.229 | ±2.970 | ±1.201 | ||
| (1024) | (180) | (180) | (200) | (180) | (100) | (160) | (200) | (100) | |
| warpPIE10P | 26.738 | 35.31 | 44.69 | 30.69 | 41.262 | 30.071 | 26.595 | 48.31 | |
| ±2.016 | ±2.627 | ±1.912 | ±2.354 | ±1.834 | ±2.462 | ±1.349 | ±4.223 | ||
| (2420) | (80) | (80) | (200) | (80) | (60) | (20) | (200) | (160) | |
| Isolet | 62.083 | 57.205 | 52.375 | 56.644 | 55.705 | 67.631 | 72.356 | 70.737 | |
| ±2.678 | ±1.759 | ±1.818 | ±2.125 | ±2.385 | ±2.165 | ±2.0 | ±2.132 | ||
| (617) | (200) | (180) | (200) | (200) | (200) | (180) | (200) | (200) |
| 数据集 | Baseline | LS | MCFS | SPEC | UDFS | RSR | SCFS | NOVRSR | SSRMR |
|---|---|---|---|---|---|---|---|---|---|
| DBworld | 17.375 | 44.727 | 47.326 | 2.479 | 63.825 | 56.353 | |||
| ±15.971 | ±6.811 | ±4.008 | ±0 | ±0.882 | ±5.407 | ||||
| (4 702) | (120) | (120) | (40) | (200) | (160) | (200) | (160) | (200) | |
| PCMAC | 0.008 | 1.381 | 0.471 | 2.033 | 6.926 | 0.03 | 0.104 | 1.592 | |
| ±0.011 | ±0.236 | ±0 | ±0 | ±1.382 | ±0.016 | ±0 | ±0 | ||
| (3 289) | (80) | (80) | (60) | (20) | (60) | (200) | (20) | (40) | |
| TOX171 | 14.688 | 12.98 | 9.874 | 10.148 | 13.272 | 12.177 | 23.294 | 31.578 | |
| ±2.74 | ±0.921 | ±0.034 | ±0.971 | ±0.762 | ±0.987 | ±7.503 | ±0.512 | ||
| (5 748) | (200) | (20) | (20) | (180) | (140) | (200) | (200) | (200) | |
| lung | 65.168 | 53.709 | 67.189 | 45.702 | 50.832 | 60.323 | 70.218 | 63.707 | |
| ±2.776 | ±0.9 | ±1.793 | ±4.042 | ±2.446 | ±2.805 | ±0.351 | ±2.07 | ||
| (3 312) | (140) | (200) | (200) | (200) | (180) | (180) | (200) | (200) | |
| lymphoma | 69.043 | 58.015 | 47.799 | 65.767 | 66.604 | 70.126 | 69.171 | 71.931 | |
| ±3.416 | ±3.49 | ±3.515 | ±4.057 | ±1.985 | ±3.126 | ±3.523 | ±2.616 | ||
| (4 026) | (120) | (200) | (120) | (160) | (180) | (180) | (200) | (200) | |
| nci9 | 44.395 | 41.921 | 45.858 | 41.222 | 39.115 | 50.2 | 44.908 | 56.22 | |
| ±3.41 | ±3.811 | ±3.146 | ±2.96 | ±2.84 | ±2.0 | ±3.086 | ±2.949 | ||
| (9 712) | (160) | (60) | (180) | (20) | (200) | (120) | (200) | (200) | |
| JAFFE | 86.014 | 69.179 | 85.84 | 69.808 | 85.426 | 83.381 | 88.24 | 93.202 | |
| ±1.560 | ±2.074 | ±1.601 | ±2.818 | ±1.707 | ±2.019 | ±1.486 | ±1.238 | ||
| (1 024) | (180) | (40) | (200) | (160) | (180) | (160) | (200) | (100) | |
| warpPIE10P | 26.221 | 33.778 | 31.614 | 41.078 | 27.508 | 26.595 | 47.854 | 58.906 | |
| ±3.363 | ±1.906 | ±1.814 | ±2.233 | ±2.584 | ±1.392 | ±1.267 | ±3.268 | ||
| (2 420) | (180) | (80) | (200) | (80) | (180) | (200) | (200) | (160) | |
| Isolet | 77.268 | 73.573 | 69.561 | 66.886 | 71.741 | 79.497 | 79.362 | 80.156 | |
| ±1.288 | ±0.704 | ±1.122 | ±0.703 | ±1.321 | ±1.056 | ±0.807 | ±1.052 | ||
| (617) | (200) | (180) | (200) | (200) | (200) | (180) | (200) | (200) |
表3 各数据集上的聚类结果NMI (%)
Table 3 Clustering results NMI on different datasets
| 数据集 | Baseline | LS | MCFS | SPEC | UDFS | RSR | SCFS | NOVRSR | SSRMR |
|---|---|---|---|---|---|---|---|---|---|
| DBworld | 17.375 | 44.727 | 47.326 | 2.479 | 63.825 | 56.353 | |||
| ±15.971 | ±6.811 | ±4.008 | ±0 | ±0.882 | ±5.407 | ||||
| (4 702) | (120) | (120) | (40) | (200) | (160) | (200) | (160) | (200) | |
| PCMAC | 0.008 | 1.381 | 0.471 | 2.033 | 6.926 | 0.03 | 0.104 | 1.592 | |
| ±0.011 | ±0.236 | ±0 | ±0 | ±1.382 | ±0.016 | ±0 | ±0 | ||
| (3 289) | (80) | (80) | (60) | (20) | (60) | (200) | (20) | (40) | |
| TOX171 | 14.688 | 12.98 | 9.874 | 10.148 | 13.272 | 12.177 | 23.294 | 31.578 | |
| ±2.74 | ±0.921 | ±0.034 | ±0.971 | ±0.762 | ±0.987 | ±7.503 | ±0.512 | ||
| (5 748) | (200) | (20) | (20) | (180) | (140) | (200) | (200) | (200) | |
| lung | 65.168 | 53.709 | 67.189 | 45.702 | 50.832 | 60.323 | 70.218 | 63.707 | |
| ±2.776 | ±0.9 | ±1.793 | ±4.042 | ±2.446 | ±2.805 | ±0.351 | ±2.07 | ||
| (3 312) | (140) | (200) | (200) | (200) | (180) | (180) | (200) | (200) | |
| lymphoma | 69.043 | 58.015 | 47.799 | 65.767 | 66.604 | 70.126 | 69.171 | 71.931 | |
| ±3.416 | ±3.49 | ±3.515 | ±4.057 | ±1.985 | ±3.126 | ±3.523 | ±2.616 | ||
| (4 026) | (120) | (200) | (120) | (160) | (180) | (180) | (200) | (200) | |
| nci9 | 44.395 | 41.921 | 45.858 | 41.222 | 39.115 | 50.2 | 44.908 | 56.22 | |
| ±3.41 | ±3.811 | ±3.146 | ±2.96 | ±2.84 | ±2.0 | ±3.086 | ±2.949 | ||
| (9 712) | (160) | (60) | (180) | (20) | (200) | (120) | (200) | (200) | |
| JAFFE | 86.014 | 69.179 | 85.84 | 69.808 | 85.426 | 83.381 | 88.24 | 93.202 | |
| ±1.560 | ±2.074 | ±1.601 | ±2.818 | ±1.707 | ±2.019 | ±1.486 | ±1.238 | ||
| (1 024) | (180) | (40) | (200) | (160) | (180) | (160) | (200) | (100) | |
| warpPIE10P | 26.221 | 33.778 | 31.614 | 41.078 | 27.508 | 26.595 | 47.854 | 58.906 | |
| ±3.363 | ±1.906 | ±1.814 | ±2.233 | ±2.584 | ±1.392 | ±1.267 | ±3.268 | ||
| (2 420) | (180) | (80) | (200) | (80) | (180) | (200) | (200) | (160) | |
| Isolet | 77.268 | 73.573 | 69.561 | 66.886 | 71.741 | 79.497 | 79.362 | 80.156 | |
| ±1.288 | ±0.704 | ±1.122 | ±0.703 | ±1.321 | ±1.056 | ±0.807 | ±1.052 | ||
| (617) | (200) | (180) | (200) | (200) | (200) | (180) | (200) | (200) |
| 方法 | DBworld | PCMAC | TOX171 | lung | lymphoma | nci9 | JAFFE | warpPIE10P | Isolet |
|---|---|---|---|---|---|---|---|---|---|
| SCFS | 44.337 | 37.518 | 332.559 | 14.911 | 357.831 | 1 413.197 | 1.520 | 15.725 | 3.805 |
| NOVRSR | 13.204 | 234.375 | 722.079 | 180.455 | 291.301 | 3 033.359 | 11.20 | 80.941 | 2.963 |
| SSRMR | 124.265 | 23.767 | 8 707.735 | 80.199 | 10.971 | 148.519 | 2.937 | 3.268 | 45.972 |
表4 不同数据集的运行时间比较 (s)
Table 4 Running time comparison of different methods
| 方法 | DBworld | PCMAC | TOX171 | lung | lymphoma | nci9 | JAFFE | warpPIE10P | Isolet |
|---|---|---|---|---|---|---|---|---|---|
| SCFS | 44.337 | 37.518 | 332.559 | 14.911 | 357.831 | 1 413.197 | 1.520 | 15.725 | 3.805 |
| NOVRSR | 13.204 | 234.375 | 722.079 | 180.455 | 291.301 | 3 033.359 | 11.20 | 80.941 | 2.963 |
| SSRMR | 124.265 | 23.767 | 8 707.735 | 80.199 | 10.971 | 148.519 | 2.937 | 3.268 | 45.972 |
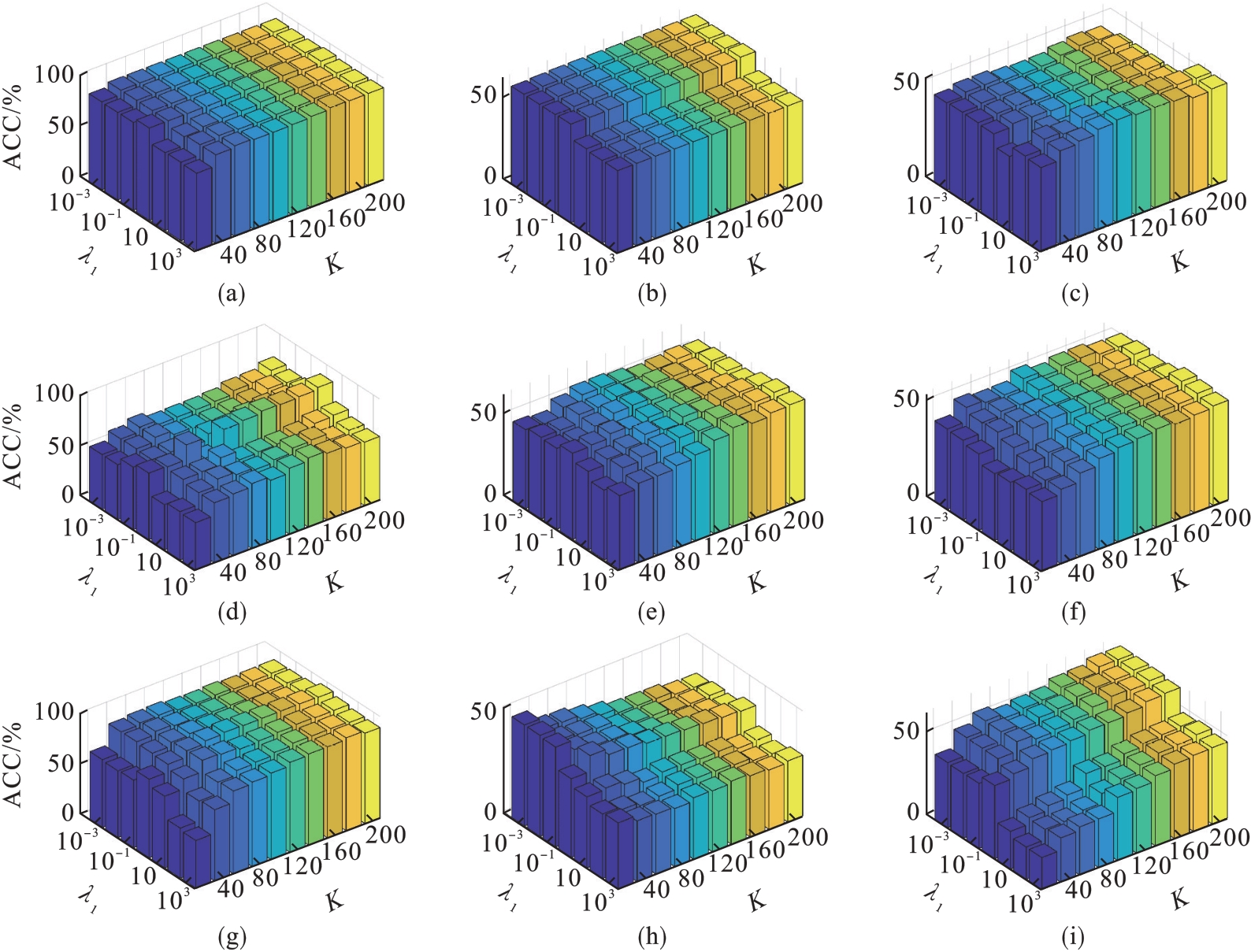
图4 λ1和K的不同取值对ACC的影响(λ2=1)(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.4 Clustering results (ACC) with respect to λ1 and K (λ2=1)
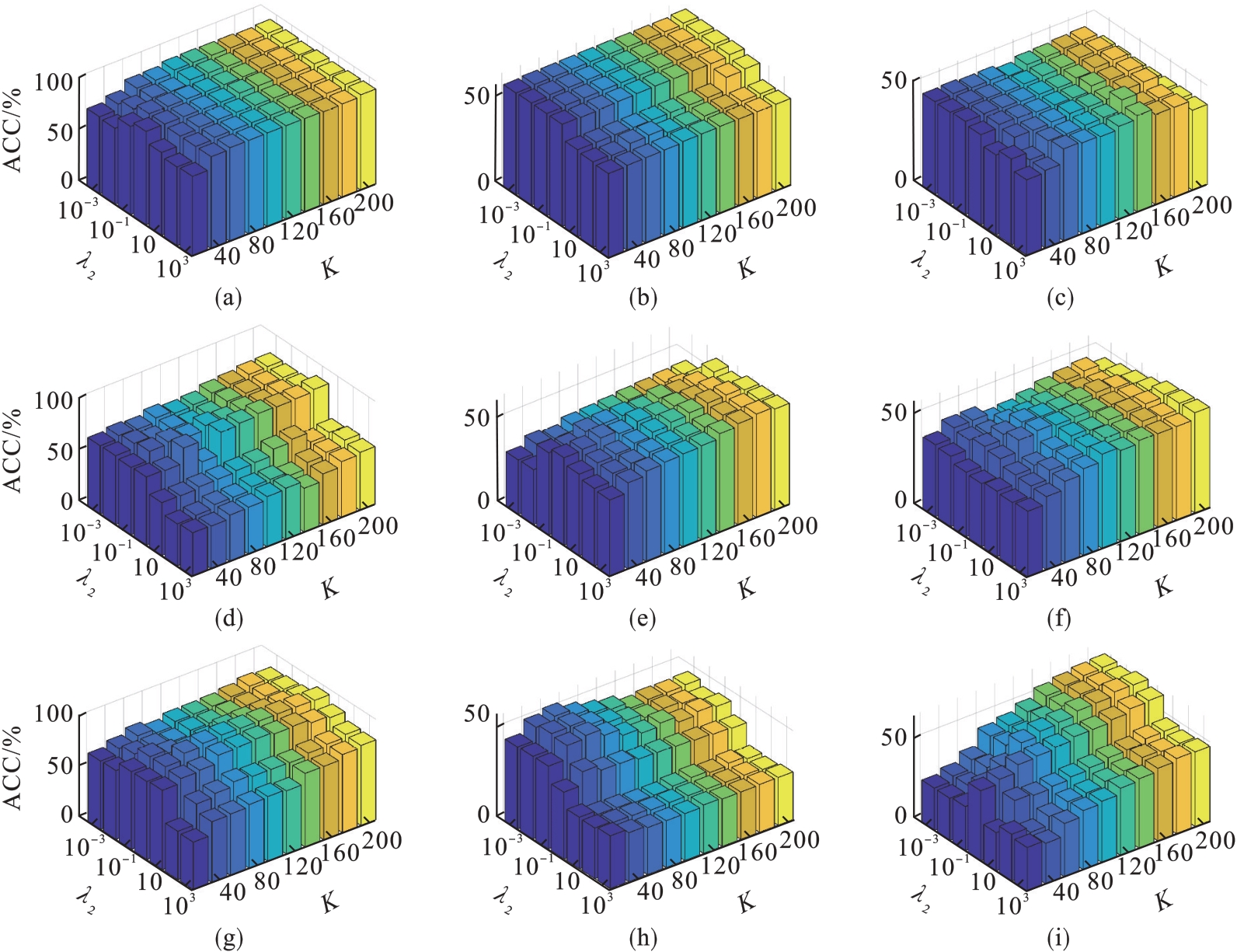
图5 λ2和K的不同取值对ACC的影响(λ1=1)(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.5 Clustering results (ACC) with respect to λ2 and K (λ1=1)
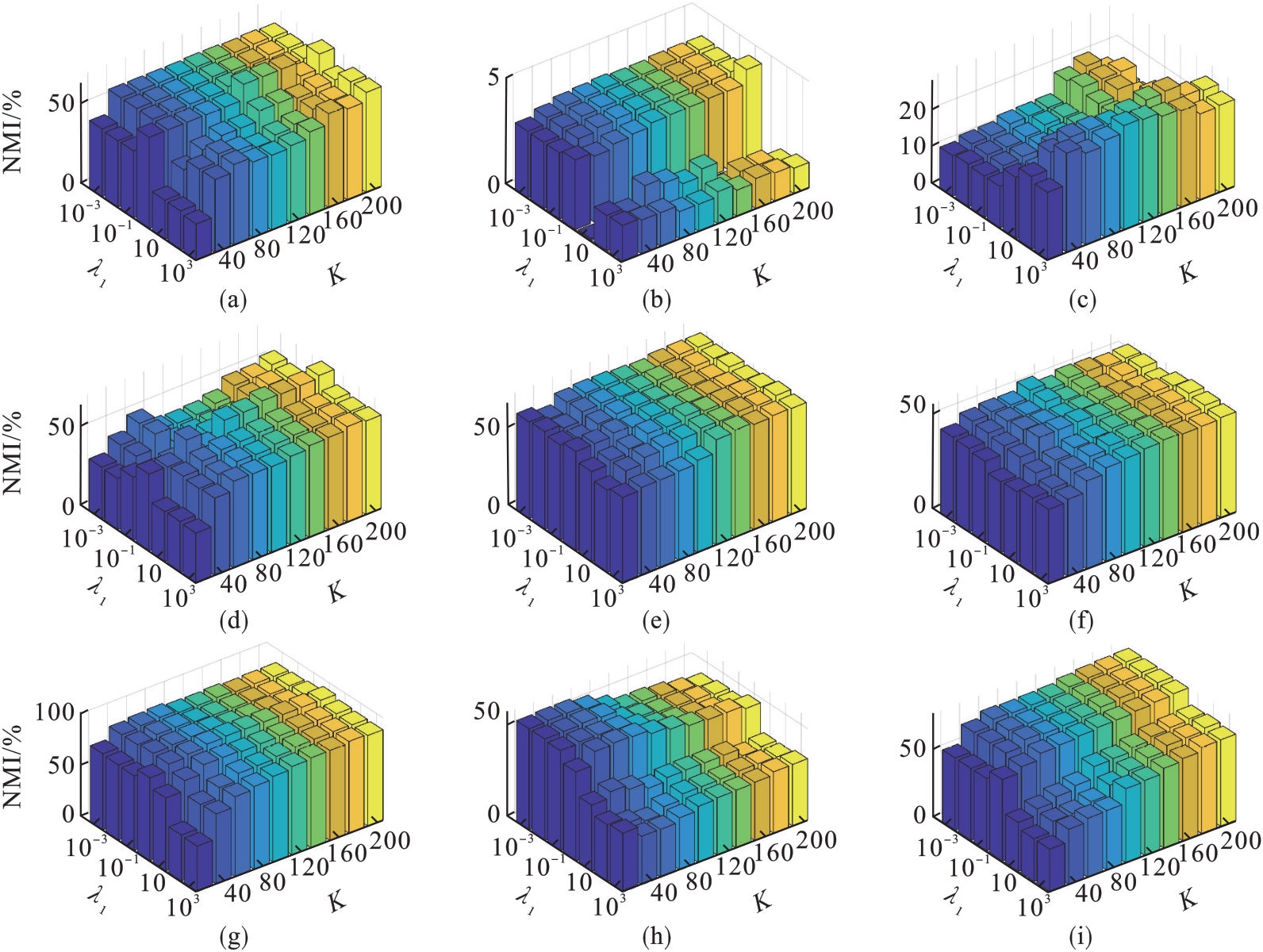
图6 λ1和K的不同取值对NMI的影响(λ2=1)(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.6 Clustering results (NMI) with respect to λ1 and K (λ2=1)
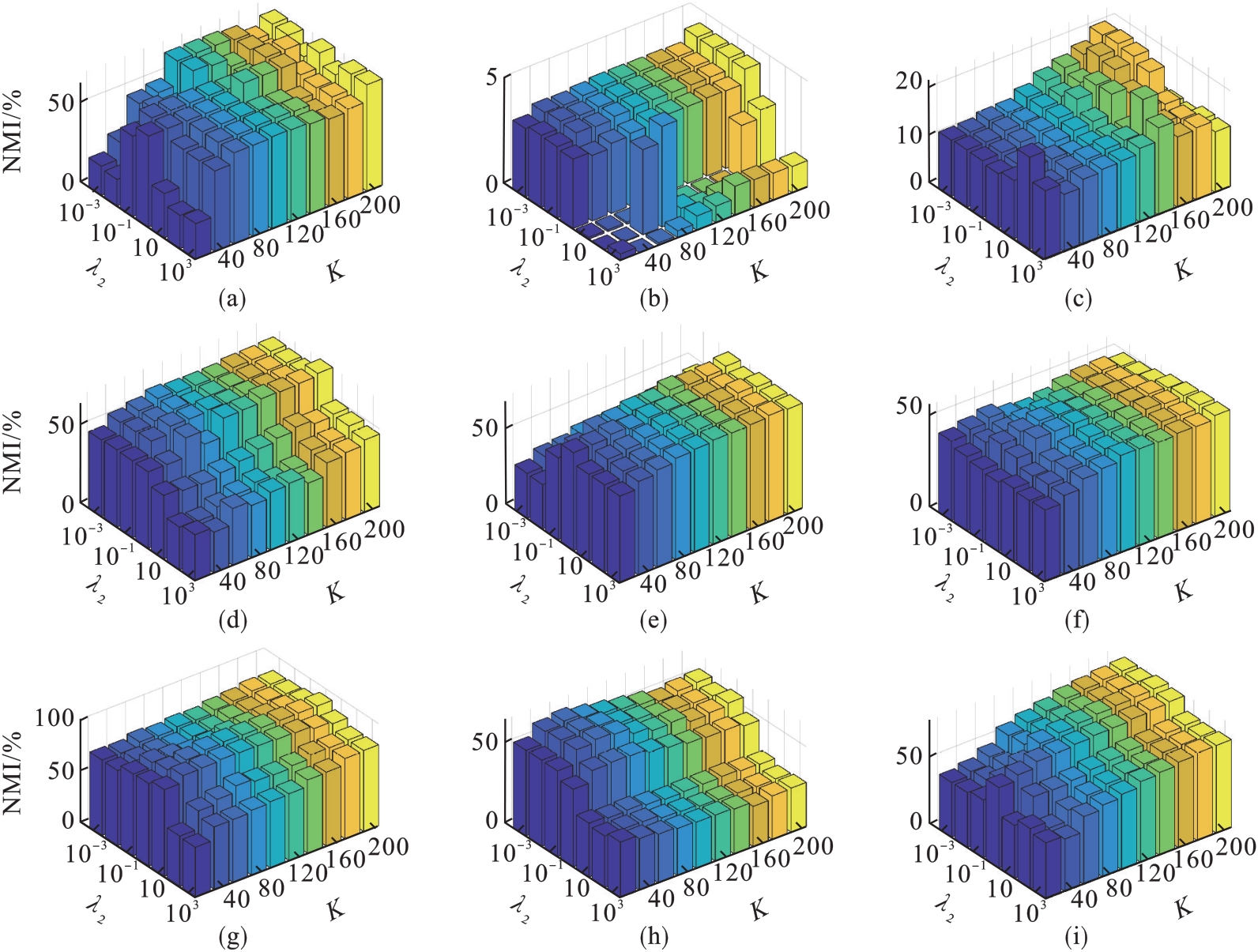
图7 λ2和K的不同取值对NMI的影响(λ1=1)(a)—DBworld; (b)—PCMAC; (c)—TOX171; (d)—lung; (e)—lymphoma;(f)—nci9; (g)—JAFFE; (h)—warpPIE10P; (i)—Isolet.
Fig.7 Clustering results (NMI) with respect to λ2 and K (λ1=1)
| 1 | Solorio‑Fernández S, Ariel J, Martínez‑Trinidad J.A review of unsupervised feature selection methods[J].The Artificial Intelligence Review,2020,53(2):907-948. |
| 2 | He X F, Cai D, Niyogi P.Laplacian score for feature selection[C]// Proceedings of the 18th International Conference on Neural Information Processing Systems.Vancouver,2005:507-514. |
| 3 | Yang Y, Shen H T, Ma Z G,et al .L 2,1‑norm regularized discriminative feature selection for unsupervised learning[C]// Proceedings of the Twenty‑Second International Joint Conference on Artificial Intelligence-Volume Two.Menlo Park:AAAI Press,2011:1589-1594. |
| 4 | Zhao Z, Liu H.Spectral feature selection for supervised and unsupervised learning[C]// Proceedings of the 24th International Conference on Machine Learning.Corvalis,2007:1151-1157. |
| 5 | Cai D, Zhang C, He X F.Unsupervised feature selection for multi‑cluster data[C]// Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Washington DC,2010:333-342. |
| 6 | 李占山,刘兆赓,俞寅,等.量子化信息素蚁群优化特征选择算法[J].东北大学学报(自然科学版),2020,41(1):17-22. |
| Li Zhan‑shaan, Liu Zhao‑geng, Yu Yin,et al.A quantized pheromone ant colony optimization algorithm for feature selection[J].Journal of Northeastern University(Natural Science),2020,41(1):17-22. | |
| 7 | Hu R Y, Zhu X F, Cheng D B,et al.Graph self‑representation method for unsupervised feature selection[J].Neurocomputing,2017,220:130-137. |
| 8 | Nie F P, Zhu W, Li X L.Unsupervised feature selection with structured graph optimization[C]//Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence.Phoenix,2016:1302-1308. |
| 9 | Lim H, Kim D.Pairwise dependence‑based unsupervised feature selection[J].Pattern Recognition,2021,111:107663. |
| 10 | Liu X W, Wang L, Zhang J,et al.Global and local structure preservation for feature selection[J].IEEE Transactions on Neural Networks and Learning Systems,2013,25(6):1083-1095. |
| 11 | Li W Y, Chen H M, Li T R,et al.Unsupervised feature selection via self‑paced learning and low‑redundant regularization[J].Knowledge‑Based Systems,2022,240:108150. |
| 12 | Parsa M, Zare H, Ghatee M.Unsupervised feature selection based on adaptive similarity learning and subspace clustering[J].Engineering Applications of Artificial Intelligence,2020,95:103855. |
| 13 | Zhu P F, Zuo W M, Zhang L,et al.Unsupervised feature selection by regularized self‑representation[J].Pattern Recognition,2015,48(2):438-446. |
| 14 | Miao J Y, Ping Y, Chen Z S,et al.Unsupervised feature selection by non‑convex regularized self‑representation[J].Expert Systems with Applications,2021,173:114643. |
| 15 | Shi Y, Miao J Y, Wang Z Y,et al.Feature selection with l 2,1 - 2 regularization[J].IEEE Transactions on Neural Networks and Learning Systems,2018,29(10):4967-4982. |
| 16 | Bottmer L, Croux C, Wilms I.Sparse regression for large data sets with outliers[J].European Journal of Operational Research,2022,297(2):782-794. |
| 17 | Yuille A L, Rangarajan A.The concave‑convex procedure[J].Neural Computation,2003,15(4):915-936. |
| 18 | Sriperumbudur B, Lanckriet G.On the convergence of the concave-convex procedure[C]// Proceedings of the 22nd International Conference on Neural Information Processing Systems.Vancouver,2009:1759-1767. |
| 19 | Boyd S, Parikh N, Chu E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations and Trends® in Machine Learning,2011,3(1):1-122. |
| [1] | 沙晓鹏, 曹加奇, 李文静, 秦晔. 单目视频图像序列三维重建方法[J]. 东北大学学报(自然科学版), 2024, 45(12): 1680-1687. |
| [2] | 陈龙, 刘巧斌, 陶磊. 基于GS-EKF滤波方法的车辆状态参数估计[J]. 东北大学学报(自然科学版), 2023, 44(8): 1144-1151. |
| [3] | 柳军, 郝丽玲, 何光宇, 徐礼胜. 一种左心室压力个性化估计模型参数子集选择方法[J]. 东北大学学报(自然科学版), 2022, 43(8): 1080-1088. |
| [4] | 佘黎煌, 刘平凡, 张石, 许方晗. 一种高精度低复杂度的改进Root-MUSIC算法[J]. 东北大学学报(自然科学版), 2022, 43(4): 457-463. |
| [5] | 张雪峰, 靳凯净. 基于LMI的离散广义系统的容许性和鲁棒镇定性[J]. 东北大学学报(自然科学版), 2021, 42(4): 463-469. |
| [6] | 张娜, 王璐, 程军娜, 田济荣. 基于分布式压缩感知的自适应距离选通三维成像[J]. 东北大学学报(自然科学版), 2021, 42(4): 516-523. |
| [7] | 叶宁, 宋锦春, 高曦莹, 于忠亮. 基于输出反馈的电液作动器自适应指令滤波控制[J]. 东北大学学报:自然科学版, 2020, 41(9): 1310-1315. |
| [8] | 蔡衍, 周捷, 陈杰, 宋锦春. 电静液执行器双向远程控制的位置跟踪精度研究[J]. 东北大学学报:自然科学版, 2020, 41(5): 710-715. |
| [9] | 赵海, 周冰玲, 朱宏博, 窦圣昶. 基于连续最大流的三维肺实质快速分割算法[J]. 东北大学学报:自然科学版, 2020, 41(4): 470-474. |
| [10] | 康程铭, 赵春雨, 付立新. 基于物理建模法的加工中心主轴热误差建模[J]. 东北大学学报:自然科学版, 2020, 41(4): 528-533. |
| [11] | 郑艳, 高爽. 基于自适应门限的分形维数语音端点检测[J]. 东北大学学报:自然科学版, 2020, 41(1): 7-11. |
| [12] | 冯宝, 张绍荣. 组稀疏贝叶斯逻辑回归的P300信号通道自动选择算法[J]. 东北大学学报:自然科学版, 2019, 40(9): 1245-1251. |
| [13] | 李武杰, 陈从根, 郭立新. 基于微分几何法的主动悬架鲁棒H○∞控制[J]. 东北大学学报:自然科学版, 2019, 40(5): 716-721. |
| [14] | 石春鹤, 吴成东. 基于加权稀疏非负矩阵分解的车脸识别算法[J]. 东北大学学报:自然科学版, 2019, 40(10): 1376-1381. |
| [15] | 王大志, 高明, 李召. 移相全桥的重积分间接滑模控制策略[J]. 东北大学学报:自然科学版, 2018, 39(8): 1069-1074. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||