
东北大学学报(自然科学版) ›› 2025, Vol. 46 ›› Issue (4): 134-143.DOI: 10.12068/j.issn.1005-3026.2025.20239048
• 资源与土木工程 • 上一篇
刘慧娟, 张玄一, 赵衍刚, 卢朝辉
收稿日期:2023-09-14
出版日期:2025-04-15
发布日期:2025-07-01
作者简介:刘慧娟(1995—),女,河南焦作人,北京工业大学博士研究生基金资助:Hui-juan LIU, Xuan-yi ZHANG, Yan-gang ZHAO, Zhao-hui LU
Received:2023-09-14
Online:2025-04-15
Published:2025-07-01
摘要:
为了评估交错桁架钢框架(steel staggered truss framing,SSTF)结构体系的抗震可靠性,以结构底部总水平地震作用达到极限基底剪力作为承载能力极限状态,建立了SSTF结构极限状态函数.以用钢量相同为基准,建立了普通钢框架和6种不同桁架布置形式的SSTF结构分析模型.采用高阶矩法计算了不同地震烈度下普通钢框架和SSTF结构模型的失效概率,绘制了相应的失效概率曲线.结果表明:当地震烈度为6度、7度、8度、9度时,SSTF结构分别开始出现轻微破坏、中等破坏、严重破坏、完全破坏的失效风险;单纯采用竖腹杆不足以提高桁架结构的抗震性能,而增加斜腹杆可以显著降低失效概率;竖腹杆与弦杆之间刚接形式的抗震性能优于铰接形式,刚接形式的失效概率较铰接形式有至少10%比例的降低.
中图分类号:
刘慧娟, 张玄一, 赵衍刚, 卢朝辉. 交错桁架钢框架结构抗震可靠性分析[J]. 东北大学学报(自然科学版), 2025, 46(4): 134-143.
Hui-juan LIU, Xuan-yi ZHANG, Yan-gang ZHAO, Zhao-hui LU. Seismic Reliability Analysis of Steel Staggered Truss Framing Structure[J]. Journal of Northeastern University(Natural Science), 2025, 46(4): 134-143.
| 破坏等级 | VS |
|---|---|
| 基本完好 | VS<VS1 |
| 轻微破坏 | VS1≤VS<VS2 |
| 中等破坏 | VS2≤VS<VS3 |
| 严重破坏 | VS3≤VS<VS4 |
| 完全破坏 | VS≥VS4 |
表1 地震破坏等级与VSi (i=1,…,4)的关系 (levels andVSi (i=1,…,4))
Table 1 Relationship between seismic damage
| 破坏等级 | VS |
|---|---|
| 基本完好 | VS<VS1 |
| 轻微破坏 | VS1≤VS<VS2 |
| 中等破坏 | VS2≤VS<VS3 |
| 严重破坏 | VS3≤VS<VS4 |
| 完全破坏 | VS≥VS4 |
| 第k点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 估计点uk | -3.750 439 7 | -2.366 759 4 | -1.154 454 | 0 | 1.154 454 | 2.366 759 4 | 3.750 439 7 |
| 权重ωk | 5.482 69×10-4 | 3.075 71×10-2 | 0.240 123 3 | 0.457 142 7 | 0.240 123 3 | 3.075 71×10-2 | 5.482 69×10-4 |
表2 估计点uk 和相应权重ωk
Table 2 Estimated points uk and corresponding weights ωk
| 第k点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 估计点uk | -3.750 439 7 | -2.366 759 4 | -1.154 454 | 0 | 1.154 454 | 2.366 759 4 | 3.750 439 7 |
| 权重ωk | 5.482 69×10-4 | 3.075 71×10-2 | 0.240 123 3 | 0.457 142 7 | 0.240 123 3 | 3.075 71×10-2 | 5.482 69×10-4 |
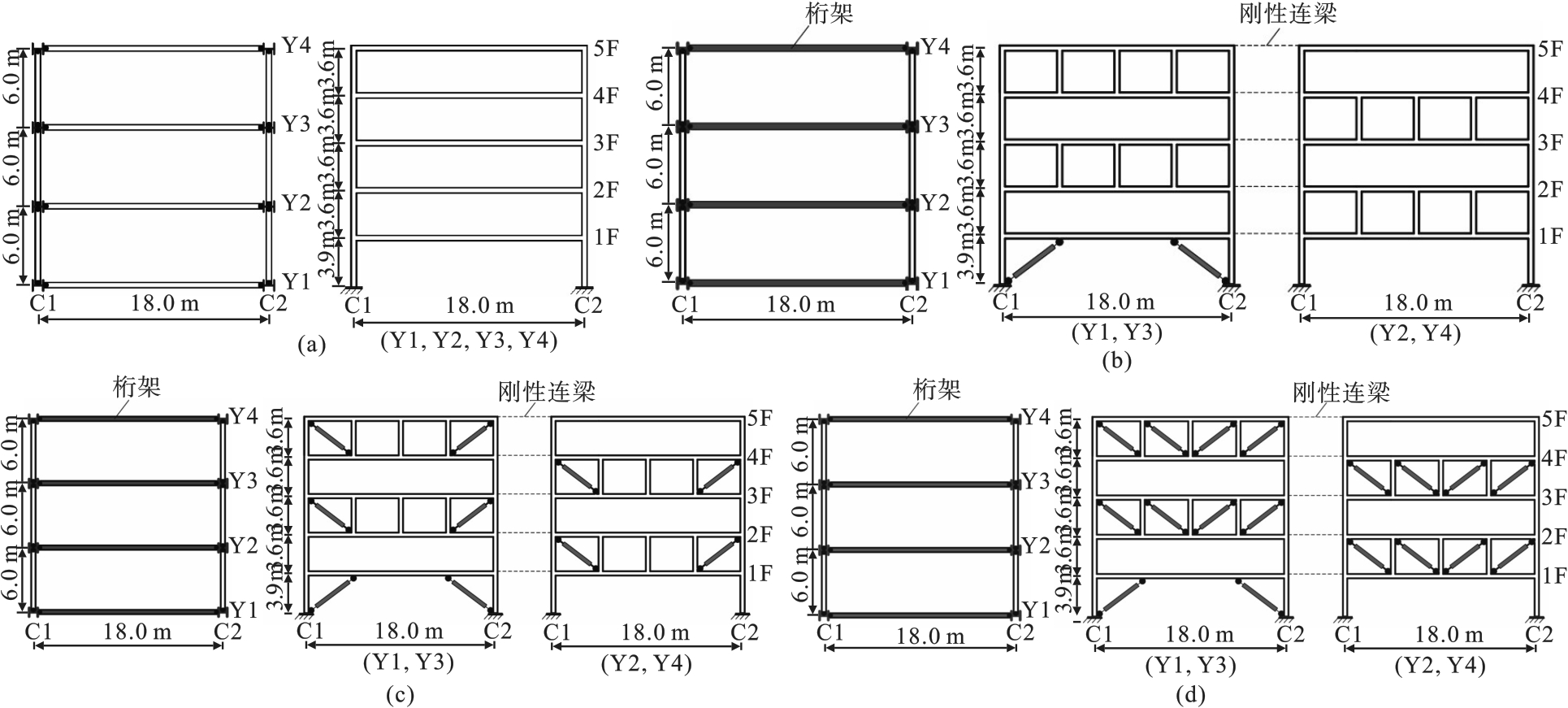
图1 结构模型的平面图及立面图(a)—模型M; (b)—模型RT1,HT1; (c)—模型RT2,HT2; (d)—模型RT3,HT3.
Fig. 1 Plans and elevations of the structural modelαi=∑[MB-CMP(i+1)+MT-CMP(i)]∑[ML-BMP(i)+MR-BMP(i)]. (24)
| 模型 | 层 | αi | 外柱 (Q355) | 弦杆 (Q355) | 竖腹杆 (Q235) | 斜腹杆 (Q235) |
|---|---|---|---|---|---|---|
| M | 5 | 1.1 | H-492×465×15×20 | H-656×301×12×20 | — | — |
| 4 | 2.2 | H-492×465×15×20 | H-656×301×12×20 | — | — | |
| 3 | 2.2 | H-492×465×15×20 | H-656×301×12×20 | — | — | |
| 2 | 2.1 | H-502×465×15×25 | H-656×301×12×20 | — | — | |
| 1 | 2.3 | H-502×465×15×25 | H-656×301×12×20 | — | — | |
RT1 HT1 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-150×150×7×10 | — | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 | |
RT2 HT2 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 | |
RT3 HT3 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 |
表3 结构模型构件横截面尺寸
Table 3 Cross-sectional dimensions of members in structural model
| 模型 | 层 | αi | 外柱 (Q355) | 弦杆 (Q355) | 竖腹杆 (Q235) | 斜腹杆 (Q235) |
|---|---|---|---|---|---|---|
| M | 5 | 1.1 | H-492×465×15×20 | H-656×301×12×20 | — | — |
| 4 | 2.2 | H-492×465×15×20 | H-656×301×12×20 | — | — | |
| 3 | 2.2 | H-492×465×15×20 | H-656×301×12×20 | — | — | |
| 2 | 2.1 | H-502×465×15×25 | H-656×301×12×20 | — | — | |
| 1 | 2.3 | H-502×465×15×25 | H-656×301×12×20 | — | — | |
RT1 HT1 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-150×150×7×10 | — | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-150×150×7×10 | — | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 | |
RT2 HT2 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-125×125×6.5×9 | H-100×100×6×8 | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 | |
RT3 HT3 | 5 | 1.1 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 |
| 4 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 3 | 2.2 | H-400×408×21×21 | H-494×302×13×21 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 2 | 2.1 | H-414×405×18×28 | H-588×300×12×20 | H-125×125×6.5×9 | H-50×50×6×8 | |
| 1 | 2.3 | H-414×405×18×28 | H-588×300×12×20 | — | H-200×200×8×12 |
| 随机变量 | 分布类型 | 均值μG | 变异系数VG |
|---|---|---|---|
| 弹性模量E /MPa | 对数正态 | 2.05×105 | 0.06 |
| 柱、弦杆屈服强度fy1 /MPa | 对数正态 | 355 | 0.08 |
| 竖、斜腹杆屈服强度fy2 /MPa | 对数正态 | 235 | 0.08 |
| 第二刚度系数α | 正态分布 | 0.01 | 0.01 |
| 恒荷载D /(kN·m-2) | 正态分布 | 6 | 0.1 |
| 活荷载L /(kN·m-2) | Gamma | 2 | 0.45 |
表4 随机变量统计信息
Table 4 Statistical information of random variables
| 随机变量 | 分布类型 | 均值μG | 变异系数VG |
|---|---|---|---|
| 弹性模量E /MPa | 对数正态 | 2.05×105 | 0.06 |
| 柱、弦杆屈服强度fy1 /MPa | 对数正态 | 355 | 0.08 |
| 竖、斜腹杆屈服强度fy2 /MPa | 对数正态 | 235 | 0.08 |
| 第二刚度系数α | 正态分布 | 0.01 | 0.01 |
| 恒荷载D /(kN·m-2) | 正态分布 | 6 | 0.1 |
| 活荷载L /(kN·m-2) | Gamma | 2 | 0.45 |
| 点号 | 弹性模量E /MPa | 柱、弦杆屈服强度fy1 /MPa | 竖、斜腹杆屈服强度fy2 /MPa | 第二刚度系数α |
|---|---|---|---|---|
| 1 | 163 431 | 262.3 | 173.6 | 0.009 6 |
| 2 | 177 565 | 292.9 | 193.9 | 0.009 8 |
| 3 | 190 950 | 322.7 | 213.6 | 0.009 9 |
| 4 | 204 632 | 353.9 | 234.3 | 0.010 0 |
| 5 | 219 294 | 388.1 | 256.9 | 0.010 1 |
| 6 | 235 825 | 427.5 | 283.0 | 0.010 2 |
| 7 | 256 220 | 477.5 | 316.1 | 0.010 4 |
表5 随机变量原始空间估计点取值
Table 5 Estimation points in the original space of random variables
| 点号 | 弹性模量E /MPa | 柱、弦杆屈服强度fy1 /MPa | 竖、斜腹杆屈服强度fy2 /MPa | 第二刚度系数α |
|---|---|---|---|---|
| 1 | 163 431 | 262.3 | 173.6 | 0.009 6 |
| 2 | 177 565 | 292.9 | 193.9 | 0.009 8 |
| 3 | 190 950 | 322.7 | 213.6 | 0.009 9 |
| 4 | 204 632 | 353.9 | 234.3 | 0.010 0 |
| 5 | 219 294 | 388.1 | 256.9 | 0.010 1 |
| 6 | 235 825 | 427.5 | 283.0 | 0.010 2 |
| 7 | 256 220 | 477.5 | 316.1 | 0.010 4 |
| 模型 | 性能 水准 | 均值 μG/kN | 标准差 σG | 偏度 α3G | 峰度α4G | 模型 | 性能 水准 | 均值 μG/kN | 标准差 σG | 偏度 α3G | 峰度α4G |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M | VS1 | 1 035.33 | 60.04 | 0.158 | 3.04 | ||||||
| VS2 | 2 589.13 | 150.13 | 0.158 | 3.04 | |||||||
| VS3 | 4 938.27 | 254.59 | -0.512 | 2.72 | |||||||
| VS4 | 5 549.15 | 417.01 | 0.217 | 3.06 | |||||||
| RT1 | VS1 | 821.61 | 48.47 | 0.147 | 3.01 | HT1 | VS1 | 705.72 | 42.08 | 0.165 | 3.05 |
| VS2 | 1 991.79 | 111.27 | 0.155 | 3.06 | VS2 | 1 764.54 | 105.33 | 0.163 | 3.05 | ||
| VS3 | 3 362.88 | 213.44 | -0.106 | 2.86 | VS3 | 3 099.20 | 209.68 | -0.148 | 2.87 | ||
| VS4 | 4 704.49 | 331.14 | -0.155 | 2.78 | VS4 | 4 478.58 | 316.46 | -0.240 | 2.91 | ||
| RT2 | VS1 | 1 235.63 | 82.29 | 0.116 | 3.04 | HT2 | VS1 | 1 175.91 | 82.91 | 0.049 | 3.03 |
| VS2 | 2 860.85 | 167.16 | 0.139 | 3.04 | VS2 | 2 724.35 | 173.28 | -0.080 | 3.34 | ||
| VS3 | 4 940.03 | 234.59 | -0.192 | 3.07 | VS3 | 4 757.30 | 251.41 | -0.626 | 4.03 | ||
| VS4 | 6 027.86 | 381.91 | 0.005 | 3.07 | VS4 | 5 846.05 | 418.16 | -0.393 | 3.84 | ||
| RT3 | VS1 | 1 851.89 | 113.36 | 0.082 | 2.90 | HT3 | VS1 | 1 802.09 | 113.58 | 0.162 | 3.03 |
| VS2 | 3 484.51 | 177.25 | 0.090 | 2.95 | VS2 | 3 379.18 | 171.40 | 0.105 | 2.95 | ||
| VS3 | 5 216.59 | 254.73 | -0.069 | 3.11 | VS3 | 5 074.39 | 246.74 | -0.026 | 3.05 | ||
| VS4 | 6 247.92 | 376.94 | 0.186 | 3.07 | VS4 | 6 099.17 | 373.14 | 0.190 | 3.07 |
表6 各结构模型VSi (i=1,…,4)的前四阶中心矩
Table 6 First four central moments of VSi (i=1,…,4) for different structural models
| 模型 | 性能 水准 | 均值 μG/kN | 标准差 σG | 偏度 α3G | 峰度α4G | 模型 | 性能 水准 | 均值 μG/kN | 标准差 σG | 偏度 α3G | 峰度α4G |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M | VS1 | 1 035.33 | 60.04 | 0.158 | 3.04 | ||||||
| VS2 | 2 589.13 | 150.13 | 0.158 | 3.04 | |||||||
| VS3 | 4 938.27 | 254.59 | -0.512 | 2.72 | |||||||
| VS4 | 5 549.15 | 417.01 | 0.217 | 3.06 | |||||||
| RT1 | VS1 | 821.61 | 48.47 | 0.147 | 3.01 | HT1 | VS1 | 705.72 | 42.08 | 0.165 | 3.05 |
| VS2 | 1 991.79 | 111.27 | 0.155 | 3.06 | VS2 | 1 764.54 | 105.33 | 0.163 | 3.05 | ||
| VS3 | 3 362.88 | 213.44 | -0.106 | 2.86 | VS3 | 3 099.20 | 209.68 | -0.148 | 2.87 | ||
| VS4 | 4 704.49 | 331.14 | -0.155 | 2.78 | VS4 | 4 478.58 | 316.46 | -0.240 | 2.91 | ||
| RT2 | VS1 | 1 235.63 | 82.29 | 0.116 | 3.04 | HT2 | VS1 | 1 175.91 | 82.91 | 0.049 | 3.03 |
| VS2 | 2 860.85 | 167.16 | 0.139 | 3.04 | VS2 | 2 724.35 | 173.28 | -0.080 | 3.34 | ||
| VS3 | 4 940.03 | 234.59 | -0.192 | 3.07 | VS3 | 4 757.30 | 251.41 | -0.626 | 4.03 | ||
| VS4 | 6 027.86 | 381.91 | 0.005 | 3.07 | VS4 | 5 846.05 | 418.16 | -0.393 | 3.84 | ||
| RT3 | VS1 | 1 851.89 | 113.36 | 0.082 | 2.90 | HT3 | VS1 | 1 802.09 | 113.58 | 0.162 | 3.03 |
| VS2 | 3 484.51 | 177.25 | 0.090 | 2.95 | VS2 | 3 379.18 | 171.40 | 0.105 | 2.95 | ||
| VS3 | 5 216.59 | 254.73 | -0.069 | 3.11 | VS3 | 5 074.39 | 246.74 | -0.026 | 3.05 | ||
| VS4 | 6 247.92 | 376.94 | 0.186 | 3.07 | VS4 | 6 099.17 | 373.14 | 0.190 | 3.07 |
| 样本序号 | E | fy1 | fy2 | α | VS1 | VS2 | VS3 | VS4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 163 430 | 355 | 235 | 0.01 | 1 061.8 | 2 339.5 | 4 281.9 | 5 705.2 |
| 2 | 177 570 | 355 | 235 | 0.01 | 1 138.6 | 2 522.9 | 4 565.6 | 5 824.3 |
| 3 | 190 950 | 355 | 235 | 0.01 | 1 211.1 | 2 694.7 | 4 745.8 | 5 937.6 |
| 4 | 204 630 | 355 | 235 | 0.01 | 1 284.7 | 2 870.0 | 4 987.3 | 6 048.2 |
| 5 | 219 290 | 355 | 235 | 0.01 | 1 363.0 | 3 054.8 | 5 197.5 | 6 155.0 |
| 6 | 235 830 | 355 | 235 | 0.01 | 1 450.9 | 3 262.9 | 5 397.2 | 6 245.2 |
| 7 | 256 220 | 355 | 235 | 0.01 | 1 558.9 | 3 516.4 | 5 578.7 | 6 354.9 |
| 8 | 205 000 | 262.3 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 235.0 | 4 714.6 |
| 9 | 205 000 | 292.9 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 583.5 | 5 181.7 |
| 10 | 205 000 | 322.7 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 841.1 | 5 619.2 |
| 11 | 205 000 | 353.9 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 991.7 | 6 037.4 |
| 12 | 205 000 | 388.1 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 053.9 | 6 442.1 |
| 13 | 205 000 | 427.5 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 071.0 | 6 898.8 |
| 14 | 205 000 | 477.5 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 071.0 | 7 478.9 |
| 15 | 205 000 | 355 | 173.6 | 0.01 | 1 110.0 | 2 673.7 | 4 618.4 | 5 741.6 |
| 16 | 205 000 | 355 | 193.9 | 0.01 | 1 139.9 | 2 712.3 | 4 748.0 | 5 841.2 |
| 17 | 205 000 | 355 | 213.6 | 0.01 | 1 207.7 | 2 788.0 | 4 868.9 | 5 941.0 |
| 18 | 205 000 | 355 | 234.3 | 0.01 | 1 284.0 | 2 871.6 | 4 989.4 | 6 046.8 |
| 19 | 205 000 | 355 | 256.9 | 0.01 | 1 367.4 | 2 960.9 | 5 110.1 | 6 156.1 |
| 20 | 205 000 | 355 | 283 | 0.01 | 1 354.7 | 3 064.3 | 5 259.2 | 6 273.9 |
| 21 | 205 000 | 355 | 316.1 | 0.01 | 1 544.2 | 3 093.9 | 5 439.0 | 6 407.2 |
| 22 | 205 000 | 355 | 235 | 0.009 6 | 1 286.3 | 2 873.8 | 4 991.3 | 6 042.5 |
| 23 | 205 000 | 355 | 235 | 0.009 8 | 1 286.5 | 2 874.3 | 4 992.5 | 6 046.6 |
| 24 | 205 000 | 355 | 235 | 0.009 9 | 1 286.6 | 2 874.5 | 4 993.1 | 6 048.6 |
| 25 | 205 000 | 355 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 993.7 | 6 050.6 |
| 26 | 205 000 | 355 | 235 | 0.010 1 | 1 286.7 | 2 875.0 | 4 994.3 | 6 052.7 |
| 27 | 205 000 | 355 | 235 | 0.010 2 | 1 286.8 | 2 875.2 | 4 995.0 | 6 054.7 |
| 28 | 205 000 | 355 | 235 | 0.010 4 | 1 286.9 | 2 875.7 | 4 996.2 | 6 058.8 |
表7 RT2模型的样本点及对应的VSi (i=1,…,4)
Table 7 VSi (i=1,…,4) and different sample points of RT2 model
| 样本序号 | E | fy1 | fy2 | α | VS1 | VS2 | VS3 | VS4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 163 430 | 355 | 235 | 0.01 | 1 061.8 | 2 339.5 | 4 281.9 | 5 705.2 |
| 2 | 177 570 | 355 | 235 | 0.01 | 1 138.6 | 2 522.9 | 4 565.6 | 5 824.3 |
| 3 | 190 950 | 355 | 235 | 0.01 | 1 211.1 | 2 694.7 | 4 745.8 | 5 937.6 |
| 4 | 204 630 | 355 | 235 | 0.01 | 1 284.7 | 2 870.0 | 4 987.3 | 6 048.2 |
| 5 | 219 290 | 355 | 235 | 0.01 | 1 363.0 | 3 054.8 | 5 197.5 | 6 155.0 |
| 6 | 235 830 | 355 | 235 | 0.01 | 1 450.9 | 3 262.9 | 5 397.2 | 6 245.2 |
| 7 | 256 220 | 355 | 235 | 0.01 | 1 558.9 | 3 516.4 | 5 578.7 | 6 354.9 |
| 8 | 205 000 | 262.3 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 235.0 | 4 714.6 |
| 9 | 205 000 | 292.9 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 583.5 | 5 181.7 |
| 10 | 205 000 | 322.7 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 841.1 | 5 619.2 |
| 11 | 205 000 | 353.9 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 991.7 | 6 037.4 |
| 12 | 205 000 | 388.1 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 053.9 | 6 442.1 |
| 13 | 205 000 | 427.5 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 071.0 | 6 898.8 |
| 14 | 205 000 | 477.5 | 235 | 0.01 | 1 286.6 | 2 874.7 | 5 071.0 | 7 478.9 |
| 15 | 205 000 | 355 | 173.6 | 0.01 | 1 110.0 | 2 673.7 | 4 618.4 | 5 741.6 |
| 16 | 205 000 | 355 | 193.9 | 0.01 | 1 139.9 | 2 712.3 | 4 748.0 | 5 841.2 |
| 17 | 205 000 | 355 | 213.6 | 0.01 | 1 207.7 | 2 788.0 | 4 868.9 | 5 941.0 |
| 18 | 205 000 | 355 | 234.3 | 0.01 | 1 284.0 | 2 871.6 | 4 989.4 | 6 046.8 |
| 19 | 205 000 | 355 | 256.9 | 0.01 | 1 367.4 | 2 960.9 | 5 110.1 | 6 156.1 |
| 20 | 205 000 | 355 | 283 | 0.01 | 1 354.7 | 3 064.3 | 5 259.2 | 6 273.9 |
| 21 | 205 000 | 355 | 316.1 | 0.01 | 1 544.2 | 3 093.9 | 5 439.0 | 6 407.2 |
| 22 | 205 000 | 355 | 235 | 0.009 6 | 1 286.3 | 2 873.8 | 4 991.3 | 6 042.5 |
| 23 | 205 000 | 355 | 235 | 0.009 8 | 1 286.5 | 2 874.3 | 4 992.5 | 6 046.6 |
| 24 | 205 000 | 355 | 235 | 0.009 9 | 1 286.6 | 2 874.5 | 4 993.1 | 6 048.6 |
| 25 | 205 000 | 355 | 235 | 0.01 | 1 286.6 | 2 874.7 | 4 993.7 | 6 050.6 |
| 26 | 205 000 | 355 | 235 | 0.010 1 | 1 286.7 | 2 875.0 | 4 994.3 | 6 052.7 |
| 27 | 205 000 | 355 | 235 | 0.010 2 | 1 286.8 | 2 875.2 | 4 995.0 | 6 054.7 |
| 28 | 205 000 | 355 | 235 | 0.010 4 | 1 286.9 | 2 875.7 | 4 996.2 | 6 058.8 |
| 模型 | 性能 水准 | 失效概率 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| I=5 | I=6 | I=7 | I=8 | I=9 | I=10 | I=11 | I=12 | ||
| M | VS1 | 1.470×10-32 | 1.537×10-7 | 0.779 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 6.360×10-17 | 1.099×10-46 | 4.827×10-13 | 0.14 | 0.999 | 1 | 1 | 1 | |
| VS3 | 6.474×10-6 | 1.741×10-6 | 4.835×10-9 | 2.053×10-13 | 0.241 | 1 | 1 | 1 | |
| VS4 | 5.760×10-64 | 2.790×10-11 | 6.785×10-89 | 1.110×10-13 | 6.255×10-2 | 1 | 1 | 1 | |
| RT1 | VS1 | 1.200×10-22 | 9.838×10-4 | 0.994 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 1.788×10-59 | 8.125×10-29 | 7.440×10-7 | 0.862 | 1 | 1 | 1 | 1 | |
| VS3 | 1.848×10-16 | 1.737×10-18 | 1.499×10-30 | 7.886×10-4 | 0.991 | 1 | 1 | 1 | |
| VS4 | 7.981×10-11 | 2.432×10-11 | 1.216×10-13 | 1.538×10-9 | 0.396 | 1 | 1 | 1 | |
| RT2 | VS1 | 1.945×10-29 | 1.849×10-10 | 0.255 | 0.999 | 1 | 1 | 1 | 1 |
| VS2 | 3.521×10-83 | 5.932×10-48 | 7.302×10-16 | 2.751×10-2 | 0.999 | 1 | 1 | 1 | |
| VS3 | 2.876×10-38 | 8.245×10-35 | 9.882×10-27 | 2.894×10-11 | 0.237 | 1 | 1 | 1 | |
| VS4 | 1.089×10-29 | 8.417×10-28 | 1.544×10-23 | 1.254×10-13 | 1.110×10-2 | 1 | 1 | 1 | |
| RT3 | VS1 | 2.375×10-16 | 6.333×10-29 | 2.151×10-5 | 0.949 | 1 | 1 | 1 | 1 |
| VS2 | 7.315×10-25 | 3.877×10-32 | 3.499×10-31 | 9.865×10-5 | 0.984 | 1 | 1 | 1 | |
| VS3 | 2.128×10-31 | 1.436×10-29 | 6.211×10-25 | 2.185×10-12 | 0.118 | 1 | 1 | 1 | |
| VS4 | 1.134×10-93 | 1.310×10-80 | 1.602×10-51 | 9.109×10-19 | 4.028×10-3 | 1 | 1 | 1 | |
| HT1 | VS1 | 1.526×10-15 | 3.614×10-2 | 0.999 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 1.058×10-61 | 1.106×10-23 | 1.104×10-4 | 0.977 | 1 | 1 | 1 | 1 | |
| VS3 | 4.110×10-18 | 1.823×10-20 | 1.931×10-18 | 7.411×10-3 | 0.998 | 1 | 1 | 1 | |
| VS4 | 3.716×10-19 | 2.532×10-20 | 1.584×10-25 | 2.056×10-7 | 0.547 | 1 | 1 | 1 | |
| HT2 | VS1 | 2.799×10-22 | 1.115×10-8 | 0.398 | 0.999 | 1 | 1 | 1 | 1 |
| VS2 | 2.074×10-15 | 8.337×10-14 | 2.027×10-9 | 7.173×10-2 | 0.999 | 1 | 1 | 1 | |
| VS3 | 5.247×10-13 | 2.287×10-12 | 4.390×10-11 | 1.999×10-7 | 0.349 | 1 | 1 | 1 | |
| VS4 | 1.900×10-10 | 5.091×10-10 | 3.692×10-9 | 3.893×10-7 | 2.810×10-2 | 1 | 1 | 1 | |
| HT3 | VS1 | 1.450×10-41 | 1.335×10-25 | 6.731×10-5 | 0.966 | 1 | 1 | 1 | 1 |
| VS2 | 6.292×10-23 | 2.226×10-30 | 2.852×10-29 | 2.753×10-4 | 0.991 | 1 | 1 | 1 | |
| VS3 | 5.214×10-43 | 1.422×10-39 | 1.924×10-30 | 2.425×10-12 | 0.172 | 1 | 1 | 1 | |
| VS4 | 1.384×10-98 | 1.961×10-83 | 3.893×10-51 | 7.177×10-18 | 7.419×10-3 | 1 | 1 | 1 | |
表8 不同地震烈度下各结构模型4种极限状态下的失效概率
Table 8 Failure probabilities of each structural model at four limit states under different seismic intensities
| 模型 | 性能 水准 | 失效概率 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| I=5 | I=6 | I=7 | I=8 | I=9 | I=10 | I=11 | I=12 | ||
| M | VS1 | 1.470×10-32 | 1.537×10-7 | 0.779 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 6.360×10-17 | 1.099×10-46 | 4.827×10-13 | 0.14 | 0.999 | 1 | 1 | 1 | |
| VS3 | 6.474×10-6 | 1.741×10-6 | 4.835×10-9 | 2.053×10-13 | 0.241 | 1 | 1 | 1 | |
| VS4 | 5.760×10-64 | 2.790×10-11 | 6.785×10-89 | 1.110×10-13 | 6.255×10-2 | 1 | 1 | 1 | |
| RT1 | VS1 | 1.200×10-22 | 9.838×10-4 | 0.994 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 1.788×10-59 | 8.125×10-29 | 7.440×10-7 | 0.862 | 1 | 1 | 1 | 1 | |
| VS3 | 1.848×10-16 | 1.737×10-18 | 1.499×10-30 | 7.886×10-4 | 0.991 | 1 | 1 | 1 | |
| VS4 | 7.981×10-11 | 2.432×10-11 | 1.216×10-13 | 1.538×10-9 | 0.396 | 1 | 1 | 1 | |
| RT2 | VS1 | 1.945×10-29 | 1.849×10-10 | 0.255 | 0.999 | 1 | 1 | 1 | 1 |
| VS2 | 3.521×10-83 | 5.932×10-48 | 7.302×10-16 | 2.751×10-2 | 0.999 | 1 | 1 | 1 | |
| VS3 | 2.876×10-38 | 8.245×10-35 | 9.882×10-27 | 2.894×10-11 | 0.237 | 1 | 1 | 1 | |
| VS4 | 1.089×10-29 | 8.417×10-28 | 1.544×10-23 | 1.254×10-13 | 1.110×10-2 | 1 | 1 | 1 | |
| RT3 | VS1 | 2.375×10-16 | 6.333×10-29 | 2.151×10-5 | 0.949 | 1 | 1 | 1 | 1 |
| VS2 | 7.315×10-25 | 3.877×10-32 | 3.499×10-31 | 9.865×10-5 | 0.984 | 1 | 1 | 1 | |
| VS3 | 2.128×10-31 | 1.436×10-29 | 6.211×10-25 | 2.185×10-12 | 0.118 | 1 | 1 | 1 | |
| VS4 | 1.134×10-93 | 1.310×10-80 | 1.602×10-51 | 9.109×10-19 | 4.028×10-3 | 1 | 1 | 1 | |
| HT1 | VS1 | 1.526×10-15 | 3.614×10-2 | 0.999 | 1 | 1 | 1 | 1 | 1 |
| VS2 | 1.058×10-61 | 1.106×10-23 | 1.104×10-4 | 0.977 | 1 | 1 | 1 | 1 | |
| VS3 | 4.110×10-18 | 1.823×10-20 | 1.931×10-18 | 7.411×10-3 | 0.998 | 1 | 1 | 1 | |
| VS4 | 3.716×10-19 | 2.532×10-20 | 1.584×10-25 | 2.056×10-7 | 0.547 | 1 | 1 | 1 | |
| HT2 | VS1 | 2.799×10-22 | 1.115×10-8 | 0.398 | 0.999 | 1 | 1 | 1 | 1 |
| VS2 | 2.074×10-15 | 8.337×10-14 | 2.027×10-9 | 7.173×10-2 | 0.999 | 1 | 1 | 1 | |
| VS3 | 5.247×10-13 | 2.287×10-12 | 4.390×10-11 | 1.999×10-7 | 0.349 | 1 | 1 | 1 | |
| VS4 | 1.900×10-10 | 5.091×10-10 | 3.692×10-9 | 3.893×10-7 | 2.810×10-2 | 1 | 1 | 1 | |
| HT3 | VS1 | 1.450×10-41 | 1.335×10-25 | 6.731×10-5 | 0.966 | 1 | 1 | 1 | 1 |
| VS2 | 6.292×10-23 | 2.226×10-30 | 2.852×10-29 | 2.753×10-4 | 0.991 | 1 | 1 | 1 | |
| VS3 | 5.214×10-43 | 1.422×10-39 | 1.924×10-30 | 2.425×10-12 | 0.172 | 1 | 1 | 1 | |
| VS4 | 1.384×10-98 | 1.961×10-83 | 3.893×10-51 | 7.177×10-18 | 7.419×10-3 | 1 | 1 | 1 | |
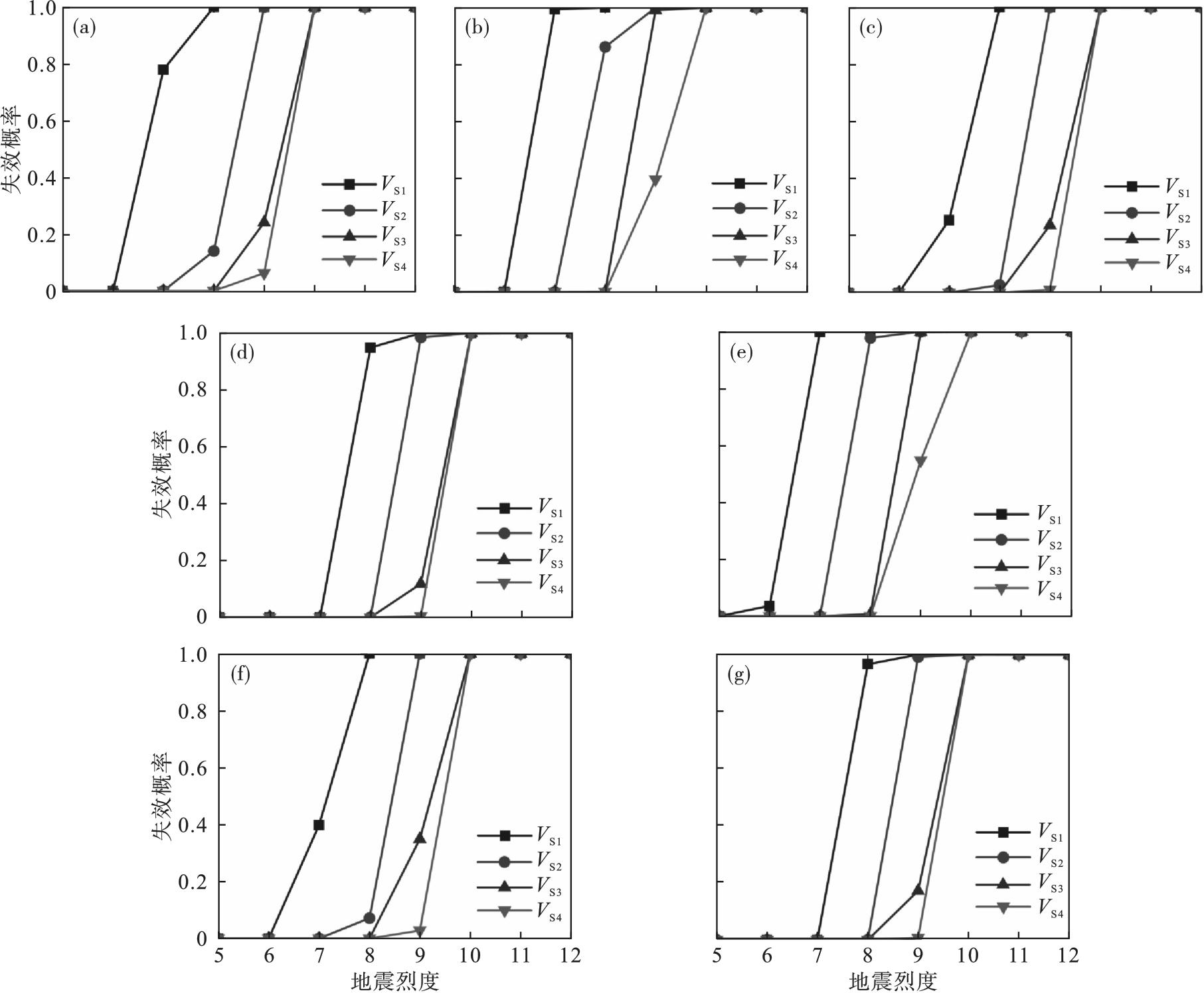
图5 各结构模型不同地震烈度下的失效概率(a)—M模型; (b)—RT1模型; (c)—RT2模型; (d)—RT3模型; (e)—HT1模型; (f)—HT2模型; (g)—HT3模型.
Fig.5 Failure probabilities of different structural models under various seismic intensities
| 1 | Scalzi J B. The staggered truss system-structural considerations[J]. Engineering Journal, 1971, 8(4): 138-143. |
| 2 | 周绪红,莫涛,蔡益燕,等 .新型交错桁架结构体系的应用[J].钢结构, 2000, 15(2): 16-18. |
| Zhou Xu-hong, Mo Tao, Cai Yi-yan, et al. The use of new type staggered truss structure[J]. Steel Construction, 2000, 15(2): 16-18. | |
| 3 | 甘丹,周绪红,周期石 .交错桁架钢框架结构抗震性能研究现状[J].建筑钢结构进展, 2019, 21(4): 1-10. |
| Gan Dan, Zhou Xu-hong, Zhou Qi-shi. A review on the seismic behavior of steel staggered truss framing system[J]. Progress in Steel Building Structures, 2019, 21(4): 1-10. | |
| 4 | 周绪红,莫涛 .交错桁架结构体系的空间二阶弹塑性全过程分析[J].土木工程学报, 2005, 38(5): 10-14. |
| Zhou Xu-hong, Mo Tao. A nonlinear analysis approach for staggered-truss structure systems of three-dimensional elasto-plasticity[J]. China Civil Engineering Journal, 2005, 38(5): 10-14. | |
| 5 | Kim J, Lee J, Kim B. Seismic retrofit schemes for staggered truss structures[J]. Engineering Structures, 2015, 102: 93-107. |
| 6 | Kim J, Kim S. Performance-based seismic design of staggered truss frames with friction dampers[J]. Thin-Walled Structures, 2017, 111: 197-209. |
| 7 | 周绪红,莫涛,刘永健,等 .高层钢结构交错桁架结构的试验研究[J].建筑结构学报, 2006, 27(5): 86-92. |
| Zhou Xu-hong, Mo Tao, Liu Yong-jian, et al. Experimental study on high-rise staggered truss steel structure[J]. Journal of Building Structures, 2006, 27(5): 86-92. | |
| 8 | Hansen R J, Le Messurier W J, Paul P J. New steel framing system promises major saving in high-rise apartment[J]. Architecture Record, 1966, 139(6): 191-196. |
| 9 | Gupta R P, Goel S C. Dynamic analysis of staggered truss framing system[J]. Journal of the Structural Division, 1972, 98(7): 1475-1492. |
| 10 | Ionnides S A, Lindsey S D. Staggered truss adapted to high rise[J]. Civil Engineering, 1985, 6: 44-47. |
| 11 | 潘英,周绪红 .交错桁架体系的抗震性能动力分析[J].土木工程学报, 2002, 35(4): 12-16. |
| Pan Ying, Zhou Xu-hong. Aseismic behavior of the staggered-truss system[J]. China Civil Engineering Journal, 2002, 35(4): 12-16. | |
| 12 | Liu Z, Zhang Z. Artificial neural network based method for seismic fragility analysis of steel frames[J]. KSCE Journal of Civil Engineering, 2018, 22(2): 708-717. |
| 13 | Gur S, Xie Y Z, Desroches R. Seismic fragility analyses of steel building frames installed with superelastic shape memory alloy dampers: comparison with yielding dampers[J]. Journal of Intelligent Material Systems and Structures, 2019, 30(18/19): 2670-2687. |
| 14 | Sun B Y, Zhang Y T, Huang C G. Machine learning-based seismic fragility analysis of large-scale steel buckling restrained brace frames[J]. Computer Modeling in Engineering & Sciences, 2020, 125(2): 755-776. |
| 15 | Hasofer A M, Lind N C. Exact and invariant second-moment code format[J]. Journal of the Engineering Mechanics Division, 1974, 100(1): 111-121. |
| 16 | Der Kiureghian A, De Stefano M. Efficient algorithm for second-order reliability analysis[J]. Journal of Engineering Mechanics, 1991, 117(12): 2904-2923. |
| 17 | Zhao Y G, Lu Z H. Structural reliability: approaches from perspectives of statistical moments[M]. Hoboken: Wiley-Blackwell, 2021. |
| 18 | Ogawa K, Tada M. Combined non-linear analysis for plane frame (“clap”) [C]//Architectural Institute of Japan. Proceedings. of 17th Symposium on Computer Technology on Information Systems and Applications. Tokyo: Showa Intelligence Press, 1994: 79-84. |
| 19 | Omori F. Seismic experiments on the fracturing and overturning of columns[J]. Publications of the Earthquake Investigation Committe in Foreign Language, 1996, 4: 69. |
| 20 | 齐怀恩, 王光远. 公路桥梁抗震设防标准的研究[J]. 东北公路, 1999(4): 48-51. |
| Qi Huai-en, Wang Guang-yuan. Study of aseismatic fortify standard of highway bridge[J]. Northeastern Highway, 1999(4): 48-51. | |
| 21 | Zhao Y G, Lu Z H. Fourth-moment standardization for structural reliability assessment[J]. Journal of Structural Engineering, 2007, 133(7): 916-924. |
| 22 | Zhang X Y, Zhao Y G, Lu Z H. Unified Hermite polynomial model and its application in estimating non-Gaussian processes[J]. Journal of Engineering Mechanics, 2019, 145(3): 04019001. |
| 23 | Zhao Y G, Ono T. New point estimates for probability moments[J]. Journal of Engineering Mechanics, 2000, 126(4): 433-436. |
| 24 | 刘慧娟 .不同桁架形式对多层SSTF结构抗震性能的影响[D].桂林:桂林理工大学,2021. |
| Liu Hui-juan. Influence of different truss forms on seismic performance of multi-story SSTF structure [D]. Guilin: Guilin University of Technology, 2021. | |
| 25 | Bao E H, Chen Y Y, Zou C L, et al. Dynamic performance of low-rise steel frame with exposed steel column base[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2018, 171(12): 979-991. |
| 26 | Kim M T. Analytical study on the effect of P-Δ effect on the response of high-rise steel buildings to long-period earthquake motion[D]. Kyoto: Kyoto University, 2010. |
| 27 | 夏正中. 钢结构可靠度分析[J]. 冶金建筑, 1981, 11(12): 43-46. |
| Xia Zheng-zhong. Reliability analysis of steel structure[J]. Industrial Construction, 1981, 11(12): 43-46. | |
| 28 | 宋鹏彦. 结构整体可靠度方法及RC框架非线性整体抗震可靠度分析[D]. 哈尔滨: 哈尔滨工业大学, 2012. |
| Song Peng-yan. Structural integral reliability method and nonlinear integral seismic reliability analysis of RC frame[D]. Harbin: Harbin Institute of Technology, 2012. | |
| 29 | 吕大刚, 宋鹏彦, 于晓辉, 等. 基于矩法的结构非线性整体抗震可靠性分析[J]. 建筑结构学报, 2010, 31(sup2): 119-124. |
| Da-gang Lyu, Song Peng-yan, Yu Xiao-hui,et al. Nonlinear global seismic reliability analysis of structures based on moment methods[J]. Journal of Building Structures, 2010, 31(sup2): 119-124. | |
| 30 | Hohenbichler M, Rackwitz R. Non-normal dependent vectors in structural safety[J]. Journal of the Engineering Mechanics Division, 1981, 107(6): 1227-1238. |
| [1] | 高海洋, 王连广, 陈百玲. 轴压下FRP管-混凝土-钢管组合柱可靠性分析[J]. 东北大学学报(自然科学版), 2024, 45(3): 430-438. |
| [2] | 曹汝男, 孙志礼, 郭凡逸, 王健. 基于Kriging和Monte Carlo的动态可靠性算法[J]. 东北大学学报(自然科学版), 2021, 42(5): 658-664. |
| [3] | 刘博林, 谢里阳. 一种改进的全局可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(7): 943-948. |
| [4] | 于震梁, 孙志礼, 张毅博, 王健. 一种自适应PC-Kriging模型的结构可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(5): 667-672. |
| [5] | 曹汝男, 孙志礼, 张毅博, 王健. 基于主动学习的复杂机械结构的可靠性分析[J]. 东北大学学报:自然科学版, 2020, 41(2): 223-228. |
| [6] | 张毅博, 孙志礼, 闫玉涛, 王健. 一种基于失效概率相对误差估计的可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(2): 229-234. |
| [7] | 于震梁, 孙志礼, 曹汝男, 张毅博. 基于PC-Kriging模型与主动学习的齿轮热传递误差可靠性分析[J]. 东北大学学报:自然科学版, 2019, 40(12): 1750-1754. |
| [8] | 朱俊樸, 戴公连, 苏海霆, 梁金宝. 基于高阶矩法的梁-轨系统温度作用代表值[J]. 东北大学学报:自然科学版, 2017, 38(8): 1195-1200. |
| [9] | 李艺, 董金霞, TAN Kiang Hwee. 长期荷载作用下SFRC梁承载能力极限状态可靠性分析[J]. 东北大学学报:自然科学版, 2017, 38(7): 1055-1059. |
| [10] | 张耀满, 殷鑫贤, 林秀丽, 由昭鹏. 数控车床的液体动静压轴承油膜压力特性[J]. 东北大学学报:自然科学版, 2017, 38(5): 695-699. |
| [11] | 涂宏茂, 孙志礼, 姬广振, 钱云鹏. 考虑失效模式相关性的机械系统可靠性分析[J]. 东北大学学报:自然科学版, 2017, 38(10): 1453-1458. |
| [12] | 胡成志, 白敏丽, 吕继组, 王鹏. 纳米颗粒影响润滑膜摩擦特性的分子动力学[J]. 东北大学学报:自然科学版, 2015, 36(3): 415-418. |
| [13] | 张文献;刘心亮;罗冰;李明光;. 通过裂缝特征快速评估桥梁承载能力的试验研究[J]. 东北大学学报(自然科学版), 2008, 29(9): 1346-1349. |
| [14] | 苏长青;张义民;. 质量慢变转子系统碰摩的可靠性分析[J]. 东北大学学报(自然科学版), 2008, 29(11): 1605-1608. |
| [15] | 刘均;黄宝宗;. 压剪组合作用下复合材料壁板的后屈曲承载能力[J]. 东北大学学报(自然科学版), 2007, 28(1): 149-152. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||