
东北大学学报(自然科学版) ›› 2024, Vol. 45 ›› Issue (10): 1485-1493.DOI: 10.12068/j.issn.1005-3026.2024.10.015
• 资源与土木工程 • 上一篇
收稿日期:2023-05-24
出版日期:2024-10-31
发布日期:2024-12-31
通讯作者:
何畅
作者简介:丁发兴(1979-),男,浙江瑞安人,中南大学教授,博士生导师.
基金资助:
Fa-xing DING1,2, Shu-dong SHU1, Jing-ke ZHANG1,3, Chang HE1( )
)
Received:2023-05-24
Online:2024-10-31
Published:2024-12-31
Contact:
Chang HE
About author:HE Chang,E-mail:hechang@csu.edu.cn摘要:
为揭示开口截面钢-混凝土组合梁抗扭工作机理,提出适用于工程实际的抗扭承载力计算方法,建立了工字钢-混凝土组合梁精细有限元分析模型,探究了纯扭作用下混凝土板截面尺寸、混凝土强度、钢梁截面尺寸、钢梁强度、配筋率、宽跨比等参数对组合梁抗扭力学性能的影响.基于组合作用和叠加原理,提出了考虑混凝土板和钢梁腹板与翼缘抗扭贡献的开口截面钢-混凝土组合梁抗扭承载力计算公式.结果表明:组合梁抗扭承载力主要由混凝土板承担,混凝土板抗扭承载力组合作用系数为1.1,与实验结果吻合较好,能较好预测组合梁抗扭承载力.
中图分类号:
丁发兴, 束舒东, 张经科, 何畅. 开口截面钢-混凝土组合梁纯扭力学性能[J]. 东北大学学报(自然科学版), 2024, 45(10): 1485-1493.
Fa-xing DING, Shu-dong SHU, Jing-ke ZHANG, Chang HE. Mechanical Performance of Open Cross-Section Steel-Concrete Composite Beams Under Pure Torsion[J]. Journal of Northeastern University(Natural Science), 2024, 45(10): 1485-1493.
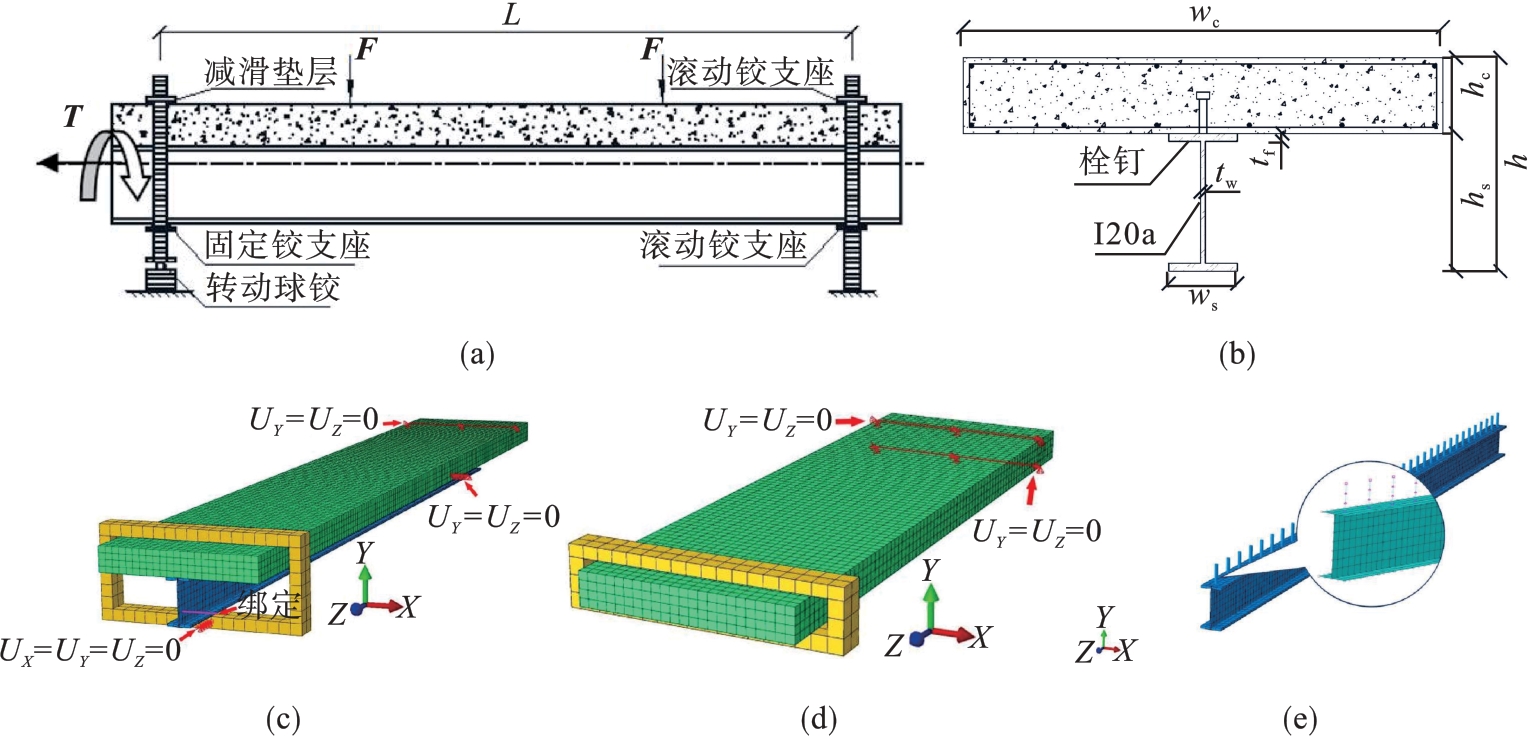
图1 组合梁抗扭计算简图及有限元模型(a)—计算简图; (b)—截面示意图; (c)—整体有限元模型; (d)—混凝土板有限元模型; (e)—钢梁有限元模型.
Fig.1 Calculation diagram and finite element model of torsional resistance of composite beams
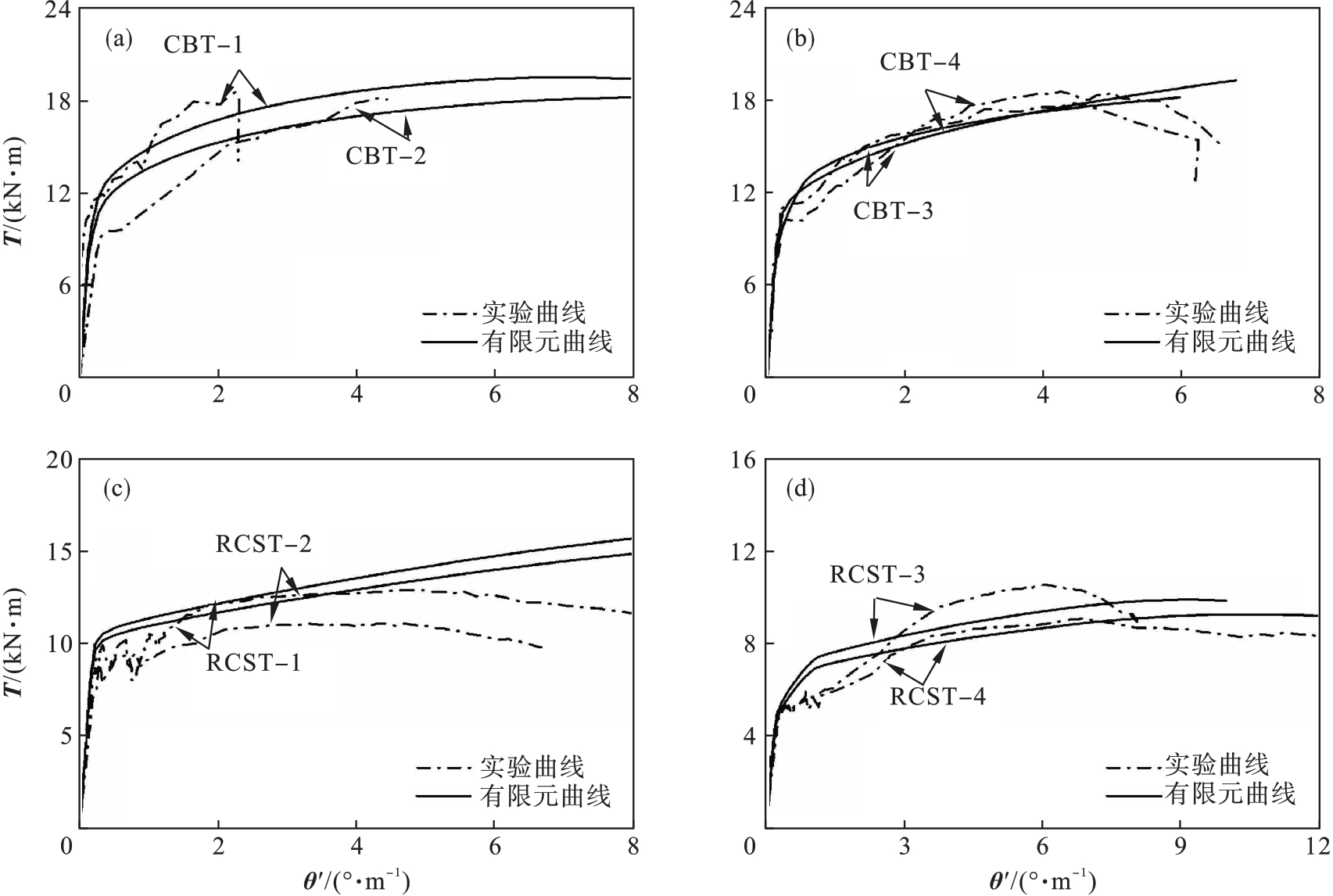
图2 实验与有限元扭矩-扭率曲线对比(a)—钢-混凝土组合梁CBT-1,CBT-2; (b)—钢-混凝土组合梁CBT-3,CBT-4;(c)—钢筋混凝土板RCST-1,RCST-2; (d)—钢筋混凝土板RCST-3,RCST-4.
Fig.2 Comparison diagram of T-θ′ curves between experiment and finite element analysis
| 试件编号 | wc×hc×ws×hs/mm | L/mm | s/mm | σs/MPa | σy/MPa | σcu/MPa | Te/(kN·m) | Ta/(kN·m) | Te/Ta |
|---|---|---|---|---|---|---|---|---|---|
| CBT-1 | 700×110×100×200 | 3 800 | 100 | 299.6 | 302.2 | 41.0 | 18.34 | 19.27 | 0.95 |
| CBT-2 | 700×110×100×200 | 3 800 | 80 | 299.6 | 302.2 | 35.5 | 18.20 | 17.88 | 1.02 |
| CBT-3 | 700×110×100×200 | 1 800 | 180 | 299.6 | 328.1 | 26.0 | 17.78 | 16.50 | 1.08 |
| CBT-4 | 700×110×100×200 | 1 800 | 130 | 299.6 | 328.1 | 32.0 | 18.52 | 19.78 | 0.94 |
| RCST-1 | 700×110×100×200 | 3 800 | 100 | — | 343.0 | 39.5 | 12.94 | 13.80 | 0.94 |
| RCST-2 | 700×110×100×200 | 3 800 | 80 | — | 343.0 | 37.6 | 11.24 | 12.78 | 0.88 |
| RCST-3 | 700×110×100×200 | 1 800 | 180 | — | 343.0 | 40.0 | 10.51 | 9.88 | 1.06 |
| RCST-4 | 700×110×100×200 | 1 800 | 130 | — | 343.0 | 36.6 | 9.07 | 9.24 | 0.98 |
表1 抗扭承载力有限元分析结果与实验结果比较
Table 1 Comparison of finite element analysis and experiment results of torsional bearing capacity
| 试件编号 | wc×hc×ws×hs/mm | L/mm | s/mm | σs/MPa | σy/MPa | σcu/MPa | Te/(kN·m) | Ta/(kN·m) | Te/Ta |
|---|---|---|---|---|---|---|---|---|---|
| CBT-1 | 700×110×100×200 | 3 800 | 100 | 299.6 | 302.2 | 41.0 | 18.34 | 19.27 | 0.95 |
| CBT-2 | 700×110×100×200 | 3 800 | 80 | 299.6 | 302.2 | 35.5 | 18.20 | 17.88 | 1.02 |
| CBT-3 | 700×110×100×200 | 1 800 | 180 | 299.6 | 328.1 | 26.0 | 17.78 | 16.50 | 1.08 |
| CBT-4 | 700×110×100×200 | 1 800 | 130 | 299.6 | 328.1 | 32.0 | 18.52 | 19.78 | 0.94 |
| RCST-1 | 700×110×100×200 | 3 800 | 100 | — | 343.0 | 39.5 | 12.94 | 13.80 | 0.94 |
| RCST-2 | 700×110×100×200 | 3 800 | 80 | — | 343.0 | 37.6 | 11.24 | 12.78 | 0.88 |
| RCST-3 | 700×110×100×200 | 1 800 | 180 | — | 343.0 | 40.0 | 10.51 | 9.88 | 1.06 |
| RCST-4 | 700×110×100×200 | 1 800 | 130 | — | 343.0 | 36.6 | 9.07 | 9.24 | 0.98 |
| L/mm | wc/mm | hc/mm | ws/mm | hs/mm | ds/mm | 栓钉布置 |
|---|---|---|---|---|---|---|
| 4 000 | 800 | 120 | 100 | 200 | 16 | 单排 |
| 8 000 | 1 500 | 140 | 250 | 350 | 19 | 双排 |
| 12 000 | 2 200 | 150 | 400 | 500 | 19 | 双排 |
表2 部分足尺算例参数
Table 2 Partial full scale calculation parameters
| L/mm | wc/mm | hc/mm | ws/mm | hs/mm | ds/mm | 栓钉布置 |
|---|---|---|---|---|---|---|
| 4 000 | 800 | 120 | 100 | 200 | 16 | 单排 |
| 8 000 | 1 500 | 140 | 250 | 350 | 19 | 双排 |
| 12 000 | 2 200 | 150 | 400 | 500 | 19 | 双排 |

图5 组合钢梁与纯钢梁截面应力分布随荷载的变化规律对比(a)—腹板正应力分布; (b)—腹板剪应力分布; (c)—上翼缘正应力分布; (d)—上翼缘剪应力分布;(e)—下翼缘正应力分布; (f)—下翼缘剪应力分布.
Fig.5 Comparison of change law of stress distribution with load in cross?section of composite steel beam and steel beam

图6 组合梁混凝土板与纯混凝土板 τ - γ 对比、 T - θ′对比(a)—混凝土板上表面最大剪应力 τ -γ曲线对比; (b)— T - θ'曲线对比.
Fig.6 Comparison of τ - γ and T - θ′ between composite beam concrete slab and concrete slab
| 序号 | 公式 | 参考文献 | |
|---|---|---|---|
| 1 | Tu=Tc+Ts=3.089wc× | (8) | [ |
| 2 | Tu=αWtp σt+βσsyAsvlAcor/s α=1.10-0.25ρ, β=0.83+5.66ρ-5.36ρ2 | (9) | [ |
表3 工字钢-混凝土组合梁抗扭承载力计算公式
Table 3 Calculation formula for torsional bearing capacity of I?beam?concrete composite beams
| 序号 | 公式 | 参考文献 | |
|---|---|---|---|
| 1 | Tu=Tc+Ts=3.089wc× | (8) | [ |
| 2 | Tu=αWtp σt+βσsyAsvlAcor/s α=1.10-0.25ρ, β=0.83+5.66ρ-5.36ρ2 | (9) | [ |
| 1 | 聂建国,余志武.钢-混凝土组合梁在我国的研究及应用[J].土木工程学报,1999,32(2):3-8. |
| Nie Jian‑guo, Yu Zhi‑wu.Research and practice of composite steel‑concrete beams in China[J].China Civil Engineering Journal,1999,32(2):3-8. | |
| 2 | Wang Y C.Deflection of steel‑concrete composite beams with partial shear interaction[J].Journal of Structural Engineering,1998,124(10):1159-1165. |
| 3 | Ding F X, Liu J, Liu X M,et al.Flexural stiffness of steel‑concrete composite beams under positive moment[J].Steel and Composite Structures,2016,20(6):1369-1389. |
| 4 | Ding F X, Ding H, He C,et al.Method for flexural stiffness of steel‑concrete composite beams based on stiffness combination coefficients[J].Computers and Concrete,2022,29(3):127-144. |
| 5 | Ding F X, Liu J, Liu X M,et al.Flexural capacity of steel‑concrete composite beams under hogging moment[J].Advances in Civil Engineering,2019,2019:1-13. |
| 6 | 丁发兴,王恩,吕飞,等.考虑组合作用的钢-混凝土组合梁抗剪承载力[J].工程力学,2021,38(7):86-98. |
| Ding Fa‑xing, Wang En, Fei Lyu,et al.Composite action of steel‑concrete composite beams under lateral shear force[J].Engineering Mechanics,2021,38(7):86-98. | |
| 7 | Ollgaard J G, Slutter R G, Fisher J W.Shear strength of stud connectors in lightweight and normal‑weight concrete[J].AISC Engineering Journal,1971,8(2):55-64. |
| 8 | Ding F X, Ying X Y, Zhou L C,et al.Unified calculation method and its application in determining the uniaxial mechanical properties of concrete[J].Frontiers of Architecture and Civil Engineering in China,2011,5(3):381-393. |
| 9 | Uddin M A, Sheikh A H, Brown D,et al.Geometrically nonlinear inelastic analysis of steel‑concrete composite beams with partial interaction using a higher‑order beam theory[J].International Journal of Non-linear Mechanics,2018,100:34-47. |
| 10 | Jaafer A A, Kareem S L.Behavior of curved steel‑concrete composite beams under monotonic load[J].International Journal of Mathematical Engineering and Management Sciences,2020,5(6):1210-1233. |
| 11 | Liang X, Duan S J, Wang Y Y,et al.Experimental and theoretical study on the behavior of the laminated action of steel‑concrete composite beam in negative bending moment region[J].Advanced Steel Construction,2020,16(3):216-222. |
| 12 | 门朋飞.钢-混凝土组合梁负弯矩区受剪性能及其抗剪承载力计算方法研究[D].重庆:重庆大学,2021. |
| Peng‑fei Men.Study on shear performance and shear capacity calculation method of steel‑concrete composite girders in negative moment regions[D].Chongqing:Chongqing University,2021. | |
| 13 | Singh R K, Mallick S K.Experiments on steel‑concrete composite beams subjected to torsion and combined flexure and torion[J].India Concrete Journal,1977,51(1):24-30. |
| 14 | Ghosh B, Malick S K.Strength of steel‑concrete composite beams under combined flexure and torsion[J].India Concrete Journal,1979,53(2):48-53. |
| 15 | Hsu T C.Softened truss model theory for shear and torsion[J].ACI Structural Journal,1988,85(6):624-635. |
| 16 | 聂建国.钢-混凝土组合梁结构试验、理论与应用[M].北京:科学出版社,2005. |
| Nie Jian‑guo.Steel‑concrete composite beams structure:experiment,theory and application[M].Beijing:Science Press,2005. | |
| 17 | 聂建国,朱红超,罗玲,等.开口截面钢-混凝土组合梁受扭的试验分析[J].建筑结构学报,2002,23(2):48-54. |
| Nie Jian‑guo, Zhu Hong‑chao, Luo Ling,et al.Experimental analysis on composite steel‑concrete beams with open section under combined flexure and torsion[J].Journal of Building Structures,2002,23(2):48-54. | |
| 18 | Ding F X, Cao Z Y, Lyu F,et al.Practical design equations of the axial compressive capacity of circular CFST stub columns based on finite element model analysis incorporating constitutive models for high‑strength materials[J].Case Studies in Construction Materials,2022,16:e01115. |
| 19 | 聂建国,唐亮,朱林森.钢筋混凝土板式构件抗扭机理分析[J].清华大学学报(自然科学版),2006,46(6):760-764. |
| Nie Jian‑guo, Tang Liang, Zhu Lin‑sen.Analysis of reinforced concrete slabs subjected to pure torsion[J].Journal of Tsinghua University(Science and Technology),2006,46(6):760-764. | |
| 20 | 钢结构设计标准: [S].北京:中国建筑工业出版社,2017. |
| Standard for classification of steel structures: [S].Beijing:China Architecture and Building Press,2017. | |
| 21 | 孙训方,方孝淑,关来泰.材料力学[M].北京:高等教育出版社,2009. |
| Sun Xun‑fang, Fang Xiao‑shu, Guan Lai‑tai.Material mechanics[M].Beijing:Higher Education Press,2009. | |
| 22 | 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: [S].北京:中国建筑工业出版社,2015. |
| Ministry of Agriculture and Rural Affairs of teh Peoples’s Republic of China. Code for design of concrete structures: [S].Beijing:China Architecture and Building Press,2015. |
| [1] | 黄贤振, 于瑞, 姜智元, 荣治明. 考虑热误差的电主轴建模与可靠性全局灵敏度分析[J]. 东北大学学报(自然科学版), 2024, 45(5): 675-682. |
| [2] | 张东祥, 张弛, 范威, 郭立新. 人工锥体的尺寸对颈椎力学特性的影响[J]. 东北大学学报(自然科学版), 2023, 44(8): 1136-1143. |
| [3] | 安国青, 王蕊, 赵晖, 李铁英. 双钢板混凝土组合板在撞击荷载下的动力响应[J]. 东北大学学报(自然科学版), 2022, 43(8): 1192-1200. |
| [4] | 王连广, 蒙玉琪, 王梓晴. 预制压型钢板混凝土组合板和钢梁连接及其有限元分析[J]. 东北大学学报(自然科学版), 2022, 43(4): 575-581. |
| [5] | 陈小辉, 张珩, 刘明月, 侯东晓. 开孔碳纤维复合材料层合板的拉伸失效有限元分析[J]. 东北大学学报(自然科学版), 2022, 43(3): 397-403. |
| [6] | 张耀满, 李万鹏, 杨铭宇. 球头铣刀加工钛合金零件的铣削力特性[J]. 东北大学学报:自然科学版, 2020, 41(6): 852-857. |
| [7] | 李军超, 谢锋, 赵泽, 龚鹏程. 金属板材渐进成形的数值模拟及破裂预测[J]. 东北大学学报:自然科学版, 2019, 40(4): 488-494. |
| [8] | 冯乃诗, 王宏, 胡佛, 李康. 软体机器手纤维增强式三腔体结构设计与分析[J]. 东北大学学报:自然科学版, 2019, 40(10): 1461-1466. |
| [9] | 宋波, 王连广, 王春刚. 帽形加劲复杂卷边槽钢柱的稳定性能[J]. 东北大学学报:自然科学版, 2018, 39(1): 143-147. |
| [10] | 潘宏刚, 袁惠群, 赵天宇, 王光定. 基于汽轮机模拟叶轮的模态测试实验[J]. 东北大学学报:自然科学版, 2017, 38(9): 1298-1303. |
| [11] | 陈岩, 芦旭, 江鹏, 关振群. 影响螺纹副轴向力分布均匀性的关键因素分析[J]. 东北大学学报:自然科学版, 2017, 38(8): 1142-1147. |
| [12] | 卢晓红, 王福瑞, 路彦君, 高路丝. Inconel 718微铣削加工表面残余应力有限元仿真[J]. 东北大学学报:自然科学版, 2017, 38(2): 254-259. |
| [13] | 付彦铭, 于天彪, 王新, 王宛山. 犁式滑雪转弯膝关节软骨有限元分析[J]. 东北大学学报:自然科学版, 2017, 38(10): 1431-1435. |
| [14] | 闫玉涛, 钱晓林, 张毅博, 孙志礼. 滑动接触效应对裂纹尖端J积分值影响分析[J]. 东北大学学报:自然科学版, 2016, 37(12): 1744-1749. |
| [15] | 杨光, 张康生, 胡正寰. 螺杆压缩机阴转子定轴横轧成形可行性研究[J]. 东北大学学报:自然科学版, 2015, 36(12): 1785-1789. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||