参数寻优自适应重构特征的高压辊磨机运行故障诊断

doi:10.12068/j.issn.1005-3026.2025.20240087

摘要/Abstract

摘要：

高压辊磨机的运行环境复杂且信号易受到噪声污染，针对传统算法难以有效提取高压辊磨机故障特征以及随机共振系统参数选取困难的问题，提出了一种基于参数寻优自适应重构特征的高压辊磨机运行故障诊断方法.首先，采用集合经验模态分解(ensemble empirical mode decomposition, EEMD)算法将高压辊磨机振动信号分解成若干个本征模态函数(intrinsic mode function, IMF)分量；其次，结合相关系数与互信息构建混合判别准则，自适应地筛选出异常运行特征最强的分量信号进行重构；在此基础上，引入具有种群概率突变机制的樽海鞘群算法(salp swarm algorithm, SSA)，构建自适应的随机共振(stochastic resonance, SR)参数寻优策略；最后, 提出基于自适应选取分量重构信号的高压辊磨机运行故障诊断方法.仿真实验结果表明了所提方法的有效性.

关键词: 故障诊断, 集合经验模态分解, 樽海鞘群算法, 随机共振, 自适应策略

Abstract:

The operating environment of the high-pressure grinding roll is complicated， and the signal is easily polluted by noise. Traditional algorithms find it difficult to extract the fault characteristics of high-pressure grinding rolls effectively and select the parameters of the stochastic resonance system. To address these issues， an operation fault diagnosis method of high-pressure grinding roll based on adaptive reconstruction features with parameter optimization was proposed. First， the ensemble empirical mode decomposition （EEMD） method was employed to decompose the high-pressure grinding roll’s vibration signal into several intrinsic mode function （IMF） components. Secondly， the mixed criterion of correlation coefficient and mutual information was used to adaptively screen the component signals with the strongest abnormal operation characteristics and reconstruct them. Then， the salp swarm algorithm （SSA） was introduced to build the adaptive stochastic resonance （SR） parameter optimization mechanism by combining the population probabilistic mutation mechanism. Finally， an operation fault diagnosis algorithm of high-pressure grinding roll based on an adaptively selected component reconstruction signal was proposed. Simulation results verify the effectiveness of the proposed method.

Key words: fault diagnosis, ensemble empirical mode decomposition, salp swarm algorithm, stochastic resonance, adaptive strategy

中图分类号:

TD 50

孙洪硕, 张丹威, 徐泉, 柴天佑. 参数寻优自适应重构特征的高压辊磨机运行故障诊断[J]. 东北大学学报（自然科学版）, 2025, 46(11): 1-11.

Hong-shuo SUN, Dan-wei ZHANG, Quan XU, Tian-you CHAI. Operation Fault Diagnosis of High-Pressure Grinding Roll Using Adaptive Reconstruction Features with Parameter Optimization[J]. Journal of Northeastern University(Natural Science), 2025, 46(11): 1-11.

图/表 13

图1 故障诊断流程图

Fig.1 Fault diagnosis flowchart

图2 信号频谱图（a）—原始波形；（b）—傅里叶变换；（c）—包络谱.

Fig.2 Signal spectrum diagram

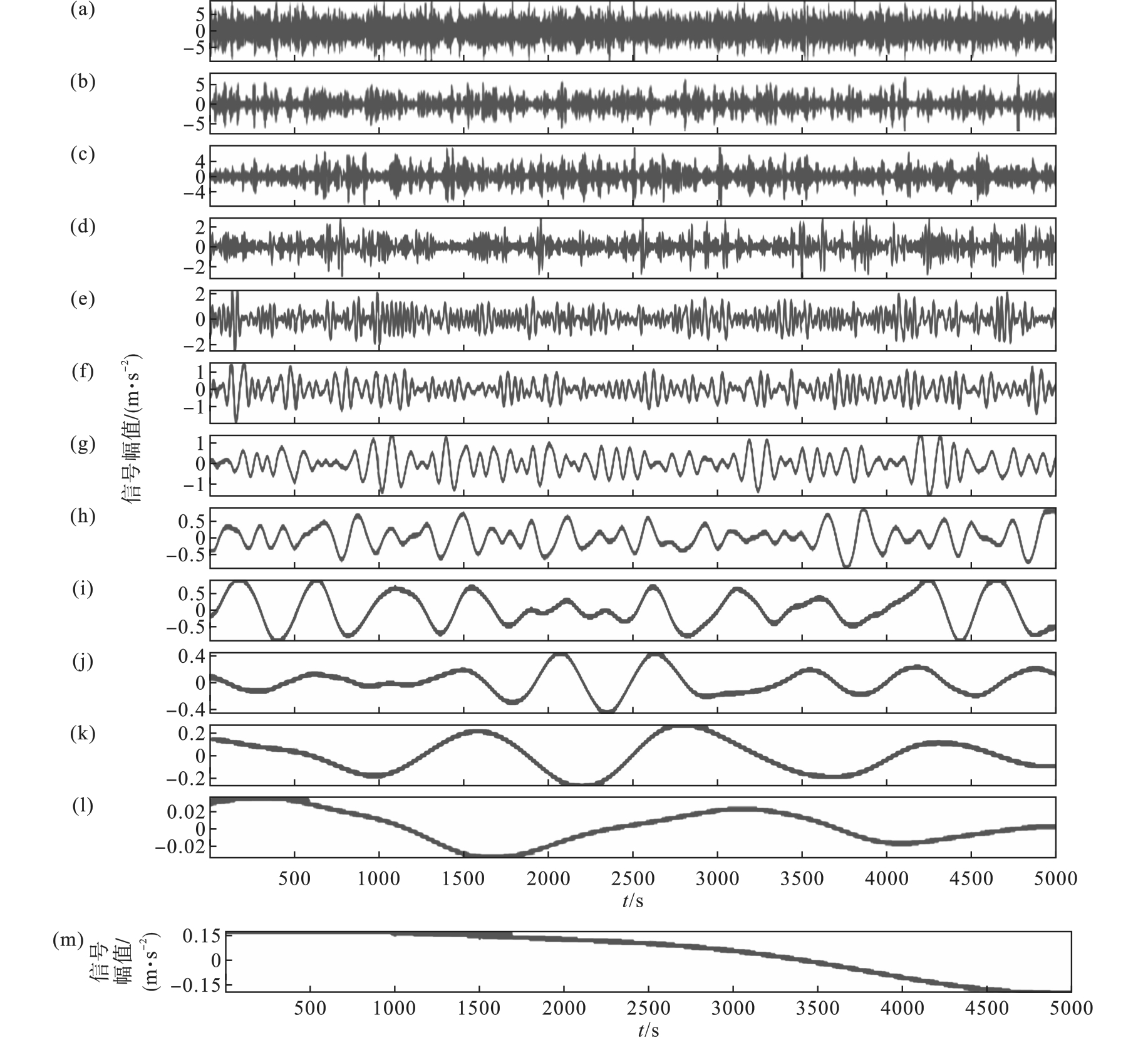
图3 原始仿真信号经过EEMD分解得到的IMF分量图（a）—IMF1分量；（b）—IMF2分量；（c）—IMF3分量；（d）—IMF4分量；（e）—IMF5分量；（f）—IMF6分量；（g）—IMF7分量；（h）—IMF8分量；（i）—IMF9分量；（j）—IMF10分量；（k）—IMF11分量；（l）—IMF12分量；（m）—残差余项.

Fig.3 IMF component diagram obtained from EEMD of original simulation signal

图4 IMF分量信号的判别指数R(p)

Fig.4 Discriminant index R(p) of IMF component signal

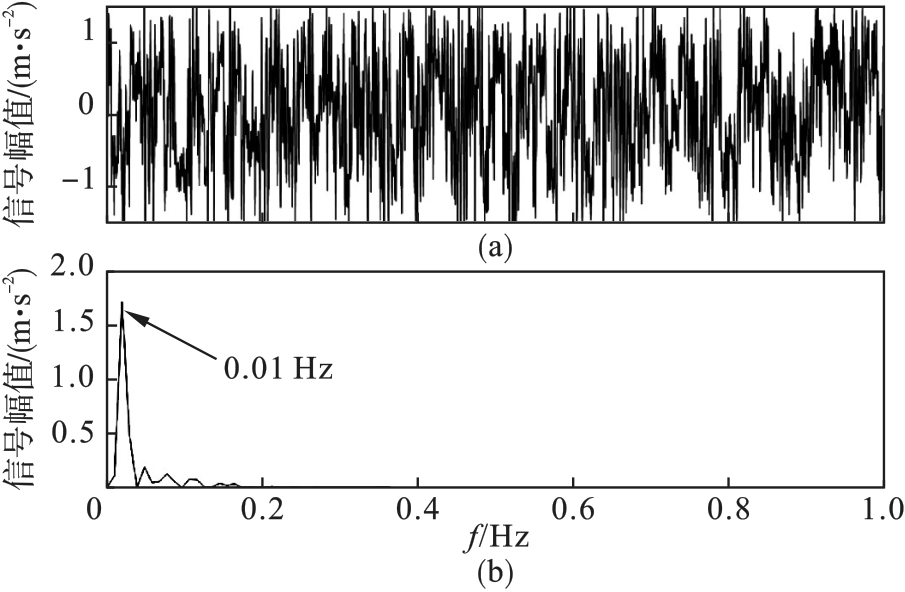
图5 重构信号经双稳随机共振系统时域波形图和频谱图（a）—时域波形图；（b）—频谱图.

Fig.5 Time-domain waveform and spectrum diagrams of reconstructed signal through bistable stochastic resonance system

图6 高压辊磨机振动信号传感器安装位置及采集装置（a）—现场设备；（b）—振动信号采集卡；（c）—振动信号存储.

Fig.6 Installation position and acquisition device of vibration signal sensor for high-pressure grinding roll

图7 高压辊磨机振动信号频谱图（a）—原始振动信号波形图；（b）—傅里叶变换波形图；（c）—包络谱图.

Fig.7 Spectrum diagram of vibration signal of high-pressure grinding roll

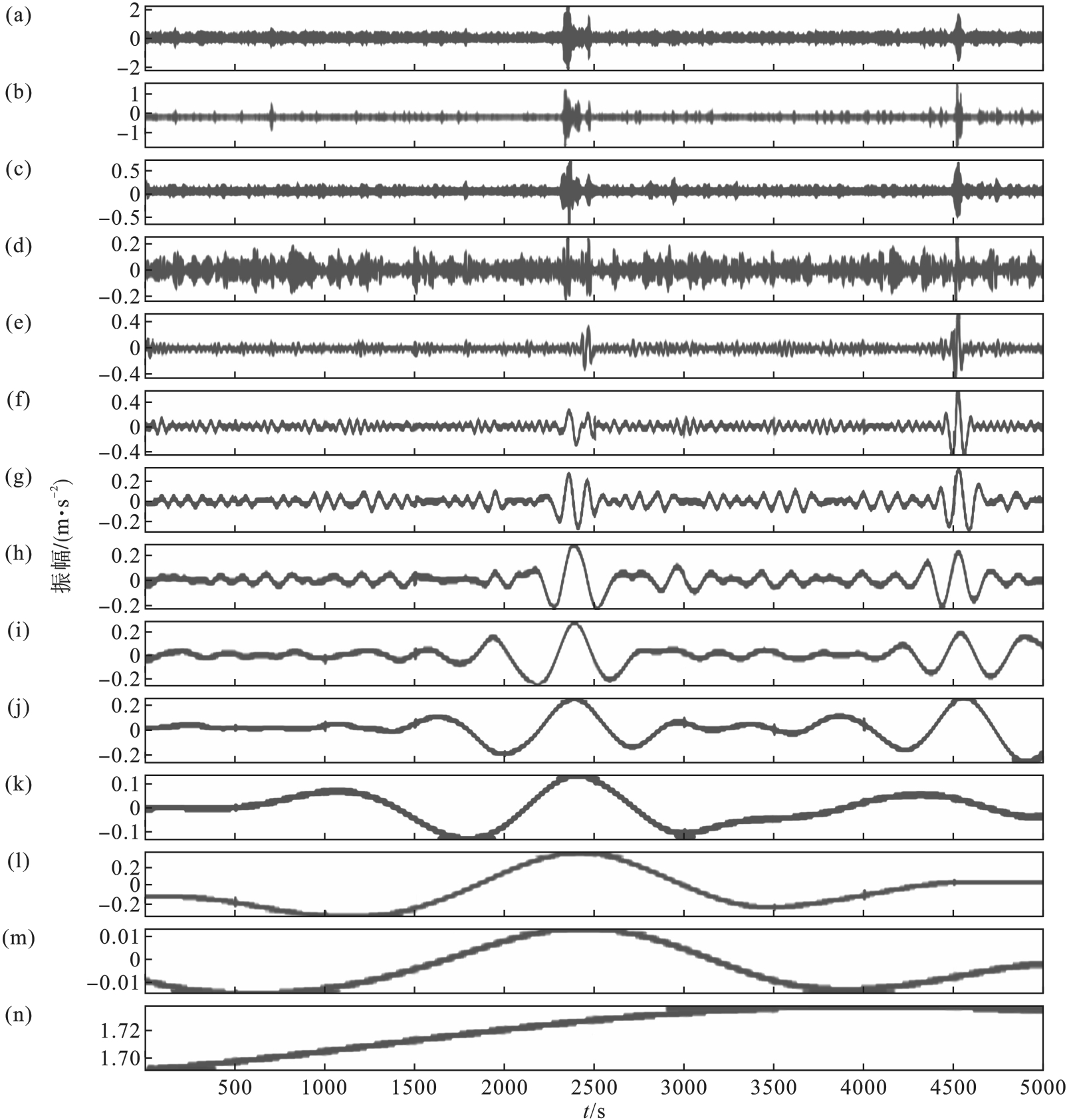
图8 原始振动信号经过EEMD分解的IMF分量图（a）—IMF1分量；（b）—IMF2分量；（c）—IMF3分量；（d）—IMF4分量；（e）—IMF5分量；（f）—IMF6分量；（g）—IMF7分量；（h）—IMF8分量；（i）—IMF9分量；（j）—IMF10分量；（k）—IMF11分量；（l）—IMF12分量；（m）—IMF13分量；（n）—残差余项.

Fig.8 IMF component diagram of original vibration signal after EEMD

图9 实际振动信号的IMF分量信号判别指数R(p)

Fig.9 IMF component signal discrimination index R(p) of actual vibration signal

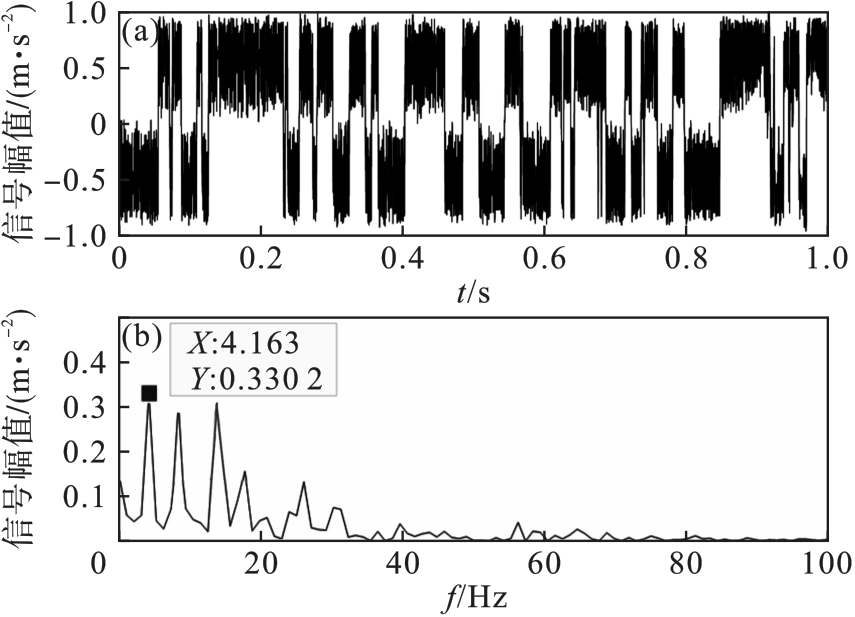
图10 蚁群优化随机共振系统的时域波形图和频谱图（a）—蚁群优化算法时域波形图；（b）—蚁群优化算法频谱图.

Fig.10 Time-domain waveform and spectrum diagrams of ant colony-optimized stochastic resonance system

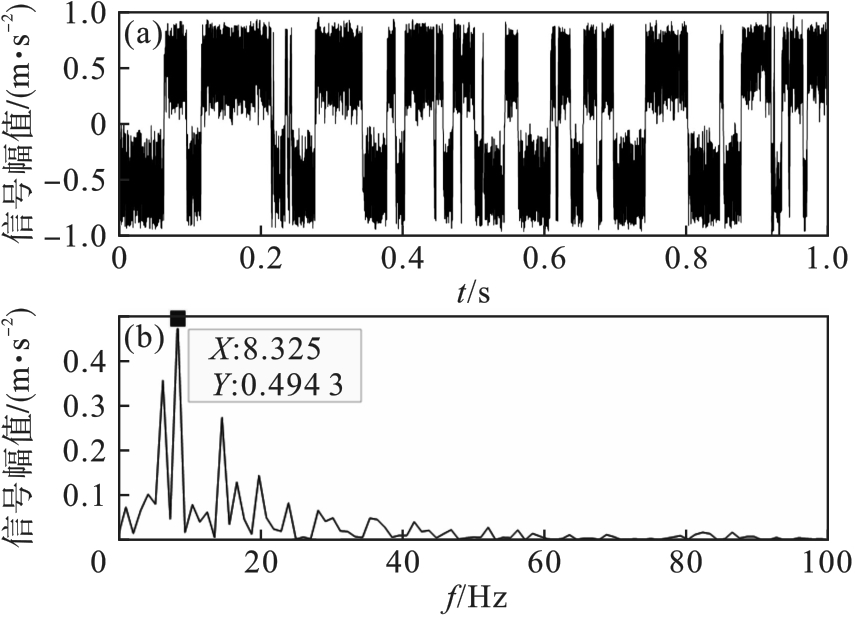
图11 粒子群优化随机共振系统时域波形图和频谱图（a）—粒子群优化算法时域波形图；（b）—粒子群优化算法频谱图.

Fig.11 Time-domain waveform and spectrum diagrams of particle swarm-optimized stochastic resonance system

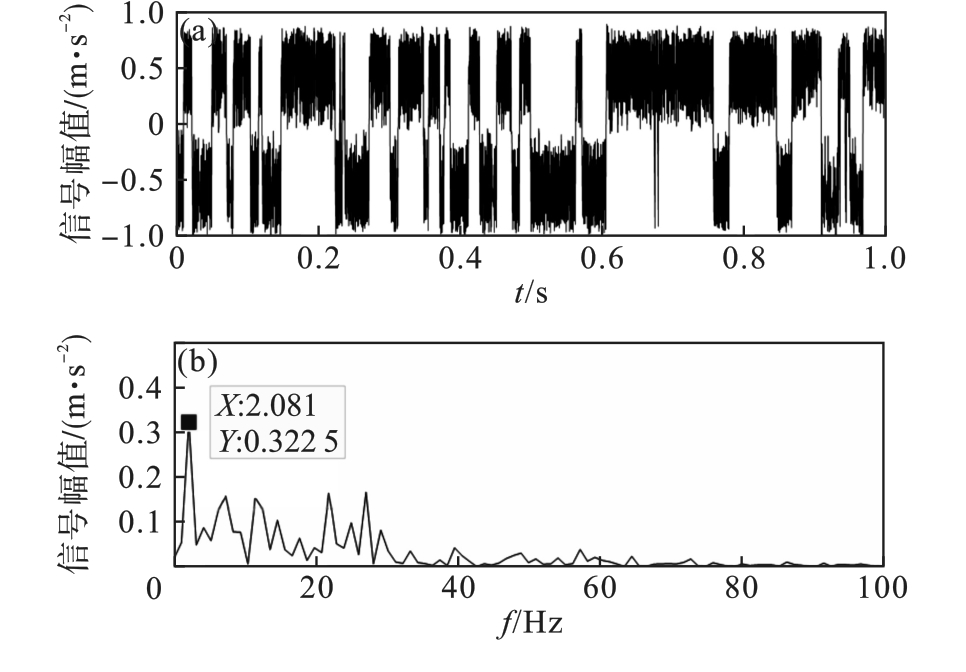
图12 本文优化随机共振系统的时域波形图和频谱图（a）—本文算法时域波形图；（b）—本文算法频谱图.

Fig.12 Time-domain waveform and spectrum diagrams of optimized stochastic resonance system in this paper

表1 3种方法对比结果

Table 1 Comparison results of three methods

方法

寻优

次数

初始种

群数/个

时间/s

特征

频率/Hz

参考文献 24

[1]	Coussat A， Rit S， Clackdoyle R， et al. Region-of-interest CT reconstruction using object extent and singular value decomposition［J］. IEEE Transactions on Radiation and Plasma Medical Sciences， 2022， 6（5）： 537-551.
[2]	Chai M Y， Gao Z Y， Li Y Q， et al. An approach for identifying corrosion damage from acoustic emission signals using ensemble empirical mode decomposition and linear discriminant analysis［J］. Measurement Science and Technology， 2022， 33（6）： 065018.
[3]	Smith J S. The local mean decomposition and its application to EEG perception data［J］. Journal of The Royal Society Interface， 2005， 2（5）：443-454.
[4]	Libanda B， Nkolola N B. An ensemble empirical mode decomposition of consecutive dry days in the Zambezi Riparian Region： implications for water management［J］. Physics and Chemistry of the Earth，（Parts A/B/C）， 2022， 126： 103147.
[5]	曹源，宋迪，胡小溪，等. 基于改进时域多尺度散布熵与支持向量机的转辙机故障诊断［J］. 电子学报， 2023， 51（1）： 117-127.
	Cao Yuan， Song Di， Hu Xiao-xi， et al. Fault diagnosis of railway point machine based on improved time-domain multiscale dispersion entropy and support vector machine［J］. Acta Electronica Sinica， 2023， 51（1）： 117-127.
[6]	Torres M E， Colominas M A， Schlotthauer G， et al. A complete ensemble empirical mode decomposition with adaptive noise［C］//2011 IEEE International Conference on Acoustics， Speech and Signal Processing （ICASSP）. Prague， 2011： 4144-4147.
[7]	Benzi R， Sutera A， Vulpiani A. The mechanism of stochastic resonance［J］. Journal of Physics A： Mathematical and General， 1981， 14（11）： L453-L457.
[8]	Peters K J H， Geng Z， Malmir K， et al. Extremely broadband stochastic resonance of light and enhanced energy harvesting enabled by memory effects in the nonlinear response.［J］. Physical Review Letters， 2021， 126（21）： 213901.
[9]	Qiao Z J， Lei Y G， Lin J， et al. Stochastic resonance subject to multiplicative and additive noise： the influence of potential asymmetries［J］. Physical Review E， 2016， 94（5）： 052214.
[10]	Su D X， Zheng R C， Nakano K， et al. On square-wave-driven stochastic resonance for energy harvesting in a bistable system［J］. AIP Advances， 2014， 4（11）： 117140.
[11]	Qiao Z J， Chen S， Lai Z H， et al. Harmonic-Gaussian double-well potential stochastic resonance with its application to enhance weak fault characteristics of machinery［J］. Nonlinear Dynamics， 2023， 111（8）： 7293 -7307.
[12]	孔德阳，彭华，马金全. 基于人工鱼群算法的自适应随机共振方法研究［J］.电子学， 2017， 45（8）： 1864-1872．
	Kong De-yang， Peng Hua， Ma Jin-quan. Adaptive stochastic resonance method based on artificial-fish swarm optimization［J］. Acta Electronica Sinica， 2017，45（8）： 1864-1872.
[13]	瞿铁，李詠侠，伏坤，等. 高压辊磨机用硬质合金柱钉的磨损和断裂行为［J］. 中国有色金属学报， 2024， 34（10）： 3394-3405.
	Qu Tie， Li Yong-xia， Fu Kun， et al. Wear and fracture behavior of cemented carbide column nails for high-pressure roller mills［J］. The Chinese Journal of Nonferrous Metals， 2024， 34（10）： 3394-3405.
[14]	范威，水沛，谢传东，等.基于Archard模型与DEM仿真的高压辊磨机磨损演化规律研究与优化［J］.金属矿山，2024（6）：173-180.
	Fan Wei， Shui Pei， Xie Chuan-dong， et al. Research and optimization of wear evolution law of high pressure roller mill based on archard model and DEM simulation［J］. Metal Mine， 2024（6）： 173-180.
[15]	Huang N E， Shen Z， Long S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proceedings of the Royal Society A： Mathematical， Physical and Engineering Sciences， 1998， 454（1971）： 903-995.
[16]	Cao Y， Zhang Y Z， Wen T， et al. Research on dynamic nonlinear input prediction of fault diagnosis based on fractional differential operator equation in high-speed train control system［J］. Chaos， 2019， 29（1）： 013130.
[17]	张敏，蔡振宇，包珊珊.基于EEMD-Hilbert和FWA-SVM的滚动轴承故障诊断方法［J］.西南交通大学学报， 2019， 54（3）： 633-639， 662.
	Zhang Min， Cai Zhen-yu， Bao Shan-shan. Fault diagnosis of rolling bearing based on EEMD-Hilbert and FWA-SVM［J］. Journal of Southwest Jiaotong University， 2019， 54（3）： 633-639， 662.
[18]	周平，刘记平.基于数据驱动多输出ARMAX建模的高炉十字测温中心温度在线估计［J］.自动化学报， 2018， 44（3）： 552-561.
	Zhou Ping， Liu Ji-ping. Data-driven multi-output ARMAX modeling for online estimation of central temperatures for cross temperature measuring in blast furnace ironmaking［J］. Acta Automatica Sinica， 2018， 44（3）： 552-561.
[19]	Qiao Z J， Pan Z R. SVD principle analysis and fault diagnosis for bearings based on the correlation coefficient ［J］. Measurement Science and Technology， 2015， 26（8）： 085014.
[20]	Kamimura R. Cost-conscious mutual information maximization for improving collective interpretation of multi-layered neural networks［J］. Neurocomputing， 2020， 409： 259-274.
[21]	张丹威，王晓东，黄国勇.相关系数SVD增强随机共振的单向阀故障诊断［J］.电子学， 2018， 46（11）：2696-2704.
	Zhang Dan-wei， Wang Xiao-dong， Huang Guo-yong. Check valve fault diagnosis with correlation coefficient SVD enhanced stochastic resonance［J］. Acta Electronica Sinica， 2018， 46（11）： 2696-2704.
[22]	牟竹青，冯早，黄国勇，等. 自适应随机共振和DEMD的单向阀早期故障诊断［J］. 机械科学与技术， 2018， 37（4）： 537-544.
	Mu Zhu-qing， Feng Zao， Huang Guo-yong， et al. Early fault diagnosis of check valve with adaptive stochastic resonance and DEMD［J］. Mechanical Science and Technology for Aerospace Engineering， 2018， 37（4）： 537-544.
[23]	李明宇，张丹威. 高压辊磨运行工况识别算法研究［J］.金属矿山， 2022（4）： 188-194.
	Li Ming-yu， Zhang Dan-wei. Research on conditions identification algorithm for high-pressure grinding roll［J］. Metal Mine， 2022（4）： 188-194.
[24]	Qiao Z J， Lei Y G， Li N P. Applications of stochastic resonance to machinery fault detection： a review and tutorial［J］. Mechanical Systems and Signal Processing， 2019， 122： 502-536.