
东北大学学报(自然科学版) ›› 2024, Vol. 45 ›› Issue (3): 430-438.DOI: 10.12068/j.issn.1005-3026.2024.03.016
收稿日期:2022-10-28
出版日期:2024-03-15
发布日期:2024-05-17
通讯作者:
王连广
作者简介:高海洋(1996-),女,辽宁沈阳人,东北大学博士研究生基金资助:
Hai-yang GAO, Lian-guang WANG( ), Bai-ling CHEN
), Bai-ling CHEN
Received:2022-10-28
Online:2024-03-15
Published:2024-05-17
Contact:
Lian-guang WANG
About author:WANG Lian-guang, E-mail: wanglianguang@mail.neu.edu.cn摘要:
以85个FRP管-混凝土-钢管双壁空心柱(double‐skin tubular column,DSTC)轴压试验数据作为统计样本,评估了几种现有FRP约束混凝土强度模型,最终选择Teng模型进行可靠性分析,并确定了强度模型误差和构件抗力的最佳概率分布.运用JC法对DSTC进行可靠度计算.结果表明:可靠指标随着钢管强度、中空率和含钢率的提高而升高,而对混凝土强度的变化不敏感.FRP约束应力的增加会导致可靠指标的下降.基于可靠指标目标3.7,提出一个适用于DSTC的抗力分项系数表达式.
中图分类号:
高海洋, 王连广, 陈百玲. 轴压下FRP管-混凝土-钢管组合柱可靠性分析[J]. 东北大学学报(自然科学版), 2024, 45(3): 430-438.
Hai-yang GAO, Lian-guang WANG, Bai-ling CHEN. Reliability Analysis of FRP-Concrete-Steel Tubular Composite Column Under Axial Compression[J]. Journal of Northeastern University(Natural Science), 2024, 45(3): 430-438.
| 数据来源 | 试件数量 | Do /mm | Ds /mm | ts /mm | fco /MPa | fys/MPa | FRP类型 |
|---|---|---|---|---|---|---|---|
| 文献[ | 6 | 152.5 | 76.1 | 3.2 | 39.64 | 352.67 | GFRP |
| 文献[ | 18 | 152.5 | 42~115 | 2.1~5.2 | 36.7~46.7 | 337.8~406.2 | GFRP |
| 文献[ | 8 | 194.6~195.3 | 114/140 | 2.5~8.16 | 29.3~32.5 | 313~363 | GFRP/CFRP |
| 文献[ | 6 | 401.0/402.0 | 245.8/323.6 | 8.0/9.3 | 29.3~40.1 | 307.2~316.3 | GFRP |
| 文献[ | 14 | 152.5 | 60.3~114.3 | 3.2~6.0 | 49.8/113.8 | 314.2~459.4 | AFRP/CFRP |
| 文献[ | 10 | 152.5 | 60.3~114.3 | 3.2~6.0 | 96.2 | 318.3~446.4 | GFRP |
| 文献[ | 12 | 204.4~320.0 | 120~219 | 4.5~6.0 | 40.9~104.4 | 319.4~419.5 | GFRP |
| 文献[ | 11 | 100 | 48 | 1.5~3.0 | 35.6~40.0 | 350.0~471.7 | CFRP |
表1 FRP管-混凝土-钢管组合柱试验数据
Table 1 Test data of FRP?concrete?steel DSTCs
| 数据来源 | 试件数量 | Do /mm | Ds /mm | ts /mm | fco /MPa | fys/MPa | FRP类型 |
|---|---|---|---|---|---|---|---|
| 文献[ | 6 | 152.5 | 76.1 | 3.2 | 39.64 | 352.67 | GFRP |
| 文献[ | 18 | 152.5 | 42~115 | 2.1~5.2 | 36.7~46.7 | 337.8~406.2 | GFRP |
| 文献[ | 8 | 194.6~195.3 | 114/140 | 2.5~8.16 | 29.3~32.5 | 313~363 | GFRP/CFRP |
| 文献[ | 6 | 401.0/402.0 | 245.8/323.6 | 8.0/9.3 | 29.3~40.1 | 307.2~316.3 | GFRP |
| 文献[ | 14 | 152.5 | 60.3~114.3 | 3.2~6.0 | 49.8/113.8 | 314.2~459.4 | AFRP/CFRP |
| 文献[ | 10 | 152.5 | 60.3~114.3 | 3.2~6.0 | 96.2 | 318.3~446.4 | GFRP |
| 文献[ | 12 | 204.4~320.0 | 120~219 | 4.5~6.0 | 40.9~104.4 | 319.4~419.5 | GFRP |
| 文献[ | 11 | 100 | 48 | 1.5~3.0 | 35.6~40.0 | 350.0~471.7 | CFRP |
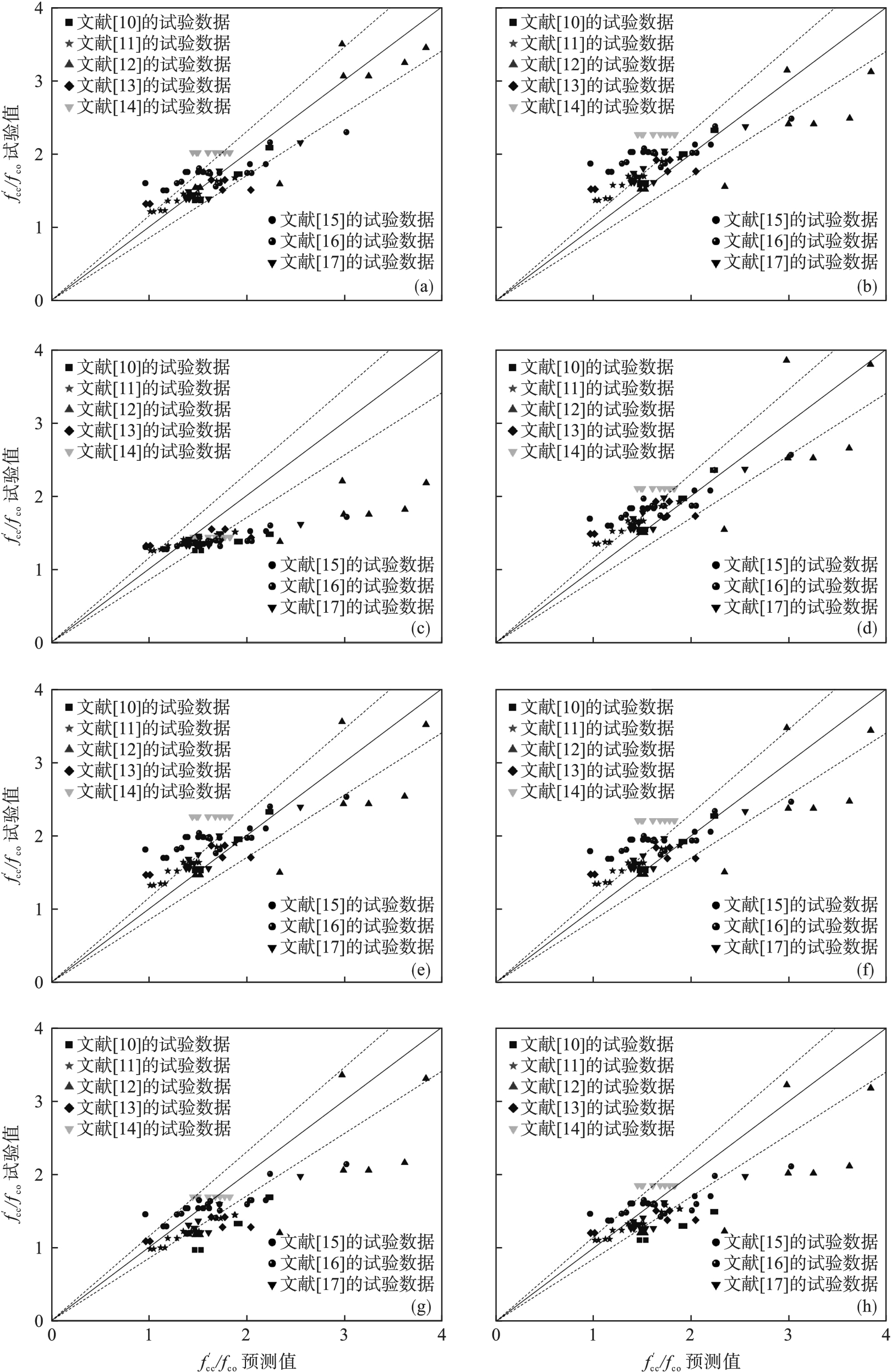
图2 不同强度模型的计算结果对比(a)—Teng等的模型; (b)—Lignola等的模型; (c)—Harries等的模型; (d)—Marques等的模型;(e)—Binici的模型; (f)—Xiao等的模型; (g)—Yu等的模型; (h)—Pham等的模型.
Fig.2 Comparison of ultimate strengths from different models
| 模型 | 极限强度 | AV | SD | CV |
|---|---|---|---|---|
| Teng等[ | 0.987 | 0.124 | 0.127 | |
| Lignola等[ | 0.893 | 0.117 | 0.130 | |
| Yu等[ | 1.184 | 0.163 | 0.137 | |
| Marques等[ | 0.913 | 0.118 | 0.128 | |
| Binici[ | 0.907 | 0.119 | 0.130 | |
| Xiao等[ | 0.919 | 0.123 | 0.132 | |
| Harries等[ | 1.211 | 0.196 | 0.161 | |
| Pham等[ | 1.139 | 0.156 | 0.137 |
表2 现有FRP约束混凝土强度模型计算结果
Table 2 Calculation results of strength models of existing FRP?confined concrete
| 模型 | 极限强度 | AV | SD | CV |
|---|---|---|---|---|
| Teng等[ | 0.987 | 0.124 | 0.127 | |
| Lignola等[ | 0.893 | 0.117 | 0.130 | |
| Yu等[ | 1.184 | 0.163 | 0.137 | |
| Marques等[ | 0.913 | 0.118 | 0.128 | |
| Binici[ | 0.907 | 0.119 | 0.130 | |
| Xiao等[ | 0.919 | 0.123 | 0.132 | |
| Harries等[ | 1.211 | 0.196 | 0.161 | |
| Pham等[ | 1.139 | 0.156 | 0.137 |
| 设计参数 | 均值系数 | 变异系数 | 概率分布类型 |
|---|---|---|---|
| FRP壁厚tFRP | 1 | 0.02 | 正态 |
| 混凝土外径Do | 1 | 0.01 | 正态 |
| 混凝土面积Ac | 1 | 0.05 | 正态 |
| 钢管面积As | 1 | 0.05 | 正态 |
| 恒荷载SG | 1.060 | 0.070 | 正态 |
| 办公楼活荷载SQO | 0.524 | 0.288 | 极值I型 |
| 住宅楼活荷载SQR | 0.644 | 0.230 | 极值I型 |
表3 设计参数不确定系数
Table 3 Uncertainty coefficient of design parameters
| 设计参数 | 均值系数 | 变异系数 | 概率分布类型 |
|---|---|---|---|
| FRP壁厚tFRP | 1 | 0.02 | 正态 |
| 混凝土外径Do | 1 | 0.01 | 正态 |
| 混凝土面积Ac | 1 | 0.05 | 正态 |
| 钢管面积As | 1 | 0.05 | 正态 |
| 恒荷载SG | 1.060 | 0.070 | 正态 |
| 办公楼活荷载SQO | 0.524 | 0.288 | 极值I型 |
| 住宅楼活荷载SQR | 0.644 | 0.230 | 极值I型 |
| 材料参数 | 钢材 | 材料参数 | 混凝土 | FRP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q235 | Q345 | C40 | C50 | C60 | C70 | C80 | ||||
| fyk/MPa | 235( 225( | 345( 335( | fck/MPa | 26.8 | 32.4 | 38.5 | 44.5 | 50.2 | — | |
| fys/MPa | 215( 205( | 305( 295( | fco/MPa | 19.1 | 23.1 | 27.5 | 31.8 | 35.9 | — | |
| 均值系数 | 1.08 | 1.09 | 均值系数 | 1.342 | 1.337 | 1.332 | 1.292 | 1.262 | 1.1 | |
| 变异系数 | 0.08 | 0.07 | 变异系数 | 0.156 | 0.149 | 0.141 | 0.121 | 0.101 | 0.083 | |
| 概率分布类型 | 对数正态 | 概率分布类型 | 正态 | 威布尔 | ||||||
表4 材料参数不确定系数
Table 4 Uncertainty coefficient of material parameters
| 材料参数 | 钢材 | 材料参数 | 混凝土 | FRP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q235 | Q345 | C40 | C50 | C60 | C70 | C80 | ||||
| fyk/MPa | 235( 225( | 345( 335( | fck/MPa | 26.8 | 32.4 | 38.5 | 44.5 | 50.2 | — | |
| fys/MPa | 215( 205( | 305( 295( | fco/MPa | 19.1 | 23.1 | 27.5 | 31.8 | 35.9 | — | |
| 均值系数 | 1.08 | 1.09 | 均值系数 | 1.342 | 1.337 | 1.332 | 1.292 | 1.262 | 1.1 | |
| 变异系数 | 0.08 | 0.07 | 变异系数 | 0.156 | 0.149 | 0.141 | 0.121 | 0.101 | 0.083 | |
| 概率分布类型 | 对数正态 | 概率分布类型 | 正态 | 威布尔 | ||||||
| 1 | Teng J G, Huang Y L, Lam L,et al.Theoretical model for fiber‐reinforced polymer‐confined concrete[J].Journal of Composites for Construction,2007,11(2):201-210. |
| 2 | Teng J G, Jiang T, Lam L,et al.Refinement of a design‐oriented stress‐strain model for FRP‐confined concrete[J].Journal of Composites for Construction,2009,13(4):269-278. |
| 3 | Lignola G P, Prota A, Manfredi G,et al.Unified theory for confinement of RC solid and hollow circular columns[J].Composites Part B,2008,39(7/8):1151-1160. |
| 4 | Yu T, Teng J G, Wong Y L.Stress‐strain behavior of concrete in hybrid FRP‐concrete‐steel double‐skin tubular columns[J].Journal of Structural Engineering,2010,136(4):379-389. |
| 5 | Li Y L, Teng J G, Zhao X L,et al.Theoretical model for seawater and sea sand concrete‐filled circular FRP tubular stub columns under axial compression[J].Engineering Structures,2018,160:71-84. |
| 6 | Baji H, Ronagh H R, Li C Q.Probabilistic assessment of FRP‑confined reinforced concrete columns[J].Composite Structures,2016,153:851-865. |
| 7 | 王慧青,张大山,林旭华,等.碳纤维增强复材加固钢筋混凝土轴压圆柱可靠度评估与规范评价[J].工业建筑,2021,51(6):206-211. |
| Wang Hui‐qing, Zhang Da‐shan, Lin Xu‐hua,et al.Reliability evaluation and specification discussion of CFRP reinforced concrete circular columns under axial loads[J].Industrial Construction,2021,51(6):206-211. | |
| 8 | Shali M G, Naderpour H A.Reliability‐based approach and code calibration of FRP‑confined rectangular RC columns subjected to concentric loading[J].Journal of Building Engineering,2021,44:102672. |
| 9 | Harries K A, Carey S A.Shape and “gap” effects on the behavior of variably confined concrete[J].Cement and Concrete Research,2003,33(6):881-890. |
| 10 | 滕锦光,余涛,黄玉龙,等.FRP管-混凝土-钢管组合柱力学性能的试验研究和理论分析[J].建筑钢结构进展,2006,8(5):1-7. |
| Teng Jin‐guang, Yu Tao, Huang Yu‐long,et al.Behavior of hybrid FRP‐concrete‐steel tubular columns:experimental and theoretical studies[J].Progress in Steel Building Structures,2006,8(5):1-7. | |
| 11 | Wong Y L, Yu T, Teng J G,et al.Behavior of FRP‑confined concrete in annular section columns[J].Composites Part B:Engineering,2008,39(3):451-466. |
| 12 | 钱稼茹,刘明学.FRP-混凝土-钢双壁空心管短柱轴心抗压试验研究[J].建筑结构学报,2008,29(2):104-113. |
| Qian Jia‐ru, Liu Ming‐xue.Experimental investigation of FRP‐concrete‐steel double‐skin tubular stubs under axial compressive loading[J].Journal of Building Structure,2008,29(2):104-113. | |
| 13 | Xie P, Yu T, Wong Y L,et al.Compressive behavior of large‐scale hybrid FRP‐concrete‐steel double‐skin tubular columns[J].Advanced Materials Research,2011,243:1138-1144. |
| 14 | Fanggi B A L, Ozbakkaloglu T.Compressive behavior of aramid FRP‐HSC‐steel double‐skin tubular columns[J].Construction and Building Materials,2013,48:554-565. |
| 15 | Fanggi B A L, Ozbakkaloglu T.Behavior of hollow and concrete‐filled FRP‐HSC and FRP‐HSC‐steel composite columns subjected to concentric compression[J].Advances in Structural Engineering,2015,18(5):715-738. |
| 16 | Zhang B, Teng J G, Yu T.Compressive behavior of double‐skin tubular columns with high‐strength concrete and a filament‐wound FRP tube[J].Journal of Composites for Construction,2017,21(5):04017029. |
| 17 | Salman W D, Mansor A A.Confinement of concrete in double skin tubular members under axial compression loads[J].Asian Journal of Civil Engineering,2021,22(3):431-442. |
| 18 | Marques S P C, Marques D C S C, da Silva J L,et al.Model for analysis of short columns of concrete confined by fiber‐reinforced polymer[J].Journal of Composites for Construction,2004,8(4):332-340. |
| 19 | Binici B.An analytical model for stress‐strain behavior of confined concrete[J].Engineering Structures,2005,27(7):1040-1051. |
| 20 | Xiao Q G, Teng J G, Yu T.Behavior and modeling of confined high‐strength concrete[J].Journal of Composites for Construction,2010,14(3):249-259. |
| 21 | Harries K A, Kharel G.Behavior and modeling of concrete subject to variable confining pressure[J].Materials Journal,2002,99(2):180-189. |
| 22 | Pham T M, Hadi M N S.Confinement model for FRP confined normal‐and high‐strength concrete circular columns[J].Construction and Building Materials,2014,69:83-90. |
| 23 | 中华人民共和国住房和城乡建设部. 纤维增强复合材料工程应用技术标准: [S].北京:中国计划出版社,2020. |
| China Ministry of Housing and Urban‑Rural Development. Technical standard for fiber reinforced polymer (FRP) in construction: [S].Beijing:China Planning Press,2020. | |
| 24 | 中华人民共和国住房和城乡建设部. 建筑结构可靠性设计统一标准: [S].北京:中国建筑工业出版社,2018. |
| China Ministry of Housing and Urban‐Rural Development. Unified standard for reliability design of building structures: [S].Beijing:China Architecture & Building Press,2018. | |
| 25 | 康玉梅,李佳其,刘子傲,等.基于概率密度演化方法的装配式箱涵构件可靠度研究[J].东北大学学报(自然科学版),2021,42(12):1782-1789. |
| Kang Yu‐mei, Li Jia‐qi, Liu Zi‐ao,et al.Reliability study of prefabricated box culvert components based on probability density evolution method[J].Journal of Northeastern University(Natural Science),2021,42(12):1782-1789. |
| [1] | 王海艳, 武晔, 付麒麟, 周秩同. 碳纤维复合材料螺旋铣孔细观切削力分析[J]. 东北大学学报(自然科学版), 2023, 44(7): 982-988. |
| [2] | 高雁鹏, 陈文俊. 沈阳市内五区开发强度时空演变及影响因素研究[J]. 东北大学学报(自然科学版), 2023, 44(5): 743-751. |
| [3] | 张路路, 范俊, 金光, 张昆. 层次期望提高航天器抗辐射等效试验方法[J]. 东北大学学报(自然科学版), 2022, 43(9): 1250-1255. |
| [4] | 王海艳, 金天, 周秩同, 付麒麟. 碳纤维增强复合材料螺旋铣孔的临界轴向力模型[J]. 东北大学学报(自然科学版), 2022, 43(2): 214-220. |
| [5] | 曹汝男, 孙志礼, 郭凡逸, 王健. 基于Kriging和Monte Carlo的动态可靠性算法[J]. 东北大学学报(自然科学版), 2021, 42(5): 658-664. |
| [6] | 刘博林, 谢里阳. 一种改进的全局可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(7): 943-948. |
| [7] | 于震梁, 孙志礼, 张毅博, 王健. 一种自适应PC-Kriging模型的结构可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(5): 667-672. |
| [8] | 曹汝男, 孙志礼, 张毅博, 王健. 基于主动学习的复杂机械结构的可靠性分析[J]. 东北大学学报:自然科学版, 2020, 41(2): 223-228. |
| [9] | 张毅博, 孙志礼, 闫玉涛, 王健. 一种基于失效概率相对误差估计的可靠性分析方法[J]. 东北大学学报:自然科学版, 2020, 41(2): 229-234. |
| [10] | 于震梁, 孙志礼, 曹汝男, 张毅博. 基于PC-Kriging模型与主动学习的齿轮热传递误差可靠性分析[J]. 东北大学学报:自然科学版, 2019, 40(12): 1750-1754. |
| [11] | 赵琪, 刘抚英. 基于修正产业辐射强度模型的辽宁省创意产业辐射动态研究[J]. 东北大学学报:自然科学版, 2019, 40(10): 1510-1516. |
| [12] | 侯雯峪, 王连广. 超载下预应力CFRP布加固腐蚀钢梁抗弯性能试验[J]. 东北大学学报:自然科学版, 2018, 39(9): 1342-1347. |
| [13] | 杨佳, 王连广. 内嵌CFRP板条加固超载损伤钢筋混凝土梁试验研究[J]. 东北大学学报:自然科学版, 2018, 39(6): 907-912. |
| [14] | 朱广山, 朱浮声, 盛国华. 预应力CFRP与钢板复合加固T梁抗弯性能试验[J]. 东北大学学报:自然科学版, 2018, 39(4): 594-598. |
| [15] | 涂宏茂, 孙志礼, 姬广振, 钱云鹏. 考虑失效模式相关性的机械系统可靠性分析[J]. 东北大学学报:自然科学版, 2017, 38(10): 1453-1458. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||