含局部缺陷的圆柱滚子轴承动力学建模与振动分析

doi:10.12068/j.issn.1005-3026.2025.20240108

摘要/Abstract

摘要：

为了分析滚道凹槽对圆柱滚子轴承动力学性能和振动特性的影响，以牵引电机圆柱滚子轴承为研究对象，建立具有波纹状凹槽的圆柱滚子轴承轴电流损伤模型.首先，采用分段函数描述由轴承滚道局部缺陷引起的附加位移，建立轴承局部缺陷损伤模型；其次，基于圆柱滚子轴承弹簧-质量简化模型，建立考虑滚道缺陷的轴承动力学模型；最后，通过仿真和实验研究了不同损伤程度对轴承振动特性及轴承载荷分布的影响规律，验证所建轴承模型的可靠性.结果表明，该模型有效反映了轴电流损伤引起的冲击激励和周期性变化规律，随着局部缺陷损伤程度的增加，轴承的振动响应和载荷分布波动加剧，轴承转动稳定性降低.

关键词: 圆柱滚子轴承, 损伤模型, 局部缺陷, 动力学, 振动响应

Abstract:

To analyze the influence of the raceway groove on the dynamic performance and vibration characteristics of cylindrical roller bearings， the cylindrical roller bearings of the traction motor were taken as the research object， and the shaft current damage model of the cylindrical roller bearings with a corrugated groove was established. Firstly， the additional displacement caused by the local defect of the bearing raceway was described by the piecewise function， and the damage model of the local defect of the bearings was established. Secondly， based on the simplified spring-mass model of cylindrical roller bearings， the bearing dynamic model considering raceway defects was established. Finally， through simulation and experiment， the influence of different damage degrees on bearing vibration characteristics and bearing load distribution was studied， and the reliability of the developed bearing model was determined. The results show that the bearing model effectively reflects the impact excitation and periodic change law caused by shaft current damage. With the increase of local defect damage degree， the vibration response and load distribution fluctuation of the bearings constantly increase， and the rotation of the bearings tends to be unstable.

Key words: cylindrical roller bearing, damage model, local defect, dynamics, vibration response

中图分类号:

TH 133.3

李小彭, 李雪东, 刘彬, 李柏涛. 含局部缺陷的圆柱滚子轴承动力学建模与振动分析[J]. 东北大学学报（自然科学版）, 2025, 46(11): 73-81.

Xiao-peng LI, Xue-dong LI, Bin LIU, Bai-tao LI. Dynamic Modeling and Vibration Analysis of Cylindrical Roller Bearings with Local Defects[J]. Journal of Northeastern University(Natural Science), 2025, 46(11): 73-81.

图/表 21

图1 轴承局部缺陷

Fig.1 Local defects in bearings

图2 分段函数示意图

Fig.2 Schematic diagram of piecewise function

图3 H1损伤接触图

Fig.3 H1 damage contact diagram

图4 H1损伤三维模型图

Fig.4 3D model diagram of H1 damage

图5 滚子与缺陷位置示意图

Fig.5 Schematic diagram of roller and defect location

图6 H3损伤接触图.

Fig.6 H3 damage contact diagram

图7 H3损伤三维模型图

Fig.7 3D model diagram of H3 damage

图8 轴承模型图（a）—轴承图；（b）—示意图.

Fig.8 Bearing model diagram

表 1 N205EM轴承参数

Table 1 N205EM bearing parameters

参数	符号	单位	数值
外圈外径	D_1o	mm	52
内圈外径	D_1i	mm	34
外圈内径	D_2o	mm	46
内圈内径	D_2i	mm	25
滚子直径	D_b	mm	6
滚子长度	L₁	mm	10
滚子数量	Z	个	13
轴承节圆直径	D_p	mm	40

图9 轴承在X方向的振动响应（a）—X方向加速度仿真结果；（b）—X方向加速度实验结果.

Fig.9 Vibration response of bearings in X direction

图10 轴承在Y方向的振动响应（a）—Y方向加速度仿真结果；（b）—Y方向加速度实验结果.

Fig.10 Vibration response of bearings in Y direction

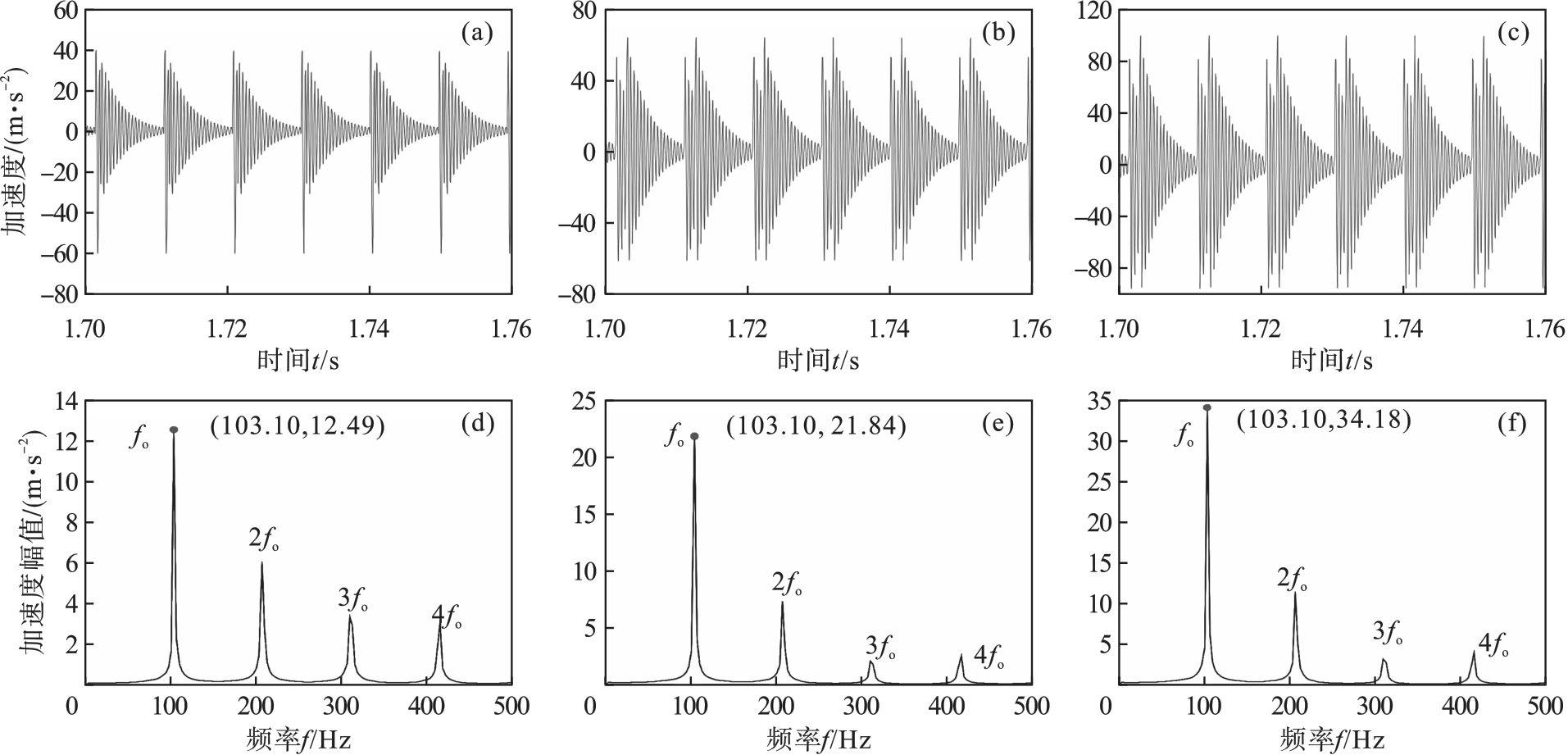
图11 不同损伤宽度的轴承动力学响应（a）—L=1 mm时的时域图；（b）—L=2 mm时的时域图；（c）—L=3 mm时的时域图；（d）—L=1 mm时的包络谱；（e）—L=2 mm时的包络谱；（f）—L=3 mm时的包络谱.

Fig.11 Dynamic response of bearings with different damage widths

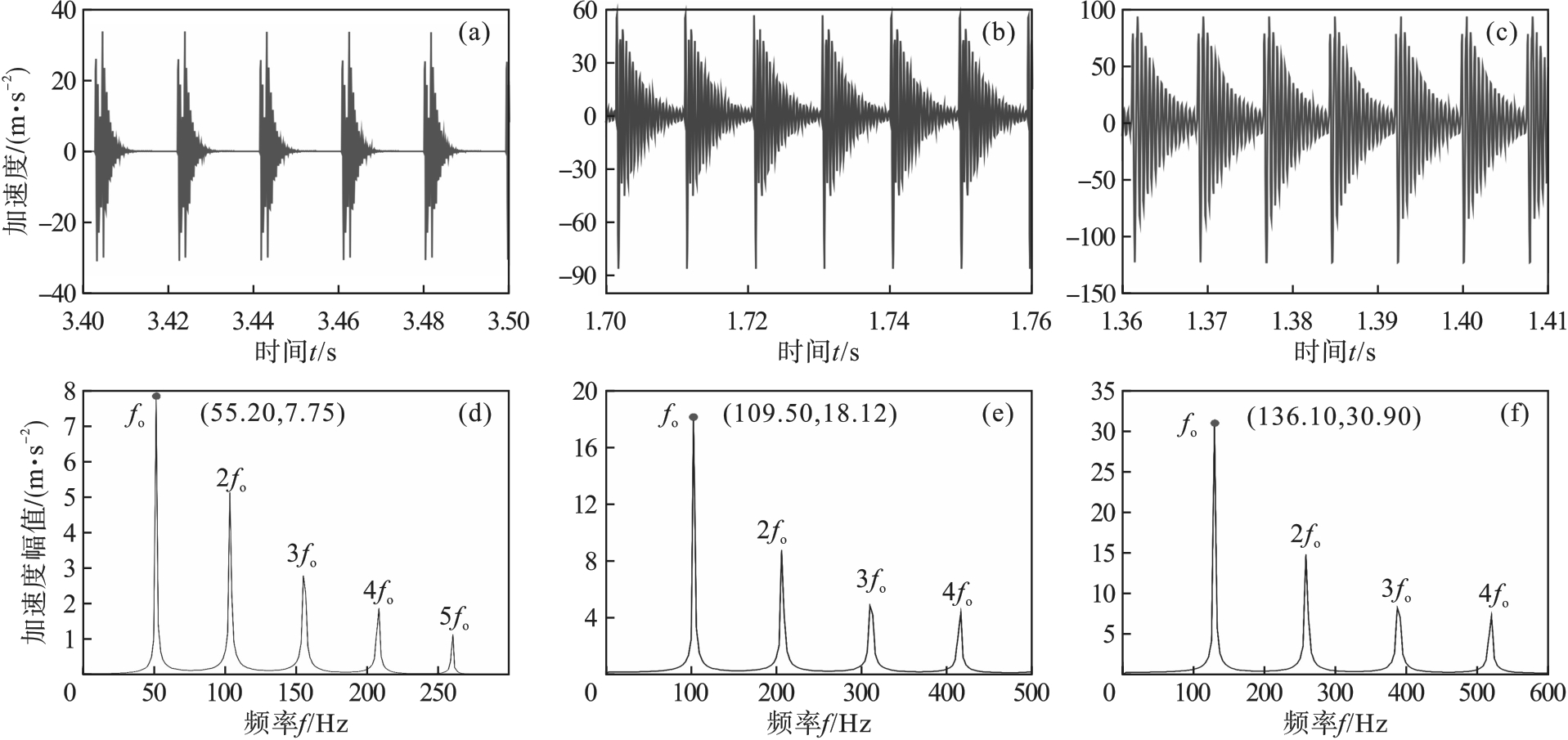
图12 不同转速的损伤轴承动力学响应（a）—n=600 r/min时的时域图；（b）—n=1 200 r/min时的时域图；（c）—n=1 500 r/min时的时域图；（d）—n=600 r/min的包络谱；（e）—n=1 200 r/min的包络谱；（f）—n=1 500 r/min的包络谱.

Fig.12 Dynamic response of damaged bearings at different rotating speeds

图13 损伤轴承的接触力

Fig.13 Contact force o f damaged bearings

图14 损伤程度对轴承接触力的影响

Fig.14 Influence of damage degree on bearing

图15 轴承转子实验台

Fig.15 Bearing rotor test bench

图16 轴承外圈故障（a）—L=1 mm；（b）—L=2 mm；（c）—L=3 mm.

Fig.16 Bearings’ outer ring fault

图17 600 r/min时轴承外圈故障状态动力学响应

Fig.17 Dynamic response of bearings’ outer ring

图18 1 200 r/min时轴承外圈故障状态动力学响应

Fig.18 Dynamic response of bearings’ outer ring

图19 1 500 r/min时轴承外圈故障状态动力学响应

Fig.19 Dynamic response of bearings’ outer ring

表2 振动响应实验误差分析 (response)

Table 2 Experimental error analysis of vibration

工况转速	$f o 仿真$	$f o 实验$	相对误差	$f o 理论$	仿真误差	实验误差
r/min	Hz	Hz	%	Hz	%	%
600	55.20	53.71	2.70	55.25	0.09	2.79
1 200	109.50	106.20	3.01	110.50	0.90	3.89
1 500	136.10	131.84	3.13	138.13	1.47	4.56

表2 振动响应实验误差分析 (response)

Table 2 Experimental error analysis of vibration

工况转速	$f o 仿真$	$f o 实验$	相对误差	$f o 理论$	仿真误差	实验误差
r/min	Hz	Hz	%	Hz	%	%
600	55.20	53.71	2.70	55.25	0.09	2.79
1 200	109.50	106.20	3.01	110.50	0.90	3.89
1 500	136.10	131.84	3.13	138.13	1.47	4.56

参考文献 17

[1]	Li Y， Qiu L， Zhi Y J， et al. An overview of bearing voltages and currents in rail transportation traction motors［J］. Journal of Zhejiang University： Science， 2023， 24（3）： 226-242.
[2]	李小彭，曲兴超，李柏涛，等. 含轴电流损伤的球轴承动力学建模及特性分析［J］. 东北大学学报（自然科学版）， 2023， 44（10）： 1431-1439.
	Li Xiao-peng， Qu Xing-chao， Li Bai-tao， et al. Dynamic modeling and property analysis of ball bearings with shaft current damage［J］. Journal of Northeastern University （Natural Science）， 2023， 44（10）： 1431-1439.
[3]	Ma J J， Xue Y J， Han Q K， et al. Motor bearing damage induced by bearing current： a review［J］. Machines， 2022， 10（12）： 1167.
[4]	张轶东，张苗，赵博煊，等. 海上风电机组发电机轴承电腐蚀检测及原因分析［J］. 船舶工程， 2022， 44（sup1）： 106-110.
	Zhang Yi-dong， Zhang Miao， Zhao Bo-xuan， et al. Detection and cause analysis of electrical corrosion on generator bearings of offshore wind turbines［J］. Ship Engineering， 2022， 44（sup1）： 106-110.
[5]	温毅. 基于多模态流形的风力发电机轴承电流损伤识别与状态预测研究［D］. 湘潭：湖南科技大学， 2019.
	Wen Yi. Research on current damage identification and state prediction of wind turbine bearing based on multi-modal manifold［D］. Xiangtan： Hunan University of Science and Technology， 2019.
[6]	Prudhom A， Antonino-Daviu J， Razik H， et al. Time-frequency vibration analysis for the detection of motor damages caused by bearing currents［J］. Mechanical Systems and Signal Processing， 2017， 84： 747-762.
[7]	Liu Y Q， Chen Z G， Li W， et al. Dynamic analysis of traction motor in a locomotive considering surface waviness on races of a motor bearing［J］. Railway Engineering Science， 2021， 29（04）： 379-393.
[8]	Liu Y Q， Chen Z G， Zhai W M， et al. Dynamic investigation of traction motor bearing in a locomotive under excitation from track random geometry irregularity［J］. International Journal of Rail Transportation， 2022， 10（1）： 72-94.
[9]	Patra P， Saran V H， Harsha S P. Chaotic dynamics of cylindrical roller bearing supported by unbalanced rotor due to localized defects［J］. Journal of Vibration and Control， 2020， 26（21/22）： 1898-1908.
[10]	Niu L K， Cao H R， Hou H P， et al. Experimental observations and dynamic modeling of vibration characteristics of a cylindrical roller bearing with roller defects［J］. Mechanical Systems and Signal Processing， 2020， 138： 106553.
[11]	Cao H R， Su S M， Jing X， et al. Vibration mechanism analysis for cylindrical roller bearings with single/multi defects and compound faults［J］. Mechanical Systems and Signal Processing， 2020， 144： 106903.
[12]	Shi Z F， Liu J. An improved planar dynamic model for vibration analysis of a cylindrical roller bearing［J］. Mechanism and Machine Theory， 2020， 153： 103994.
[13]	Wang F T， Jing M Q， Yi J， et al. Dynamic modelling for vibration analysis of a cylindrical roller bearing due to localized defects on raceways［J］. Proceedings of the Institution of Mechanical Engineers， Part K： Journal of Multi-body Dynamics， 2015， 229（1）： 39-64.
[14]	Mattar A H A， Sayed H， Younes Y K， et al. Experimental verification and nonlinear dynamic response analysis of a rolling element bearing with localized defects［J］. Journal of Failure Analysis and Prevention， 2022， 22（4）： 1753-1770.
[15]	刘静. 滚动轴承缺陷非线性激励机理与建模研究［D］. 重庆：重庆大学， 2014.
	Liu Jing. Nonlinear vibration mechanisms and modeling of defects in rolling element bearings［D］. Chongqing： Chongqing University， 2014.
[16]	Patel V N， Tandon N， Pandey R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races［J］. Journal of Tribology， 2010， 132（4）： 041101.
[17]	Randall R B， Antoni J. Rolling element bearing diagnostics： a tutorial［J］. Mechanical Systems and Signal Processing， 2011， 25（2）： 485-520.